算法——二分查找

---

👇作者其它专栏

《数据结构与算法》《算法》《C++起始之路》

---

二分查找相关题解

1.二分查找

算法思路：

a.定义left，right指针，分别指向数组的左右区间。

b.找到待查找区间的中间点mid，找到后分三种情况讨论：

i.arr[mid]==target说明正好找到，返回mid的值；

ii.arr[mid]>target说明[mid,right]这段区间都是大于target的，因此舍去右边区间，在左边[left,mid-1]的区间继续查找，即让right=mid-1，然后重复b过程；

iii.arr[mid]<target说明[left,mid]这段区间的值都是小于target的，因此舍去左边区间，在右边区间[mid+1,right]区间继续查找，即让left=mid+1，然后重复b过程；

c.当left与right错开时，说明整个区间都没有这个数，返回-1。

//法一：遍历
//法二：二分查找
class Solution {
public:
    int search(vector<int>& nums, int target) {
        int left=0,right=nums.size()-1;
        while(left<=right){
            //int mid=(left+right)/2;可能会溢出
            int mid=left+(right-left)/2;
            if(nums[mid]<target) left=mid+1;
            else if(nums[mid]>target) right=mid-1;
            else return mid;
        }
        return -1;
    }
};

2.在排序数组中查找元素的第一个和最后一个位置

算法思路：

用的还是二分思想，就是根据数据的性质，在某种判断条件下将区间一分为二，然后舍去其中一个区间，然后在另一个区间内查找。

以下用x表示该元素，resLeft表示左边界，resRight表示右边界。

寻找左边界思路：

●寻找左边界：

●可以注意到一左边界划分的的两个区间的特点：

▢左边区间[left，resLeft-1]都是小于x的；

▢右边区间（包括左边界）[resLeft,right]都是大于等于x的；

●因此，关于mid的落点，我们可以分为以下两种情况：

●当我们的mid落在[left,resLeft-1]区间时，即arr[mid]<target。说明[left,mid]都是可以舍去的，此时更新left到mid+1的位置，继续在[mid+1,right]上寻找左边界；

●当mid落在[resLeft,right]的区间的时候，也就是arr[mid]>=target。说明[mid+1,right]（因为mid可能是最终结果，不能舍去）是可以舍去的，此时更新right到mid的位置，继续在[left,mid]上寻找左边界；

●由此，就可以通过二分，来快速寻找左边界；

注意：这里找中间元素需要向下取整。

因为后续移动左右指针时：

●左指针：left=mid+1，是会向后移动的，因此区间数会缩小的；

●右指针：right=mid，可能会原地踏步（如：若向上取整，如果剩下两个元素，left==1，right==2，mid==2。更新区间后，left，right，mid的值没有改变，就会陷入死循环）。

因此一定要注意，当right==mid时，要向下取整。

寻找右边界思路：

●寻找右边界：

●用resRight表示右边界；

●我们注意到右边界的特点：

▢左边区间（包括右边界）[left,resRight]都是小于等于x的；

▢右边区间[resRight+1,right]都是大于x的；

●因此，关于mid的落点，我们可以分为下面两种情况：

●当我们的mid落在[left,resRight]区间时，说明[left,mid-1]（mid不可以舍去，因为可能是最终结果）都是可以舍去的，此时更新left到mid的位置；

●当mid落在[resRight+1,right]的区间的时候，说明[mid,resRight]内元素是可以舍去的，此时更新right到mid-1位置；

●由此，就可以通过二分，来快速寻找右边界；

注意：这里找中间元素需要向上取整。

因为后续移动左右指针的时候：

●左指针：left=mid，可能会原地踏步（如：若向下取整，如果剩下1，2两个元素，left==1，right==2，mdi==1。更新区间之后，left，right，mid的值没有改变，就会陷入死循环）。

右指针：right=mid-1，是会向前移动的，因此区间是会缩小的；

因此一定要注意，当right=mid-1时，要向上取整。

二分查找算法总结：

1.关于什么时候用三段式，还是二段式中的某一个，一定不要强行去用，而是通过具体的问题分析情况，根据查找区间的变化确定指针的转移过程，从而选择一个模板。

2.当选择两段式的模板时：

●在求mid时，只有right-1的情况下，才会向上取整（即+1，取中间数时）

class Solution {
public:
    vector<int> searchRange(vector<int>& nums, int target) {
        //数组为空时
        if(nums.size()==0) return {-1,-1};
        int begin=0;
        int left=0,right=nums.size()-1;
        //求区间左端点
        while(left<right){
            int mid=left+(right-left)/2;
            if(nums[mid]<target) left=mid+1;
            else right=mid;
        }
        if(nums[left]!=target) return {-1,-1};
        else begin=left;
        //求区间右端点
        left=0,right=nums.size()-1;
        //left没必要重新置为0，因为它查找左端点后，一定不会超过右端点
        while(left<right){
            int mid=left+(right-left+1)/2;
            if(nums[mid]<=target) left=mid;
            else right=mid-1;
        }
        return {begin,right};
    }
};

3.搜索插入位置

算法思路：

a.分析插入位置左右两侧区间上元素的特点：

设插入位置的坐标为index，根据插入位置的特点可以知道：

●[left,index-1]内的所有元素均是小于target的；

●[index,right]内的所有元素均是大于等于target的；

b.设left为本轮查询的左边界，right为本轮查询的右边界。根据mid位置元素的信息，分析下一轮查询的区间：

●当nums[mid]>=target时，说明mid落在了[index,right]区间上，mid左边包括mid本身，可能是最终结果，所以我们接下来查找的区间在[left,mid]上。因此，更新right到mid位置，继续查找。

●当nums[mid]<target时，说明mid落在了[left,index-1]区间上，mid右边但不包括mid本身，可能是最终结果，索引我们接下来查找的区间[mid+1,right]上。因此，更新left到mid+1位置，继续查找。

c.直到我们的查找区间长度变为1，即left==right时，left或right所在的位置就是我们要找的结果。

class Solution {
public:
    int searchInsert(vector<int>& nums, int target) {
        int left=0,right=nums.size();
        while(left<right){
            int mid=left+(right-left)/2;
            if(nums[mid]<target) left=mid+1;
            else right=mid;
        }
        return left;
    }
};

4.x 的平方根

算法思路一（暴力）：

依次枚举【0，x】之间的所有数i：（这里没有必要研究是否枚举到x/2还是x/2+1。因为我们找到结果之后直接就返回了，往后的情况就不会再判断。反而研究枚举空间，既 耽误时间，又可能出错）

●若i*i==x，直接返回x；

●若i*i>x，说明之前的一个数是结果，返回i-1

由于i*i可能超过int的最大值，因此使用long long类型

class Solution{
public:
    int mySqrt(int x){
        //防止溢出
        long long i=0;
        for(i=0;i<=x;i++){
            if(i*i==x) return i;
            if(i*i>x) return i-1;
        }
        return -1;
    }
};

算法思路二（二分）：

设x的平方根的最终结果为index：

a.分析index左右两次数据的特点：

●【0，index】之间的元素平方后都是小于等于x的；

●【index+1，x】之间的元素，平方后都是大于x的。

由此可以使用二分查找算法

//法一：循环遍历，平法大于x，即找到（此数-1）
//法二：二分
class Solution {
public:
    int mySqrt(int x) {
        //可将区间分为小于等于x的 大于x的
        int left=1,right=x;
        if(x<1) return 0;
        while(left<right){
            //long long 防止溢出
            long long mid=left+(right-left+1)/2;
            if(mid*mid<=x) left=mid;
            else right=mid-1;
        }
        return left;
    }
};

5.山脉数组的峰顶索引

算法思路一（暴力）：

顶峰的特点：比两边的元素都要大。

因此，我们可以遍历数组内的每一个元素，找到某一个元素比两边的元素大即可。

class Solution {
public:
    int peakIndexInMountainArray(vector<int>& arr) {
        int n=arr.size();
        //遍历数组内每一个元素，直到找到峰顶
        for(int i=1;i<n-1;i++){
            //峰顶满足条件
            if(arr[i]>arr[i-1]&&arr[i]>arr[i+1])    
                return i;
        }
        return -1;
    }
};

算法思路二（二分）：

1.分析峰顶位置的数据特点，以及山峰两旁的数据的特点：

●峰顶数据特点：arr[i]>arr[i-1]&&arr[i]>arr[i+1];

●峰顶左边的数据特点：arr[i]>arr[i-1]&&arr[i]<arr[i+1],即呈上升趋势；

●峰顶右边数据的特点：arr[i]<ar[i-1]&&arr[i]>arr[i+1],即呈下降趋势。

2.因此，根据mid位置的信息，我们可以分为下面三种情况：

●若mid位置呈上升趋势，说明我们接下来要在【mid+1，right】区间继续搜索；

●若mid位置呈下降趋势，说明我们接下来要在【left，mid-1】区间搜索；

●若mid位置就是山峰，直接返回结果。

class Solution {
public:
    int peakIndexInMountainArray(vector<int>& arr) {
        //峰顶一定不会位于首尾
        int left=1,right=arr.size()-2;
        while(left<right){
            int mid=left+(right-left+1)/2;
            if(arr[mid]>arr[mid-1]) left=mid;
            else right=mid-1;
        }
        return left;
    }
};

6.寻找峰值

解法思路（二分）：

寻找二段性：

任取一点i，与下一个点i+1，会有如下两种情况：

●arr[i]>arr[i+1]:此时【左侧区域】一定会存在山峰（因为最左侧是负无穷），那么我们可以取左侧寻找结果；

●arr[i]<arr[i+1]：此时【右侧区域】一定会存在山峰（因为最右侧是负无穷），那么我们可以取右侧寻找结果。

当我们找到【二段性】时，就可以尝试用【二分查找】算法解决问题。

//法一：从前向后遍历，分情况讨论
//法二：二分
class Solution {
public:
    //3种情况，1一直递减；2一直递增；3有增有减
    int findPeakElement(vector<int>& nums) {
        int left=0,right=nums.size()-1;
        while(left<right){
            int mid=left+(right-left)/2;
            //左边一定存在峰值，右边不一定[左边] [右边]
            if(nums[mid]<nums[mid+1]) left=mid+1;
            //右边一定存在峰值，左边不一定
            else right=mid;
        }
        return left;
    }
};

7.寻找旋转排序数组中的最小值

算法思路（二分）：

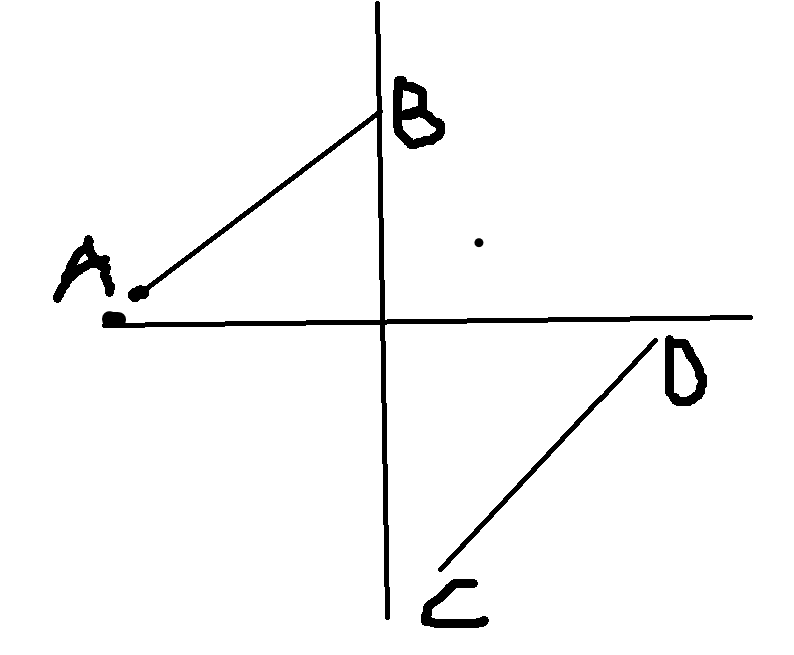
c点就是我们要求的点。

二分的本质：找到一个判断标准，使得查找区间能够一分为二。

通过图像我们可以发现，【A，B】区间内的点都是严格大于D点的值的，C点的值是严格小于D的点的值的。但是当【C，D】区间只有一个元素的时候，C点的值是可能等于D点的值的。

因此，初始化左右两个指针left，right：

然后根据mid的落点，我们可以这样划分下一次查询的区间：

●当mid在【A，B】区间的时候，也就是mid位置的值严格大于D点的值，下一次查询区间在【mid+1，right】上；

●当mid在【C，D】区间的时候，也就是mid位置的值严格小于等于D点的值，下次查询区间在【left，mid】上。

当区间长度变成1的时候，就是我们要找的结果。

class Solution {
public:
    int findMin(vector<int>& nums) {
        int left=0,right=nums.size()-1;
        int x=nums[right];
        while(left<right){
            int mid=left+(right-left)/2;
            //与数组中最后一个值比较
            if(nums[mid]>x) left=mid+1;
            else right=mid;
        }
        return nums[left];
    }
};

也可以用左侧为基准值，但要注意排除数组为升序的情况：

class Solution {
public:
    int findMin(vector<int>& nums) {
        int left=0,right=nums.size()-1;
        int x=nums[left];//以左端点为基准值
        if(x<nums[right]) return nums[left];
        while(left<right){
            int mid=left+(right-left)/2;
            if(nums[mid]>=x) left=mid+1;//此时左端点一定不是最小值
            else right=mid;
        }
        return nums[left];
    }
};

8.点名

算法思路（二分）：

在这个升序的数组中，我们发现：

●在第一个缺失位置的左边，数组内的元素都是与数组的下标相等的；

●在第一个缺失位置的右边，数组内的元素与数组下标是不相等的。

因此，我们可以利用这个【二段性】，来使用【二分查找】算法。

//法一：直接遍历 法二：桶思想 法三：位运算（异或） 法四：数学公式（高斯）
//法五：二分
class Solution {
public:
    int takeAttendance(vector<int>& records) {
        int left=0,right=records.size()-1;
        while(left<right){
            int mid=left+(right-left)/2;
            if(mid==records[mid]) left=mid+1;
            else right=mid;
        }
        //防止缺失的是最后一个数字
        if(left==records[left]) return left+1;
        return left;
    }
};