动态规划介绍
++动态规划(dynamic programming)++是一个重要的算法范式,它将一个问题分解为一系列更小的子问题,并通过存储子问题的解来避免重复计算,从而大幅提升时间效率。
我们可以通过不断地缩减问题的规模,通过子问题的解找出原问题的解,就像慢慢将小水珠收集起来,让它汇聚成小河,最后在汇聚为大海
其适用于解最优化的问题,一般可以用以下步骤来设计动态规划算法
1)找出最优解的性质,刻画最优解的结构
2)递归的定义最优值
3)自底向上的方式计算出最优值
4)根据计算最优值时得到的信息构造最优解
下面让我们来看看一些经典的问题:
最大连续子序列之和
给定数组AR=[−2,11,−4,13,−5,−2]求其连续子序列的最大和
根据这个题目我们很容易想到穷举这个策略,通过枚举所有的子序列之和然后得出结果
cpp
void MaxLeng(int* ar,int n)
{
if (ar == NULL || n < 1)
{
return;
}
int max = ar[0];
for (int i = 0; i < n; i++)//确定数组的开头
{
for (int j = i; j < n; j++)//确定数组的结尾
{
int num = 0;
for (int k = i; k <= j; k++)//计算出任意子序列之和
{
num += ar[k];
}
if (max < num)
{
max = num;
}
}
}
printf("The MaxLeng is %d", max);
}但是我们发现这样三层循环时间复杂度为 O(n3),效率极低
这时我们可以使用动态规划来瞧一瞧,
我们先规定一个dp数组,dp[ar,i]这个数组表示的时ar数组从0到i之间的最大子序列之和,我们可以发现,dp[ar,i] = (dp[ar,i-1] + arr[i] ? 0)
cpp
void PrintAR(int *AR,int n)
{
if (NULL == AR || n < 1) return;
for (int i = 0; i < n; i++)
{
printf("%5d" ,AR[i]);
}
printf("\n");
}//打印函数
int MaxLeng1(int* ar,int n)
{
if (ar == NULL || n < 1)
{
return 0;
}
if (n == 1)
{
return ar[0] > 0 ? ar[0] : 0;
}
int* curMax = (int*)calloc(n, sizeof(int));//创建dp数组
curMax[0] = ar[0];
for (int i = 1; i < n; ++i)
{
curMax[i] = max(0, curMax[i - 1] )+ ar[i];//如果是负数则跳过直到遇到第一个正数
}
PrintAR(curMax, n);
return 0;
}
int main(){
int AR[] = {-2, 11, -4, 13, -5, -2 };
int n = sizeof(AR) / sizeof(AR[0]);
PrintAR(AR, n);
MaxLeng1(AR,n);
return 0;
} 我们可以看到结果如下:其中上面的数组为原数组,下面的为我的dp数组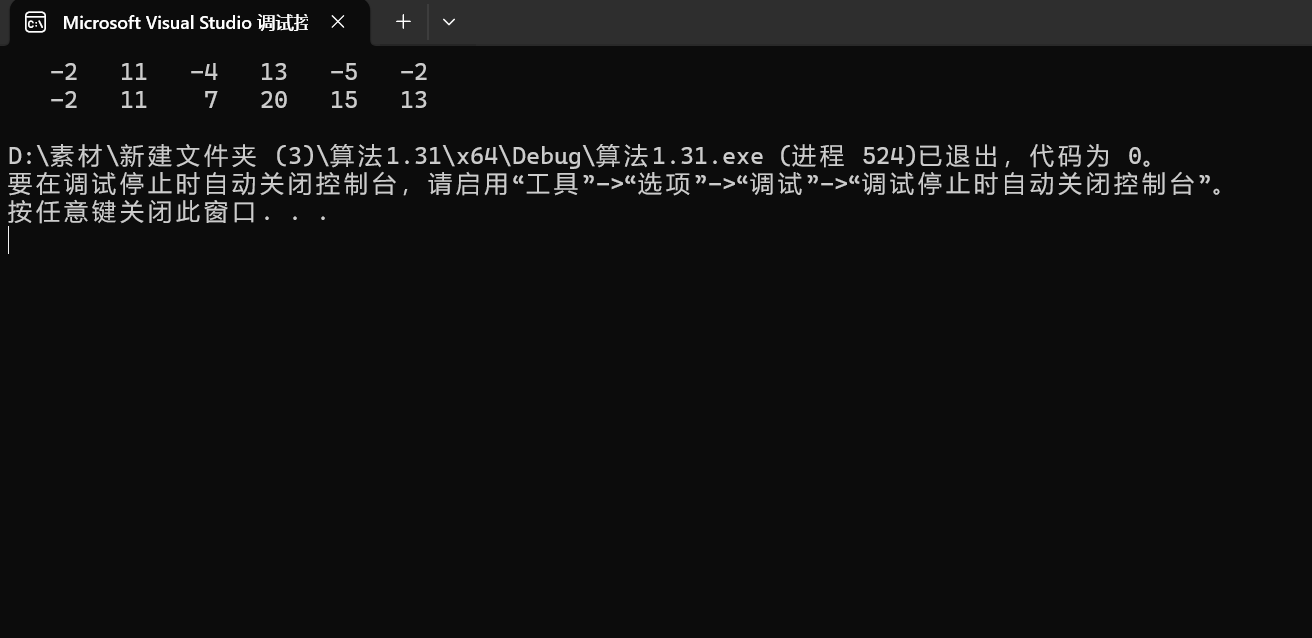
最长公共子序列
题目描述
给定两个字符串
s1和s2,编写一个程序或算法,找出它们的最长公共子序列(LCS)的长度。
abnf
s1 = "ABCBDAB"
s2 = "BDCABA"
首先假设有两个序列分别为
X = {x1,x2,x3,x4,x5...xm}
Y = {y1,y2,y3,y4,y5...yn}
他们的最长公共子序列为
Z={z1,z2,z3,z4,z5...zk}
通过观察我们可以得出
当x[m] == y[n] 时
zk 一定等于 x[m] or y[n]
当x[m] != y[n]并且x[m] != z[k]
zk就变成了x[m-1]与y[n]的最长公共子序列
当x[m] !=y[n] 且y[n] != z[k]
zk就成了x[m] 与 y[n-1]的最长公共子序列了
这时我们规定dp数组dp[i][j]表示其x数组中前i个与y数组中前j个的最长公共子序的长度,
我们很容易得知dp[0][j]和dp[i][0]都为0,因为任何序列和空序列的子序列都为空,再根据我们的动规方程
当x[i] == y[j]时,
dp[i][j] == dp[i-1][j-1] + 1
x[i] != y[j]时
dp[i][j] = max(dp[i-1][j],dp[i][j-1])
翻译后代码如下
cpp
int num=0;
int LCSLength(char* X,char* Y,const int i,const int j)
{
num+=1;
if (i == 0 || j == 0) return 0;
if (X[i] == Y[j]) return LCSLength(X, Y, i - 1, j - 1) + 1;
else return max(LCSLength(X, Y, i - 1, j), LCSLength(X, Y, i, j - 1));
}
int main(){
const int xm = 7;
const int yn = 6;
char X[xm+1] = { '#','A','B','C','B','D','A','B' };
char Y[yn+1] = { '#','B','D','C','A','B','A' };
printf ("%d \n",LCSLength(X, Y, xm, yn));
return 0;
} 优化
我们发现这样子的递归数量相当庞大,这是因为我们计算了重叠子问题,那么怎么优化我们的算法呢?
我们可以引入一个二维数组,通过这个二维数组记录每一个被访问过的值,如果其被访问过那么我们就不在继续访问
cpp
int num = 0;
int LCSLength(char* X, char* Y, const int i, const int j,
std::vector<std::vector<int>>& c)
{
num += 1;
if (i == 0 || j == 0) return 0;
else if (c[i][j] > 0) return c[i][j];//如果已经被记录则返回不进行运算
else if (X[i] == Y[j])
{
c[i][j] = LCSLength(X, Y, i - 1, j - 1, c) + 1;
}
else
{
int t1 = LCSLength(X, Y, i - 1, j, c);
int t2 = LCSLength(X, Y, i, j - 1, c);
if (t1 > t2)
{
c[i][j] = t1;
}
else
{
c[i][j] = t2;
}
}
return c[i][j];
}
int main()
{
const int xm = 7;
const int yn = 6;
char X[xm+1] = { '#','A','B','C','B','D','A','B' };
char Y[yn+1] = { '#','B','D','C','A','B','A' };
std::vector<std::vector<int>> c(xm + 1, std::vector<int>(yn + 1, 0));
printf ("%d \n",LCSLength(X, Y, xm, yn,c));
cout << num << endl;
Printf(xm,yn,c);
return 0;
} 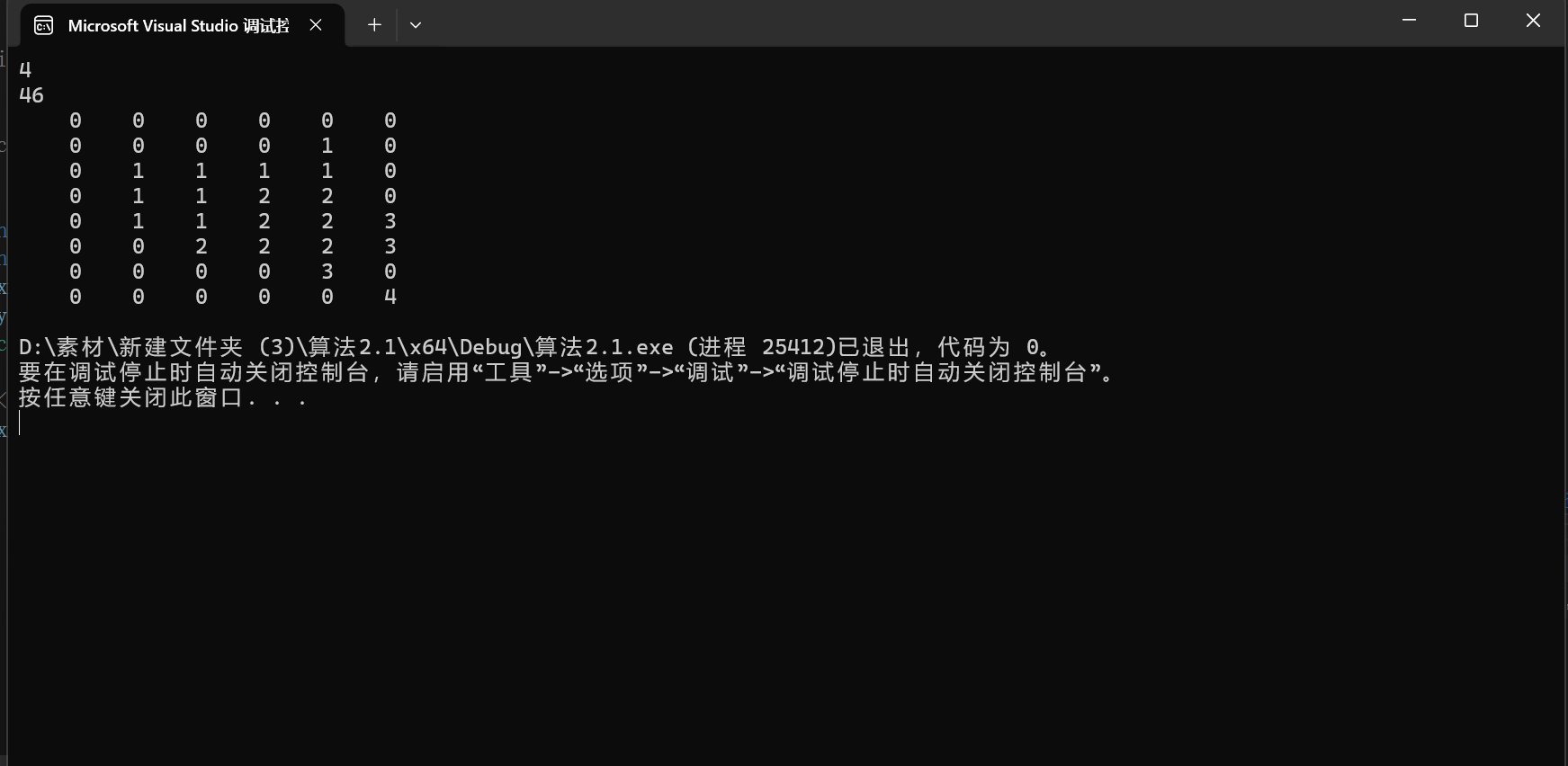
这样我们发现递归数量大大减少了
但是还有一个问题,我们发现我们只是知道了最长的公共子序列的长度,我们并不知道这个子序列是什么,那么如何才能打印出这个最长公共子序列呢?
这时我们就需要另一张表s来记录如果是x[i]==y[j]我们记为1
如果为行减一我们记为2
如果为列减一我们记为3
通过这个表来回溯我们所遍历的数组
cpp
int LCSLength(char* X, char* Y, const int i, const int j,
std::vector<std::vector<int>>& c, std::vector<std::vector<int>>& s)
{
num += 1;
if (i == 0 || j == 0) return 0;
else if (c[i][j] > 0) return c[i][j];
else if (X[i] == Y[j])
{
c[i][j] = LCSLength(X, Y, i - 1, j - 1, c,s) + 1;
s[i][j] = 1;
}
else {
int t1 = LCSLength(X, Y, i - 1, j, c,s);
int t2 = LCSLength(X, Y, i, j - 1, c,s);
if (t1 > t2)
{
c[i][j] = t1;
s[i][j] = 2;
}
else
{
c[i][j] = t2;
s[i][j] = 3;
}
}
return c[i][j];
}
void LCS(char* X,int i ,int j, std::vector<std::vector<int>>& s)//回溯
{
if (i == 0 || j == 0) return;
if (s[i][j] == 1)
{
LCS(X,i-1,j-1,s);
printf("%5c", X[i]);
}
else if (s[i][j] == 2)
{
LCS(X, i - 1, j, s);
}
else
{
LCS(X, i, j - 1, s);
}
}
int main(){
const int xm = 7;
const int yn = 6;
char X[xm+1] = { '#','A','B','C','B','D','A','B' };
char Y[yn+1] = { '#','B','D','C','A','B','A' };
std::vector<std::vector<int>> c(xm + 1, std::vector<int>(yn + 1, 0));
std::vector<std::vector<int>> s(xm + 1, std::vector<int>(yn + 1, 0));
printf ("%d \n",LCSLength(X, Y, xm, yn,c,s));
cout << num << endl;
printf("c[i][j] \n");
Prinf(xm, yn, c);
printf("\n");
printf("s[i][j] \n");
Prinf(xm, yn, s);
printf("LCS is \n");
LCS(X,xm,yn,s);
return 0;
} 结果如下:
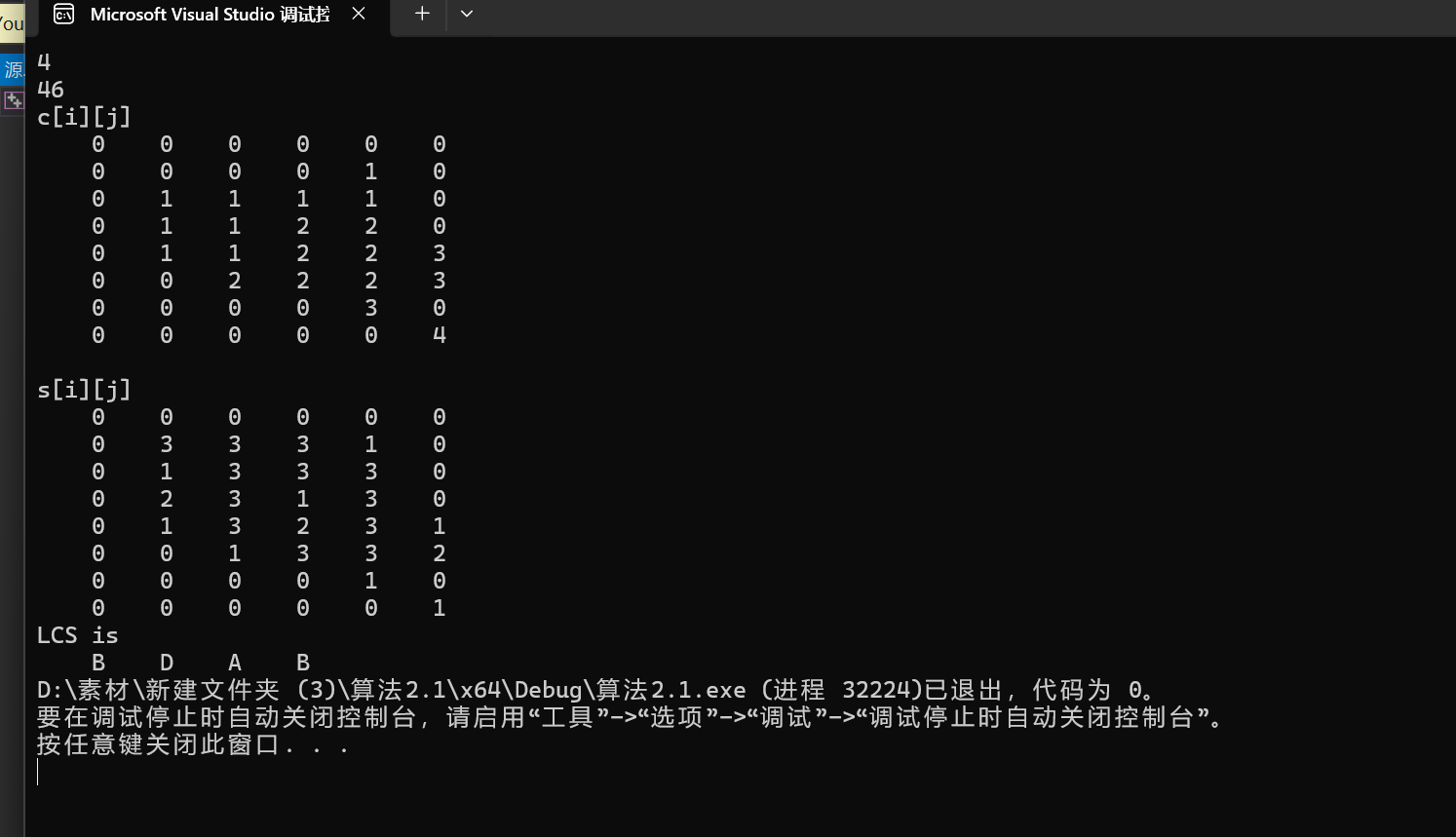
打家劫舍
题目描述:
假设你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响偷窃的唯一限制是相邻的房屋装有相互连通的防盗系统。如果两间相邻的房屋在同一晚被闯入,系统会自动报警。给定一个代表每个房屋存放金额的非负整数数组,计算在不触动警报的情况下,能够偷窃到的最高金额。
通过分析题目我们可以知道,假设dp数组存放了已经取得的最大值,那么我们发现
dp[i] = max(dp[i-1],dp[i-2]+ar[i])
这意味着如果我们要打劫第i家,就不能打劫低i-1家,所以现在的最大值是我们第i家与前i-2家的最大值之和,
cpp
int Rob(std::vector<int>& ar)
{
int n = ar.size();
if (n == 0) return 0;
if (n == 1) return ar[0];
vector<int> dp(n + 1, 0);
dp[0] = ar[0];
for (int i = 2; i <= n; i++)
{
dp[i] = max(dp[i - 1], dp[i - 2] + ar[i - 1]);
}
return dp[n];
}寻找最长上升子序列
题目描述:
给定一个无序的整数数组,要求找到其中最长的上升子序数组,返回其长度
那么如何利用动态规划来解决这个问题呢?
我们规定dp[i]存储前i个的最长升序列的最大数,我们要找到ar[i] 前面有多少个增序列,我们可以用两个循环来表示,外层循环表示当前的值,内层循环来寻找我们的最大序列
cpp
int AsOrder(std::vector<int> ar)
{
int n = ar.size();
if (n == 0)
{
return 0;
}
if (n == 1)
{
return 1;
}
std::vector<int> dp(n + 1, 1);
int max1 = 1;
for (int i = 0; i < n; i++)
{
for (int j = 0; j < i; j++)
{
if (ar[i] > ar[j])
{
dp[i] = max(dp[j] + 1, dp[i]);//如果发现i 大于j 去寻找 j的最大序列
}
if(dp[i] > dp[max1])
{
max1 = i;
}
}
}
return dp[max1];
}0-1背包问题
0-1背包问题是一种经典的动态规划问题。给定一组物品,每个物品有重量和价值,在背包容量限制下选择物品装入背包,目标是使背包中物品的总价值最大。每个物品只能选择装入(1)或不装入(0)
对于这个问题,我们需要明白原问题的解为:
sum(Wi)<C,
&&
Max(Vi)
如果我们发现当第i个物品它是最后一个物品时,我们看背包剩余容量看是否可以装下,
当他不是最后一个物品时,我们先看看他能否装下,然后比较装与不装的大小,返回最大的那个就可以算出来最大值
cpp
int kanpSack(const int* W,
const int* V, int i, int j, int n)
//i代表当前的个数,j代表背包当前可以承受的重量,n代表物品个数
{
if (i == n)
{
return j > W[i] ? V[i] : 0;
}
else if(j<W[i])
{
return kanpSack(W, V, i + 1, j, n);
}
else
{
int t1 = kanpSack(W, V, i + 1, j - W[i], n) + V[i];//装i;
int t2 = kanpSack(W, V, i + 1, j , n);//不装i
if (t1 > t2) return t1;
else return t2;
}
}那么我们如何进行优化呢,其实我们发现,这个的短板和我们之前谈论过的最长公共子序列的问题很像,都是因为我们产生了许多重复计算,
cpp
int kanpSack(const int* W,
const int* V, int i, int j, int n,std::vector<std::vector<int>>& m)//这里传进来的时m的引用
//i代表当前的个数,j代表背包当前可以承受的重量,n代表物品个数
{
if (i == n)
{
return j > W[i] ? V[i] : 0;
}
else if(m[i][j] > 0)
{
m[i][j] = anpSack(W, V, i + 1, j, n,m)
}
else if(j<W[i])
{
m[i][j] kanpSack(W, V, i + 1, j, n,m);
}
else
{
int t1 = kanpSack(W, V, i + 1, j - W[i], n) + V[i];//装i;
int t2 = kanpSack(W, V, i + 1, j , n);//不装i
m[i][j] = t1 > t2 ? t1:t2;
}
return m[i][j];
}这次的优化还是我们引入了数组m,让其记录我们每一次计算的结果,在递归计算的时候如果发现我们已经计算过后就不在计算,这样就可以极大的减少重复问题的计算.
矩阵的连乘问题
问题描述:
给定n个矩阵{A₁, A₂, ..., Aₙ},其中矩阵Aᵢ的维度为pᵢ₋₁ × pᵢ(即Aᵢ的行数为pᵢ₋₁,列数为pᵢ)。矩阵连乘问题需要找到一个最优的括号化方案,使得计算A₁A₂...Aₙ所需的标量乘法次数最少。
矩阵连乘问题通常使用动态规划解决。定义一个二维数组m[i][j]表示计算Aᵢ到Aⱼ的最小乘法次数,递推公式为:
m[i][j] = min(m[i][k] + m[k+1][j] + pᵢ₋₁ × pₖ × pⱼ) for i ≤ k < j
初始化条件为m[i][i] = 0,表示单个矩阵无需乘法。