【UWB与IMU紧耦合定位，MATLAB例程】UWB的TOA定位方法，与IMU紧耦合，对目标轨迹定位并输出误差统计。适用于二维平面的高精度定位导航

二维平面下的 UWB 与 IMU 紧耦合定位导航系统仿真框架 ，采用扩展卡尔曼滤波（EKF）进行多源信息融合，采集的是IMU的加速度、角速度，UWB的TOA的距离信息
原创代码，禁止翻卖

文章目录

程序详解
系统结构示意
运行结果
MATLAB源代码

程序详解

该程序构建了一个二维平面下的 UWB 与 IMU 紧耦合定位导航系统仿真框架，采用扩展卡尔曼滤波（EKF）进行多源信息融合，实现：

IMU高频惯性推算（100 Hz）
UWB低频距离观测修正（10 Hz）
紧耦合状态估计
误差统计与性能评估

系统属于基于测距的非线性融合定位模型，典型应用场景包括室内定位、GNSS拒止环境下的移动机器人导航等。

系统结构示意

系统由三部分构成：

IMU模块
- 输出加速度
- 输出角速度
UWB模块
- 多锚点距离观测
- 非线性测距模型
EKF紧耦合融合模块
- 预测：惯性积分模型
- 更新：距离观测修正

紧耦合特征说明

该程序属于紧耦合（Tightly Coupled）融合结构，原因：

EKF直接使用原始距离观测
未先进行UWB独立定位
状态由单一滤波器统一估计

对比松耦合：

类型	处理方式
松耦合	UWB先解算位置，再融合
紧耦合	直接融合原始距离观测

仿真设置

仿真时长：20 s
IMU频率：100 Hz
UWB频率：10 Hz
锚点数量：5个
轨迹类型：
- 前10秒：圆周运动
- 后10秒：直线运动

这种轨迹组合用于验证：

曲线运动收敛性
直线段稳定性
观测缺失情况下的误差增长趋势

误差分析指标

程序输出：

位置RMSE
最大误差
平均误差
标准差

并绘制：

轨迹对比图
分量误差曲线
位置误差范数

运行结果

轨迹图示：

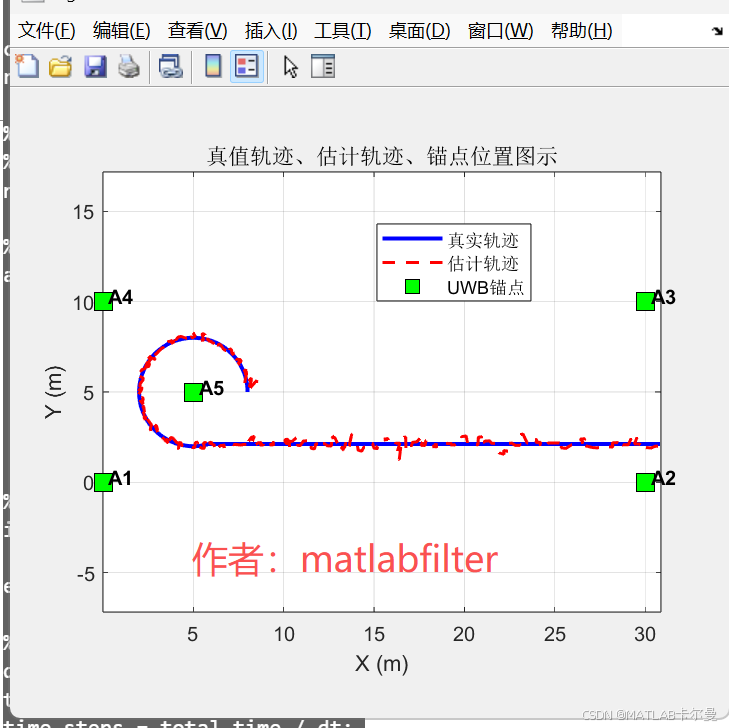
位移曲线：

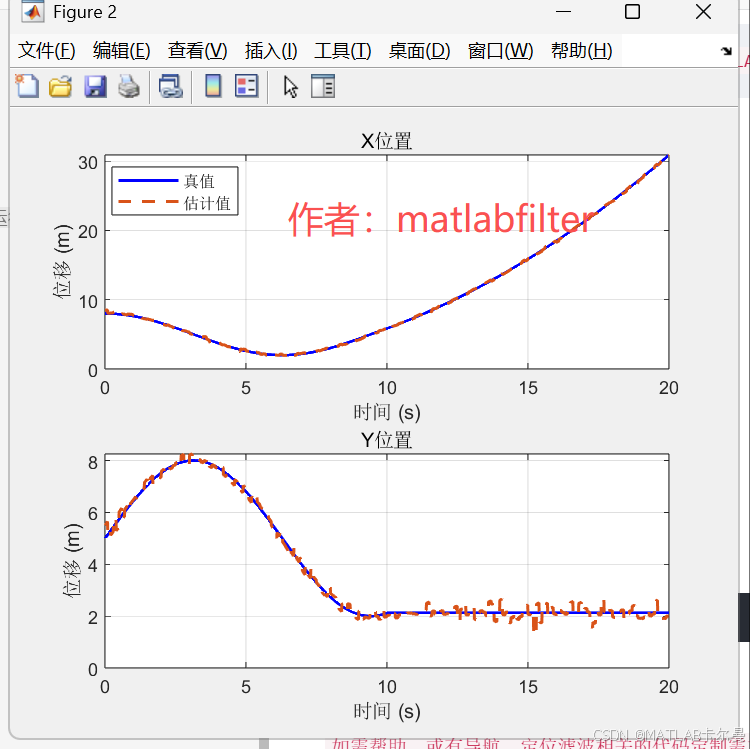
位置误差曲线：

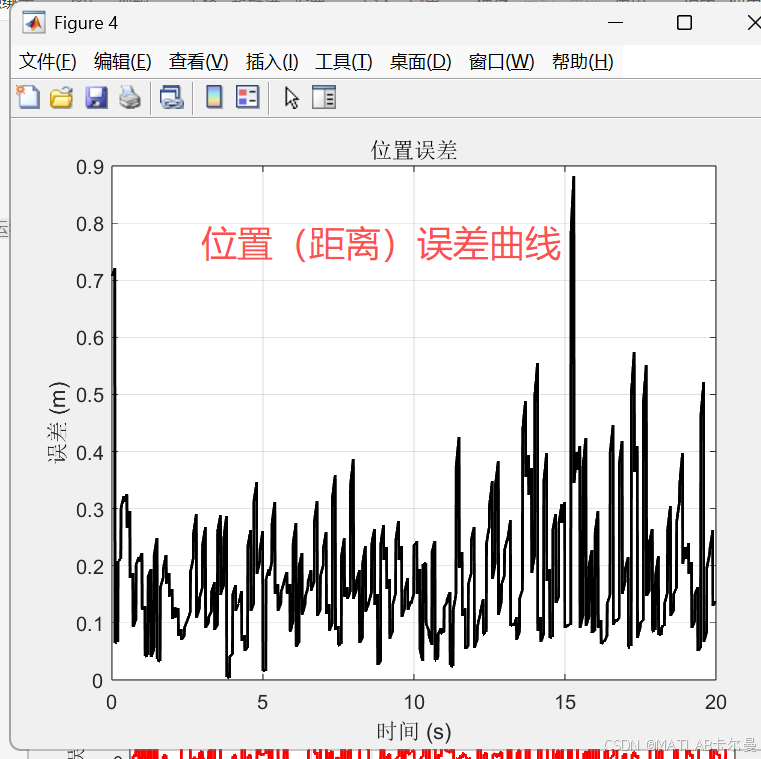
命令行输出的结果：

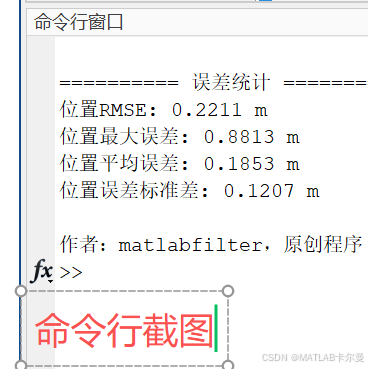
MATLAB源代码

完整代码如下：

matlab 复制代码

%% UWB与IMU紧耦合定位导航系统，EKF做紧耦合，
% 作者：matlabfilter
% 2026-02-13/Ver1

clear; close all; clc;
rng(0);

%% ===参数初始化 ===
% 锚点数量（可修改，下方坐标的行数同步修改）
num_anchors = 5;

% UWB锚点坐标 [x, y] (每个锚点一行，先X和Y坐标)
anchor_positions = [
    0,   0;      % 锚点1
    30,  0;      % 锚点2
    30,  10;     % 锚点3
    0,   10;     % 锚点4
    5,   5       % 锚点5
    ];

% 确保锚点数量与坐标匹配
if size(anchor_positions, 1) ~= num_anchors
    error('锚点数量与坐标不匹配');
end

% 仿真参数
dt = 0.01;              % 时间步长 (s)
total_time = 20;        % 总仿真时间 (s)
time_steps = total_time / dt;

% 噪声参数
imu_acc_noise = 0.1;        % IMU加速度噪声标准差 (m/s^2)
imu_gyro_noise = 0.1;      % IMU角速度噪声标准差 (rad/s)
uwb_range_noise = 0.2;      % UWB测距噪声标准差 (m)

%% == 生成真实轨迹
% 圆形+直线组合轨迹（可修改为其他轨迹）
t = 0:dt:total_time-dt;
true_trajectory = generate_trajectory(t);
true_trajectory.theta(true_trajectory.theta > pi) = true_trajectory.theta(true_trajectory.theta > pi) - 2*pi;

代码获取：

如有一对一讲解或代码定制需求，请点击下方卡片联系作者