本文首发于洛谷平台,CSDN 版本为转载。
6.7 二元铲雪
P3543 [POI 2012] WYR-Leveling Ground。
给出一个序列 h i h_i hi,一次操作将一个区间上的所有元素加上或减去 a a a,或者加上或减去 b b b。
要求操作过程中点权始终非负。求使得所有元素全变为 0 0 0 的最小操作数,或者报告无解。
n ≤ 10 5 n \le 10^5 n≤105,1 秒,125 MB。
:::::success[题解]
考虑每个数字一定是 a x + b y ax+by ax+by 的形式,由裴蜀定理先判掉无解。有解则将 a , b , h i a,b,h_i a,b,hi 都除掉 gcd ( a , b ) \gcd(a,b) gcd(a,b),显然不会影响答案。
考虑 2.1 的差分法,令 d i = h i − h i − 1 d_i=h_i-h_{i-1} di=hi−hi−1,特别地 d n + 1 = − h n d_{n+1}=-h_n dn+1=−hn。则题目转化为:
- 选择 i , j i,j i,j,令 d i ← d i + a , d j ← d j − a d_i \gets d_i+a, d_j \gets d_j -a di←di+a,dj←dj−a。
- 选择 i , j i,j i,j,令 d i ← d i + b , d j ← d j − b d_i \gets d_i+b,d_j \gets d_j-b di←di+b,dj←dj−b。
- 目标为 ∀ 1 ≤ i ≤ n + 1 , d i = 0 \forall 1 \le i \le n+1, d_i=0 ∀1≤i≤n+1,di=0。
下文令 n ← n + 1 n \gets n +1 n←n+1。
对于 d i d_i di,设我们在该位置进行了 x i x_i xi 次 + a +a +a, y i y_i yi 次 + b +b +b,负数次操作的意义则为区间减。可以列出方程:
a x i + b y i = − d i ax_i+by_i=-d_i axi+byi=−di
容易用 exGCD 求得 a x + b y = gcd ( a , b ) ax+by=\gcd(a,b) ax+by=gcd(a,b) 的一组特解 x 0 , y 0 x_0,y_0 x0,y0,进而得到通解形式:
x i = x 0 + k × b d i x_i=x_0+k \times \dfrac{b}{d_i} xi=x0+k×dib
y i = y 0 − k × a d i y_i=y_0-k \times \dfrac{a}{d_i} yi=y0−k×dia
2.1 的结论告诉我们,全局操作次数为
1 2 ∑ i = 1 n ( ∣ x i ∣ + ∣ y i ∣ ) \dfrac{1}{2} \sum_{i=1}^n \left( |x_i|+|y_i| \right) 21i=1∑n(∣xi∣+∣yi∣)
现在我们重新表述题目:
- 找到一组 x i , y i x_i,y_i xi,yi 满足:
- x i = x 0 + k × b d i x_i=x_0+k \times \dfrac{b}{d_i} xi=x0+k×dib。
- y i = y 0 − k × a d i y_i=y_0-k \times \dfrac{a}{d_i} yi=y0−k×dia
- ∑ i = 1 n x i = 0 \sum \limits_{i=1}^n x_i=0 i=1∑nxi=0。这等价于 ∑ i = 1 n y i = 0 \sum \limits_{i=1}^n y_i=0 i=1∑nyi=0。
- 在此基础上,最小化 1 2 ∑ i = 1 n ( ∣ x i ∣ + ∣ y i ∣ ) \dfrac{1}{2} \sum \limits_{i=1}^n \left( |x_i|+|y_i| \right) 21i=1∑n(∣xi∣+∣yi∣)。
注意到代价变化量
F ( i ) = ∣ x 0 + i b ∣ − ∣ y 0 − i a ∣ F(i)=|x_0+ib|-|y_0-ia| F(i)=∣x0+ib∣−∣y0−ia∣
是一个分段线性函数,左端单调减,右端单调增,中间段单调减或者单调增。
下图展示了 x 0 = − 3 , y 0 = 3 , a = 2 , b = − 1 x_0=-3,y_0=3,a=2,b=-1 x0=−3,y0=3,a=2,b=−1 时的情形。
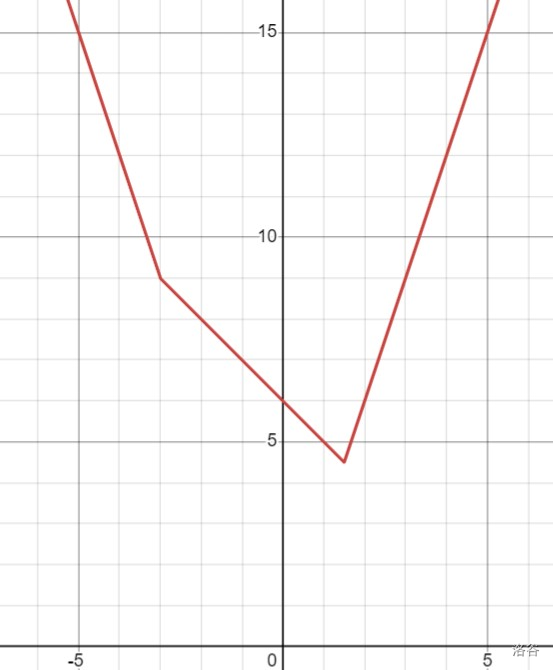
忽略第三条限制,把 x i , y i x_i,y_i xi,yi 取到谷点,这样代价自然最小。注意到代价关于调整距离的函数应当具有凸性,可以用神奇调整法使得 ∑ i = 1 n x i = 0 \sum \limits_{i=1}^n x_i=0 i=1∑nxi=0。
设当前位置为 p i p_i pi。每次对 p i p_i pi 做一次调整, x i x_i xi 都会移动 b b b 个单位。故总调整次数为 1 b ∣ ∑ i = 1 n x i ∣ \dfrac{1}{b}\left| \sum \limits_{i=1}^n x_i \right| b1 i=1∑nxi 。
因为斜率分 O ( 1 ) O(1) O(1) 段,我们可以用一个 vector 存下每种决策。具体地,记录二元组 ( w i , s i ) (w_i,s_i) (wi,si) 表示以代价 w i w_i wi 移动 s i s_i si 步。按 w i w_i wi 排序,顺次取就是正确的。
压力给到如何求 ( w i , s i ) (w_i,s_i) (wi,si)。设 D ( i ) = F ( i ± 1 ) − F ( i ) D(i)=F(i \pm 1)-F(i) D(i)=F(i±1)−F(i),其中 ± \pm ± 的符号取决于调整的方向。
以向右调整为例,可以求出两个拐点 ⌊ − x i b ⌋ , ⌊ y i a ⌋ \left\lfloor -\dfrac{x_i}{b} \right\rfloor,\left\lfloor \dfrac{y_i}{a}\right\rfloor ⌊−bxi⌋,⌊ayi⌋。顺次遍历每个分界点,对分界点中间的段计算。
本题有一个神奇的性质:每轮调整只需调整一次。证明。
代码细节上,注意若干处需要 __int128。
cpp
const int N = 1e5 + 5;
int n, a, b, g, h[N], d[N];
void exgcd(int128 a, int128 b, int128& x, int128& y)
{b ? (exgcd(b, a % b, y, x), y -= a / b * x) : (x = 1, y = 0);}
tuple<int128, int128, int128> info[N];
int128 _abs(int128 x) {return x >= 0 ? x : -x;}
void _main() {
cin >> n >> a >> b, g = gcd(a, b);
for (int i = 1; i <= n; i++) {
cin >> h[i];
if (h[i] % g) return cout << -1, void();
h[i] /= g;
}
for (int i = 1; i <= n + 1; i++) d[i] = h[i] - h[i - 1];
n++, a /= g, b /= g;
if (a < b) swap(a, b);
int128 x0, y0; exgcd(a, b, x0, y0);
int128 cost = 0, cur = 0;
auto work1 = [&]() -> void {
for (int i = 1; i <= n; i++) {
// x * a + y * b = -d[i]
int128 v = -d[i], x = (x0 * v % b + b) % b, y = (v - a * x) / b;
auto F = [&](int i) -> int128 {return _abs(x + i * b) + _abs(y - i * a);};
int128 p = y / a;
if (F(y / a - 1) < F(p)) p = y / a - 1;
if (F(y / a + 1) < F(p)) p = y / a + 1;
cost += F(p), cur += x + p * b;
info[i] = {x, y, p};
}
};
work1();
int offset = -(cur / b), dir = offset < 0 ? -1 : 1;
if (offset == 0) return cout << static_cast<u64>(cost / 2), void();
vector<pair<int128, int128>> vec;
auto work2 = [&]() -> void {
for (int i = 1; i <= n; i++) {
auto [x, y, p] = info[i];
auto F = [&](int i) -> int128 {return _abs(x + i * b) + _abs(y - i * a);};
auto D = [&](int i) -> int128 {return F(i + dir) - F(i);};
int p1 = floor(-1.0 * x / b), p2 = floor(1.0 * y / a);
if (dir == 1) {
int cur = p;
vector<int> tmp = {p1, p2};
sort(tmp.begin(), tmp.end());
for (int pos : tmp) {
if (pos < cur) continue;
if (pos > cur) vec.emplace_back(D(cur), pos - cur); // ->
vec.emplace_back(D(p), 1), cur = pos + 1; // 跨过 p -> p+1
}
vec.emplace_back(D(cur), _abs(offset)); // 整体
} else {
int cur = p;
vector<int> tmp = {p1 + 1, p2 + 1};
sort(tmp.begin(), tmp.end(), greater<int>());
for (int pos : tmp) {
if (pos > cur) continue;
if (pos < cur) vec.emplace_back(D(cur), cur - pos); // <-
vec.emplace_back(D(p), 1), cur = pos - 1; // 跨过 p-1 <- p
}
vec.emplace_back(D(cur), _abs(offset)); // 整体
}
}
};
work2();
sort(vec.begin(), vec.end());
int128 res = cost, need = _abs(offset);
for (auto [val, cnt] : vec) {
int128 w = min(cnt, need);
res += w * val, need -= w;
if (need <= 0) break;
} cout << static_cast<u64>(res / 2);
}也可以使用优先队列来维护调整法的过程。
:::::
6.8 循环铲雪
给定长度为 n n n 的序列 a a a,有 q q q 次询问。
一次询问给出 l , r , m l,r,m l,r,m,求解如下问题:每次操作将一个区间内的所有元素 ± 1 \pm 1 ±1 对 m m m 取模,求使所有元素变为 0 0 0 的最小操作次数。
n ≤ 2 × 10 5 n \le 2 \times 10^5 n≤2×105, q ≤ 10 5 q \le 10^5 q≤105,5 秒,250 MB。
:::::success[题解]
考虑 2.1 的差分法。
设 d i = a i − a i − 1 d_i=a_i-a_{i-1} di=ai−ai−1,特别地 d l = a l , d r + 1 = − a r d_l=a_l,d_{r+1}=-a_r dl=al,dr+1=−ar,于是:
- 原操作等价于:选择两个下标 l ≤ i < j ≤ r l \le i < j \le r l≤i<j≤r,令 d i ← d i ± 1 d_i \gets d_i \pm 1 di←di±1, d j ← d j ∓ 1 d_j \gets d_j \mp 1 dj←dj∓1。
- 目标状态为 ∀ l ≤ i ≤ r + 1 , d i ≡ 0 ( m o d m ) \forall l \le i \le r+1, d_i \equiv 0 \pmod m ∀l≤i≤r+1,di≡0(modm)。
注意到如果 ∣ d i ∣ ≥ 2 m |d_i| \ge 2m ∣di∣≥2m,直接调整不如先模 m m m 再处理,因此最优时 d i d_i di 只会落在 { − m , 0 , m } \{-m, 0, m\} {−m,0,m} 中,且 − m -m −m 与 m m m 必须成对出现。
如果忽略取模的限制,根据 2.1 结论,最小操作次数为 1 2 ∑ i = l r + 1 ∣ d i ∣ \dfrac{1}{2} \sum \limits_{i=l}^{r+1} |d_i| 21i=l∑r+1∣di∣,即每个 d i d_i di 贡献 ∣ d i ∣ |d_i| ∣di∣。
现在考虑模 m m m 的影响,相当于我们可以预先将某些 d i d_i di 加上或减去 m m m:
- 若 d i < 0 d_i < 0 di<0,可预先加上 m m m,此时对答案的额外贡献为 m + 2 d i m + 2d_i m+2di。
- 若 d i > 0 d_i > 0 di>0,可预先减去 m m m,此时对答案的额外贡献为 m − 2 d i m - 2d_i m−2di。
记这两种决策分别为 X X X 和 Y Y Y。由于 − m -m −m 和 m m m 必须成对出现,因此 X X X 和 Y Y Y 的数量也必须相等。将所有 X X X 决策的贡献值 x i x_i xi 和 Y Y Y 决策的贡献值 y i y_i yi 分别升序排序,并取其前缀和,则总答案为:
1 2 ( ∑ i = l r ∣ d i ∣ + min k ( ∑ i = 0 k x i + ∑ i = 0 k y i ) ) \dfrac{1}{2} \left(\sum {i=l}^r |d_i|+\min{k} \left(\sum_{i=0}^k x_i+\sum_{i=0}^k y_i\right)\right) 21(i=l∑r∣di∣+kmin(i=0∑kxi+i=0∑kyi))
因此我们得到一个 O ( n q log n ) O(nq \log n) O(nqlogn) 的做法:
cpp
int solve(int l, int r, int m) {
vector<int> x, y;
int sum = 0;
for (int i = l; i <= r + 1; i++) {
int d = a[i] - a[i - 1];
if (i == l) d = a[l];
if (i == r + 1) d = -a[r];
if (d < 0) x.emplace_back(m + 2 * d);
else y.emplace_back(m - 2 * d);
sum += abs(d);
}
sort(x.begin(), x.end()), sort(y.begin(), y.end());
int xn = x.size(), yn = y.size();
for (int i = 1; i < xn; i++) x[i] += x[i - 1];
for (int i = 1; i < yn; i++) y[i] += y[i - 1];
int res = sum;
for (int i = 0; i < min(xn, yn); i++) res = min(res, sum + x[i] + y[i]);
return res / 2;
}对着这段代码优化。
记 f ( k ) = ∑ i = 0 k x i + ∑ i = 0 k y i f(k)=\sum \limits_{i=0}^k x_i+\sum \limits_{i=0}^k y_i f(k)=i=0∑kxi+i=0∑kyi,将 f ( k ) f(k) f(k) 打表出来可以发现 f ( k ) f(k) f(k) 是单谷的,下面证明这一发现。
将所有正差分 d i d_i di 记为 p p p,所有负差分 d i d_i di 记为 q q q。
f ( k ) = ∑ i = 0 k x i + ∑ i = 0 k y i = ∑ i = 0 k ( 2 m + 2 ( p i − q i ) ) = 2 m k + 2 ∑ i = 0 k ( p i − q i ) Δ f ( k ) = 2 m + 2 ( p k + 1 − q k + 1 ) \begin{aligned} f(k)&=\sum \limits_{i=0}^k x_i+\sum \limits_{i=0}^k y_i\\ &=\sum \limits_{i=0}^k \left(2m+2(p_i-q_i)\right)\\ &=2mk+2\sum_{i=0}^k (p_i-q_i)\\ \Delta f(k) &=2m+2(p_{k+1}-q_{k+1}) \end{aligned} f(k)Δf(k)=i=0∑kxi+i=0∑kyi=i=0∑k(2m+2(pi−qi))=2mk+2i=0∑k(pi−qi)=2m+2(pk+1−qk+1)由 p i p_i pi 单调不降, q i q_i qi 单调不升, p i − q i p_i-q_i pi−qi 单调不降。则 Δ f ( k ) \Delta f(k) Δf(k) 单调不降,即 f ( k ) f(k) f(k) 有凸性。
得到这个结论以后,我们可以直接三分出谷点。瓶颈仅在于求 x , y x,y x,y。
注意到 x i x_i xi 和 y i y_i yi 可由 d i d_i di 直接计算,且 d i d_i di 随下标连续变化,我们可以用两棵可持久化权值线段树来维护所有 x i , y i x_i,y_i xi,yi 的值,并支持查询前 k k k 小的 x i , y i x_i,y_i xi,yi 之和。
具体实现时, d l d_l dl 和 d r + 1 d_{r+1} dr+1 需要单独处理,可以在线段树二分时带一个参数。为了方便编写,代码中的数字取了相反数。
复杂度 O ( q log n log V ) O(q \log n \log V) O(qlognlogV)。实现细节上,应当注意特判 l = r l=r l=r 和一些边界的处理。
cpp
const int N = 2e5 + 5, M = 1 << 30;
int n, q, l, r, m, a[N], cx[N], cy[N], pre[N];
struct segtree {
#define ls lson[rt]
#define rs rson[rt]
int tot, root[N], lson[N << 5], rson[N << 5], cnt[N << 5], sum[N << 5];
void pushup(int rt) {cnt[rt] = cnt[ls] + cnt[rs], sum[rt] = sum[ls] + sum[rs];}
int clone(int rt) {
int u = ++tot;
lson[u] = ls, rson[u] = rs, cnt[u] = cnt[rt], sum[u] = sum[rt];
return u;
}
int insert(int x, int l, int r, int rt) {
int p = clone(rt);
if (l == r) return cnt[p]++, sum[p] += l, p;
int mid = (l + r) >> 1;
if (x <= mid) lson[p] = insert(x, l, mid, ls);
else rson[p] = insert(x, mid + 1, r, rs);
return pushup(p), p;
}
int ask(int k, int x, int l, int r, int u, int v) {
if (k == 0) return 0;
if (l == r) return k * l;
int mid = (l + r) >> 1, num = cnt[rson[u]] - cnt[rson[v]] + (mid < x && x <= r);
if (num >= k) return ask(k, x, mid + 1, r, rson[u], rson[v]);
int val = sum[rson[u]] - sum[rson[v]] + (mid < x && x <= r ? x : 0);
return ask(k - num, x, l, mid, lson[u], lson[v]) + val;
}
segtree() : tot(0) {root[0] = 0, lson[0] = rson[0] = cnt[0] = sum[0] = 0;}
int ask(int l, int r, int k, int x) {return ask(k, x, 0, M, root[r], root[l - 1]);}
void push(int x) {root[x] = root[x - 1];}
void push(int x, int v) {root[x] = insert(v, 0, M, root[x - 1]);}
} X, Y;
void _main() {
cin >> n >> q;
for (int i = 1; i <= n; i++) cin >> a[i];
for (int i = 1; i <= n + 1; i++) {
int d = a[i] - a[i - 1];
pre[i] = pre[i - 1] + abs(d), cx[i] = cx[i - 1], cy[i] = cy[i - 1];
if (d < 0) X.push(i, -d), Y.push(i), cx[i]++;
else X.push(i), Y.push(i, d), cy[i]++;
}
while (q--) {
cin >> l >> r >> m;
if (l == r) {cout << min(a[l], m - a[l]) << '\n'; continue;}
int sum = pre[r] - pre[l] + a[l] + a[r];
auto f = [&](int k) -> int {return sum / 2 + m * k - X.ask(l + 1, r, k, a[r]) - Y.ask(l + 1, r, k, a[l]);};
auto sol = [&](int l, int r) -> int {
int p = 0;
while (l <= r) {
int m1 = l + (r - l) / 3, m2 = r - (r - l) / 3;
if (f(m1) < f(m2)) r = m2 - 1, p = m1;
else l = m1 + 1, p = m2;
} return p;
};
int p = sol(0, min(cx[r] - cx[l], cy[r] - cy[l]) + 1);
cout << min(sum / 2, f(p)) << '\n';
}
}:::::
6.9 循环铲雪·改
给出 q q q 次操作,每次操作对 a a a 中不小于 u u u 的数加上 v v v,然后查询以 m + v m+v m+v 为模数的链上循环铲雪。操作之间独立。
1 ≤ n , q ≤ 2 × 10 5 1 \le n, q \le 2\times 10^5 1≤n,q≤2×105,3 秒,512 MB。
:::::success[题解]
在 6.8 中,我们注意到 f ( k ) f(k) f(k) 是单谷函数,因此可以三分答案,这在本题中仍然适用。需要考虑如何动态维护 x , y x,y x,y。
对于一次询问 ( u , v ) (u, v) (u,v),考虑差分 d i = a i − a i − 1 d_i = a_i - a_{i-1} di=ai−ai−1 的变化情况:
- 若 a i ≥ u , a i − 1 ≥ u a_i \ge u, a_{i-1} \ge u ai≥u,ai−1≥u, d i d_i di 不变。
- 若 a i < u , a i − 1 < u a_i < u, a_{i-1} < u ai<u,ai−1<u, d i d_i di 不变。
- 若 a i ≥ u , a i − 1 < u a_i \ge u, a_{i-1} < u ai≥u,ai−1<u,此时原 d i > 0 d_i>0 di>0 且 d i ← d i + v d_i \gets d_i+v di←di+v。
- 若 a i < u , a i − 1 ≥ u a_i < u, a_{i-1} \ge u ai<u,ai−1≥u,此时原 d i < 0 d_i < 0 di<0 且 d i ← d i − v d_i \gets d_i-v di←di−v。
综上,当 u ∈ ( min ( a i , a i − 1 ) , max ( a i , a i − 1 ) ] u \in \left(\min(a_i, a_{i-1}), \max(a_i, a_{i-1})\right] u∈(min(ai,ai−1),max(ai,ai−1)] 时, ∣ d i ∣ ← ∣ d i ∣ + v |d_i|\gets |d_i|+v ∣di∣←∣di∣+v。
将询问离线并且按 u u u 升序排序,对 u u u 扫描线。随着 u u u 的增大,每个 d i d_i di 会在不变和加 v v v 之间切换。
我们可以用开四个数据结构,维护不变的正差分 P 0 P_0 P0,加 v v v 的正差分 P 1 P_1 P1,不变的负差分 N 0 N_0 N0,减 v v v 的负差分 N 1 N_1 N1。扫描线的过程中容易更新这四个集合。
需要查询 x x x 中前 k k k 大数的和。可以视为对 P 1 P_1 P1 打一个全局加标记 v v v 以后,查询 P 0 ∪ P 1 P_0 \cup P_1 P0∪P1 的前 k k k 大数之和。对于 y y y 同理。
可以使用 FHQ-Treap 维护 P 0 , P 1 , N 0 , N 1 P_0,P_1,N_0,N_1 P0,P1,N0,N1,支持插入删除和并集查询。由于外层需要三分,复杂度为 O ( q log 2 n ) O(q \log^2 n) O(qlog2n)。代码改成了二分。
cpp
int n, m, q, a[N], d[N], ans[N];
mt19937 rand32(chrono::steady_clock::now().time_since_epoch().count());
struct node {
node *ls, *rs;
int size, val, sum;
unsigned prio;
node() : ls(nullptr), rs(nullptr), size(1), val(0), sum(0), prio(rand32()) {}
node(int x) : ls(nullptr), rs(nullptr), size(1), val(x), sum(x), prio(rand32()) {}
node* pushup() {
size = 1, sum = val;
if (ls) size += ls->size, sum += ls->sum;
if (rs) size += rs->size, sum += rs->sum;
return this;
}
};
int S(node *u) {return u ? u->size : 0;}
void split(node* u, int val, node*& x, node*& y) {
if (!u) return x = y = nullptr, void();
if (u->val <= val) x = u, split(u->rs, val, u->rs, y);
else y = u, split(u->ls, val, x, u->ls);
u->pushup();
}
node* merge(node* a, node* b) {
if (!a || !b) return a ? a : b;
return (a->prio < b->prio)
? (a->rs = merge(a->rs, b), a->pushup())
: (b->ls = merge(a, b->ls), b->pushup());
}
void insert(node*& u, int val) {
node *x, *y; split(u, val, x, y);
u = merge(merge(x, new node(val)), y);
}
void remove(node*& u, int val) {
node *x, *y, *z;
split(u, val, x, z), split(x, val - 1, x, y);
if (y) y = merge(y->ls, y->rs);
u = merge(merge(x, y), z);
}
int kth(node* u, int k) {
while (u) {
if (k == S(u->rs) + 1) return u->val;
if (k <= S(u->rs)) u = u->rs;
else k -= S(u->rs) + 1, u = u->ls;
} return 0;
}
int sum(node* u, int k) {
int res = 0;
while (u && k > 0) {
if (k <= S(u->rs)) u = u->rs;
else res += (u->rs ? u->rs->sum : 0) + u->val, k -= S(u->rs) + 1, u = u->ls;
} return res;
}
int kth(node* u1, int v1, node* u2, int v2, int k) {
if (!u1) return kth(u2, k) + v2;
if (!u2) return kth(u1, k) + v1;
if (k <= 0) return 0;
int w1 = u1->val + v1, w2 = u2->val + v2;
if (w1 < w2) swap(u1, u2), swap(v1, v2);
int s1 = S(u1->rs), s2 = S(u2->rs);
return k <= s1 + s2 + 1 ? kth(u1, v1, u2->rs, v2, k) : kth(u1->ls, v1, u2, v2, k - s1 - 1);
}
int sum(node* u1, int v1, node* u2, int v2, int k) {
if (!u1) return sum(u2, k) + v2 * k;
if (!u2) return sum(u1, k) + v1 * k;
if (k <= 0) return 0;
int w1 = u1->val + v1, w2 = u2->val + v2;
if (w1 < w2) swap(u1, u2), swap(v1, v2);
int s1 = S(u1->rs), s2 = S(u2->rs);
if (k <= s1 + s2 + 1) return sum(u1, v1, u2->rs, v2, k);
int p = (u1->rs ? u1->rs->sum : 0) + u1->val + v1 * (s1 + 1);
return p + sum(u1->ls, v1, u2, v2, k - s1 - 1);
}
node *P0, *P1, *N0, *N1;
vector<tuple<int, int, int>> qry; // [u, v, id]
vector<tuple<int, int, int>> line; // [u, type, pos]
void prework() {
P0 = P1 = N0 = N1 = nullptr;
for (int i = 1; i <= n + 1; i++) {
d[i] = a[i] - a[i - 1];
int x = min(a[i], a[i - 1]), y = max(a[i], a[i - 1]);
if (x < y) line.emplace_back(x + 1, 1, i), line.emplace_back(y + 1, -1, i);
if (d[i] > 0) insert(P0, d[i]);
else insert(N0, -d[i]);
}
sort(line.begin(), line.end());
}
void update(int x) {
auto [u, type, pos] = line[x];
if (d[pos] > 0) {
if (type == 1) remove(P0, d[pos]), insert(P1, d[pos]);
else remove(P1, d[pos]), insert(P0, d[pos]);
} else {
if (type == 1) remove(N0, -d[pos]), insert(N1, -d[pos]);
else remove(N1, -d[pos]), insert(N0, -d[pos]);
}
}
void _main() {
cin >> n >> m >> q;
for (int i = 1; i <= n; i++) cin >> a[i];
for (int i = 1, u, v; i <= q; i++) {
cin >> v >> u;
qry.emplace_back(u, v, i);
}
sort(qry.begin(), qry.end());
prework();
int p = 0, lim = line.size();
for (const auto& [u, v, id] : qry) {
while (p < lim && get<0>(line[p]) <= u) update(p++);
int l = 0, r = min(S(P0) + S(P1), S(N0) + S(N1)), k = 0;
while (l <= r) {
int mid = (l + r) >> 1;
if (mid == 0) {l = 1; continue;}
int x = kth(P0, 0, P1, v, mid), y = kth(N0, 0, N1, v, mid);
if (x + y > m + v) k = mid, l = mid + 1;
else r = mid - 1;
}
int x = sum(P0, 0, P1, v, k), y = sum(N0, 0, N1, v, k);
int tot = (P0 ? P0->sum : 0) + (P1 ? P1->sum : 0) + S(P1) * v
+ (N0 ? N0->sum : 0) + (N1 ? N1->sum : 0) + S(N1) * v;
ans[id] = tot + 2 * k * (m + v) - 2 * (x + y);
}
for (int i = 1; i <= q; i++) cout << ans[i] / 2 << '\n';
}:::::
6.10 WC2025 T3
给出 n n n 个二元组 ( a i , b i ) (a_i,b_i) (ai,bi),一次操作支付 m m m 的代价,将一个区间上的所有 a i a_i ai 减 1 1 1。所有操作结束后,你的得分为 ∑ i = 1 n b i [ a i ≤ 0 ] \sum\limits_{i=1}^n b_i[a_i \le 0] i=1∑nbi[ai≤0]。
最大化得分减去代价的值。
多测, ∑ n ≤ 5 × 10 5 \sum n \le 5 \times 10^5 ∑n≤5×105, 1 ≤ a i , m ≤ 10 9 1 \le a_i,m \le 10^9 1≤ai,m≤109, − 10 9 ≤ b i ≤ 10 9 -10^9 \le b_i \le 10^9 −109≤bi≤109。2 秒,1024 MB。
:::::success[题解]
根据 2.1 给出的构造,我们任意赋一组非负整数 x i x_i xi 表示第 i i i 个位置被操作的次数,总能找到一种方案。这时的最小操作次数为 ∑ i = 1 n max ( 0 , x i − x i − 1 ) \sum \limits_{i=1}^n \max(0,x_i-x_{i-1}) i=1∑nmax(0,xi−xi−1)。
写出答案式子为
∑ i = 1 n b i [ x i ≥ a i ] − m ∑ i = 1 n max ( 0 , x i − x i − 1 ) = ∑ i = 1 n ( b i [ x i ≥ a i ] − m × max ( 0 , x i − x i − 1 ) ) \sum {i=1}^n b_i[x_i \ge a_i]-m\sum {i=1}^n \max(0,x_i-x{i-1})\\ =\sum{i=1}^n \left(b_i[x_i \ge a_i]-m \times \max(0,x_i-x_{i-1})\right) i=1∑nbi[xi≥ai]−mi=1∑nmax(0,xi−xi−1)=i=1∑n(bi[xi≥ai]−m×max(0,xi−xi−1))
容易把贡献拆到每个位置 i i i 上。据此设计一个 DP,令 f i , j f_{i,j} fi,j 表示考虑前 i i i 个元素,满足 x i = j x_i=j xi=j 时前缀的最大得分,转移是平凡的,做到 O ( n V ) O(nV) O(nV)。这个东西很难优化,所以需要先把状态压下来。
进一步,考察操作的性质。注意到令 x i ← x i − 1 x_i \gets x_{i-1} xi←xi−1 总能避免 m m m 的代价。考虑 x i x_i xi 序列的形态,则其仅在特定位置产生突变。具体地:
- 当 b i > 0 b_i>0 bi>0 时,有决策 x i ← a i x_i \gets a_i xi←ai,获得 b i b_i bi 的得分。
- 当 b i < 0 b_i<0 bi<0 时,有决策 x i ← a i − 1 x_i \gets a_i-1 xi←ai−1,避免 − b i -b_i −bi 的代价。
此时我们并不需要记录 O ( V ) O(V) O(V) 种决策,直接将状态改为: f i f_i fi 表示考虑前 i i i 个元素,且 i i i 处产生突变的最大得分。我们记 c i = a i − [ b i < 0 ] c_i=a_i-[b_i<0] ci=ai−[bi<0],则 f i f_i fi 是原本的 f i , c i f_{i,c_i} fi,ci。
枚举上一个突变点 j j j,此时 ∀ k ∈ [ j , i ) , x i ← c j \forall k \in [j,i), x_i \gets c_j ∀k∈[j,i),xi←cj。二者之间产生 m × max ( 0 , c i − c j ) m \times \max(0,c_i-c_j) m×max(0,ci−cj) 的代价。同时我们需要枚举 k ∈ ( j , i ) k \in (j,i) k∈(j,i) 判断这些点是否被顺带消除,得到式子:
f i = max ( 0 , b i ) + max j = 0 i − 1 ( f j − m × max ( 0 , c i − c j ) + ∑ k = j + 1 i − 1 b k [ c i ≥ a k ] ) f_i=\max(0,b_i)+\max_{j=0}^{i-1} \left(f_j - m \times \max(0,c_i-c_j) +\sum_{k=j+1}^{i-1} b_k [c_i \ge a_k] \right) fi=max(0,bi)+j=0maxi−1 fj−m×max(0,ci−cj)+k=j+1∑i−1bk[ci≥ak]
倒序枚举 j j j 即可动态维护后面那个求和式,做到 O ( n 2 ) O(n^2) O(n2),获得 35pts。
cpp
int n, m, a[N], b[N], c[N], f[N];
void _main() {
cin >> n >> m;
for (int i = 1; i <= n; i++) cin >> a[i] >> b[i], c[i] = a[i] - (b[i] < 0);
fill(f + 1, f + n + 1, -1e18);
for (int i = 1; i <= n; i++) {
int v = 0;
for (int j = i - 1; j >= 0; j--) {
f[i] = max(f[i], max(0LL, b[i]) + f[j] - m * max(0LL, c[i] - c[j]) + v);
if (c[i] >= a[j]) v += b[j];
}
}
cout << *max_element(f, f + n + 1) << '\n';
}令 h ( l , r ) = ∑ k = l + 1 r − 1 b k [ c r ≥ a k ] h(l,r)=\sum\limits_{k=l+1}^{r-1} b_k [c_r \ge a_k] h(l,r)=k=l+1∑r−1bk[cr≥ak]。注意到转移式中有 max ( 0 , c i − c j ) \max(0,c_i-c_j) max(0,ci−cj) 这个东西,考虑分类讨论:
- 若 c j ≥ c i c_j \ge c_i cj≥ci,此时无消除代价,我们需要查询 c j ∈ [ c i , + ∞ ) c_j \in [c_i,+\infty) cj∈[ci,+∞) 的最大得分 f j + h ( j , i ) f_j+h(j,i) fj+h(j,i)。
- 若 c j < c i c_j < c_i cj<ci,此时支付 m ( c i − c j ) m(c_i-c_j) m(ci−cj) 的代价,我们需要查询 c j ∈ [ 0 , c i ] c_j \in [0,c_i] cj∈[0,ci] 的最大得分 f j + m × c j + h ( j , i ) f_j+m\times c_j+h(j,i) fj+m×cj+h(j,i)。
离散化以后,将两棵线段树建在 c i c_i ci 上,分别维护两种情况,需要支持区间加、区间 chkmax,复杂度 O ( n log n ) O(n \log n) O(nlogn)。
cpp
int n, m, len, a[N], b[N], c[N], d[N << 1];
int idx(int x) {return lower_bound(d + 1, d + len + 1, x) - d;}
struct segtree {
#define ls (rt << 1)
#define rs (rt << 1 | 1)
constexpr static int inf = 1e18;
int val[N << 3], add[N << 3], cmax[N << 3];
void pushup(int rt) {val[rt] = max(val[ls], val[rs]);}
void apply(int rt, int ad, int cm) {
val[rt] = max(val[rt] + ad, cm), add[rt] += ad;
cmax[rt] = max(cmax[rt] + ad, cm);
}
void pushdown(int rt) {
apply(ls, add[rt], cmax[rt]), apply(rs, add[rt], cmax[rt]), add[rt] = 0, cmax[rt] = -inf;
}
void build(int l = 0, int r = len, int rt = 1) {
add[rt] = 0, cmax[rt] = -inf, val[rt] = -inf;
if (l == r) return;
int mid = (l + r) >> 1;
build(l, mid, ls), build(mid + 1, r, rs);
}
void uadd(int tl, int tr, int c, int l = 0, int r = len, int rt = 1) {
if (tl <= l && r <= tr) return apply(rt, c, -inf), void();
int mid = (l + r) >> 1;
pushdown(rt);
if (tl <= mid) uadd(tl, tr, c, l, mid, ls);
if (tr > mid) uadd(tl, tr, c, mid + 1, r, rs);
pushup(rt);
}
void umax(int tl, int tr, int c, int l = 0, int r = len, int rt = 1) {
if (tl <= l && r <= tr) return apply(rt, 0, c), void();
int mid = (l + r) >> 1;
pushdown(rt);
if (tl <= mid) umax(tl, tr, c, l, mid, ls);
if (tr > mid) umax(tl, tr, c, mid + 1, r, rs);
pushup(rt);
}
int ask(int x, int l = 0, int r = len, int rt = 1) {
if (l == r) return val[rt];
int mid = (l + r) >> 1;
pushdown(rt);
return x <= mid ? ask(x, l, mid, ls) : ask(x, mid + 1, r, rs);
}
} T1, T2;
void _main() {
cin >> n >> m, len = 0;
for (int i = 1; i <= n; i++) {
cin >> a[i] >> b[i], c[i] = a[i] - (b[i] < 0);
d[++len] = a[i], d[++len] = a[i] - 1;
}
sort(d + 1, d + len + 1), len = unique(d + 1, d + len + 1) - d - 1;
T1.build(), T2.build();
T1.umax(0, 0, 0), T2.umax(0, len, 0);
for (int i = 1; i <= n; i++) {
int v1 = T1.ask(idx(c[i])), v2 = T2.ask(idx(c[i])) - m * c[i];
int v = max(v1, v2) + max(0LL, b[i]);
T1.uadd(idx(a[i]), len, b[i]), T2.uadd(idx(a[i]), len, b[i]);
T1.umax(0, idx(c[i]), v), T2.umax(idx(c[i]), len, v + m * c[i]);
} cout << T1.val[1] << '\n';
}:::::
6.11 一道模拟赛题
某场模拟赛的题目。
给出一棵树,每个点有点权 a i a_i ai,每条边有边权。一次操作花费 a u + a v a_u+a_v au+av 的代价,将从 u u u 到 v v v 的简单路径上所有边权减 1 1 1。要求操作过程中边权非负。
给出 q q q 次修改,每次修改给出 ( u , v , w ) (u,v,w) (u,v,w),将从 u u u 到 v v v 的简单路径上所有边权加上 w w w。在每次修改结束后,求出使得所有边权变为 0 0 0 的最小操作次数。
n , q × 2 × 10 5 n, q \times 2 \times 10^5 n,q×2×105。3 秒,512 MB。
:::::success[题解]
考虑 4.1 的插头法。对于点 u u u,我们记
S u = ∑ ( u , v , w ) ∈ E w M u = max ( u , v , w ) ∈ E w S_u=\sum \limits_{(u,v,w) \in E} w\\ M_u=\max \limits_{(u,v,w) \in E} w Su=(u,v,w)∈E∑wMu=(u,v,w)∈Emaxw
对于延伸到 u u u 的插头,我们希望插头尽量合并。注意到有过多插头来自同一个 v v v 时,同一来源的插头可能无法全部配对。
- 当 2 M u > S u 2M_u>S_u 2Mu>Su 时,我们必须新建 2 M u − S u 2M_u-S_u 2Mu−Su 个插头。这也是 6.4 得到的结论。
- 当 2 M u ≤ S u 2M_u \le S_u 2Mu≤Su 时,则我们可以完成 ⌊ S u 2 ⌋ \left\lfloor \dfrac{S_u}{2} \right\rfloor ⌊2Su⌋ 次插头配对。此时新建 S u m o d 2 S_u \bmod 2 Sumod2 个插头。
将贡献乘上点权即可得到答案:
cpp
int solve() {
int res = 0;
for (int u = 1; u <= n; u++) {
int sum = 0, mx = 0;
for (auto [v, w] : e[u]) sum += w, mx = max(mx, w);
if (2 * mx > sum) res += (2 * mx - sum) * a[u];
else if (sum & 1) res += a[u];
} return res;
}进一步,考虑用数据结构维护上述过程。将树重链剖分后,我们将点分为三类:
- A 类点:满足 2 M u > S u 2M_u>S_u 2Mu>Su 且 M u M_u Mu 位于重链上;
- B 类点:满足 2 M u > S u 2M_u>S_u 2Mu>Su 且 M u M_u Mu 位于轻儿子中;
- C 类点:满足 2 M u ≤ S u 2M_u \le S_u 2Mu≤Su。
对于一次修改,除去路径端点以后其余点都有两条邻边被修改。
- 对于 A 类点,我们发现其贡献是 2 ( M u + w ) − ( S u + 2 w ) = 2 M u − S u 2(M_u+w)-(S_u+2w)=2M_u-S_u 2(Mu+w)−(Su+2w)=2Mu−Su,不变。
- 对于 B 类点,其贡献变为 2 M u − ( S u + 2 w ) = 2 M u − S u − 2 w 2M_u-(S_u+2w)=2M_u-S_u-2w 2Mu−(Su+2w)=2Mu−Su−2w。若贡献为负,则其变为一个 C 类点。
- 对于 C 类点,若 S u ← S u + 2 w S_u \gets S_u + 2w Su←Su+2w, M u M_u Mu 最多变为 M u + w M_u+w Mu+w,故其仍然满足 2 M u ≤ S u 2M_u \le S_u 2Mu≤Su。且 S u m o d 2 S_u \bmod 2 Sumod2 不改变,其贡献不变。
因此,只需维护 B 类点的贡献。
我们建立一棵线段树维护如下信息:
- 重儿子、父亲、轻儿子的边权;
- 当前节点的点权和 S u S_u Su;
- B 类点的贡献和;
- 当前节点内是否存在 B 类点,B 类点贡献的最小值;
- 当前节点的答案。
其余的一些信息可以合并,使用懒标记维护。另一些信息则需要重构处理。
在每次修改结束后,重构整棵线段树,若子树不存在 B 类点或 B 类点贡献最小值为正,结束递归。
可以势能分析说明该策略是 O ( q log 2 n ) O(q \log^2 n) O(qlog2n) 的。
cpp
#define int long long
const int N = 2e5 + 5, inf = 1e18;
int n, q, a[N];
vector<pair<int, int>> e[N];
int dn, fa[N], dep[N], sz[N], son[N], top[N], dfn[N], rev[N], ef[N], light[N], sum[N];
void dfs1(int u) {
sz[u] = 1;
for (auto [v, w] : e[u]) {
sum[u] += w;
if (v == fa[u]) continue;
dep[v] = dep[u] + 1, fa[v] = u, ef[v] = w, dfs1(v), sz[u] += sz[v];
if (sz[v] > sz[son[u]]) son[u] = v;
}
}
void dfs2(int u, int t) {
top[u] = t, dfn[u] = ++dn, rev[dn] = u;
if (son[u]) dfs2(son[u], t);
for (auto [v, w] : e[u]) {
if (v != fa[u] && v != son[u]) dfs2(v, v), light[u] = max(light[u], w);
}
}
struct node {
int son, fa, light; // 重儿子边权、返祖边边权、轻儿子边权最大值
int w; // 点权
int sum; // S_u
int val; // 答案
int sumb; // B 类点贡献和
int mn; // B 类点贡献最小值
bool B; // 是否存在 B 类点
void rebuild() { // 重构
int m = max({son, fa, light});
if (2 * m <= sum) return B = false, val = (sum & 1) * w, sumb = 0, mn = inf, void();
val = (2 * m - sum) * w;
if (m > son && m > fa) B = true, sumb = w, mn = 2 * m - sum;
else B = false, sumb = 0, mn = inf;
}
};
node make(int u) {
node x;
x.fa = ef[u], x.son = ef[son[u]], x.light = light[u];
x.w = a[u], x.sum = sum[u];
return x.rebuild(), x;
}
struct segtree {
#define ls (rt << 1)
#define rs (rt << 1 | 1)
node val[N << 2];
int tag[N << 2];
void pushup(int rt) {
val[rt].sumb = val[ls].sumb + val[rs].sumb, val[rt].val = val[ls].val + val[rs].val;
val[rt].B = val[ls].B | val[rs].B, val[rt].mn = min(val[ls].mn, val[rs].mn);
}
void apply(int rt, int x) {
tag[rt] += x;
if (val[rt].B) val[rt].val -= 2 * x * val[rt].sumb, val[rt].mn -= 2 * x;
val[rt].sum += 2 * x, val[rt].son += x, val[rt].fa += x;
}
void pushdown(int rt) {
if (!tag[rt]) return;
apply(ls, tag[rt]), apply(rs, tag[rt]), tag[rt] = 0;
}
void add(int tl, int tr, int c, int l = 1, int r = n, int rt = 1) {
if (tl <= l && r <= tr) return apply(rt, c), void();
int mid = (l + r) >> 1;
pushdown(rt);
if (tl <= mid) add(tl, tr, c, l, mid, ls);
if (tr > mid) add(tl, tr, c, mid + 1, r, rs);
pushup(rt);
}
void maintain(int l = 1, int r = n, int rt = 1) {
if (!val[rt].B || val[rt].mn >= 0) return;
if (l == r) return val[rt].rebuild();
int mid = (l + r) >> 1;
pushdown(rt), maintain(l, mid, ls), maintain(mid + 1, r, rs), pushup(rt);
}
void ason(int x, int c, int l = 1, int r = n, int rt = 1) {
if (l == r) return val[rt].son += c, val[rt].sum += c, val[rt].rebuild();
int mid = (l + r) >> 1;
pushdown(rt);
if (x <= mid) ason(x, c, l, mid, ls);
else ason(x, c, mid + 1, r, rs);
pushup(rt);
}
void afa(int x, int c, int l = 1, int r = n, int rt = 1) {
if (l == r) return val[rt].fa += c, val[rt].sum += c, val[rt].rebuild();
int mid = (l + r) >> 1;
pushdown(rt);
if (x <= mid) afa(x, c, l, mid, ls);
else afa(x, c, mid + 1, r, rs);
pushup(rt);
}
void ulight(int x, int d, int v, int l = 1, int r = n, int rt = 1) {
if (l == r) return val[rt].light = max(val[rt].light, v), val[rt].sum += d, void();
int mid = (l + r) >> 1;
pushdown(rt);
if (x <= mid) ulight(x, d, v, l, mid, ls);
else ulight(x, d, v, mid + 1, r, rs);
pushup(rt);
}
node ask(int x, int l = 1, int r = n, int rt = 1) {
if (l == r) return val[rt];
int mid = (l + r) >> 1;
pushdown(rt);
return x <= mid ? ask(x, l, mid, ls) : ask(x, mid + 1, r, rs);
}
int all() {return val[1].val;}
void build(int l = 1, int r = n, int rt = 1) {
if (l == r) return val[rt] = make(rev[l]), void();
int mid = (l + r) >> 1;
build(l, mid, ls), build(mid + 1, r, rs), pushup(rt), val[rt].w = val[ls].w + val[rs].w;
}
} sgt;
void change(int u, int v, int c) {
while (top[u] != top[v]) {
if (dep[top[u]] < dep[top[v]]) swap(u, v);
if (u != top[u]) sgt.add(dfn[top[u]], dfn[u] - 1, c);
sgt.afa(dfn[u], c);
int v = sgt.ask(dfn[top[u]]).fa;
u = fa[top[u]];
sgt.ulight(dfn[u], c, v);
}
if (dep[u] < dep[v]) swap(u, v);
if (u == v) sgt.ason(dfn[u], 0);
else sgt.add(dfn[son[v]], dfn[fa[u]], c), sgt.afa(dfn[u], c), sgt.ason(dfn[v], c);
sgt.maintain();
}
void _main() {
cin >> n >> q;
for (int i = 1; i <= n; i++) cin >> a[i];
for (int i = 1, u, v, w; i < n; i++) {
cin >> u >> v >> w;
e[u].emplace_back(v, w), e[v].emplace_back(u, w);
}
dfs1(1), dfs2(1, 1), sgt.build();
cout << sgt.all() << '\n';
for (int u, v, w; q--; ) {
cin >> u >> v >> w;
change(u, v, w), cout << sgt.all() << '\n';
}
}:::::
6.12 CF1884E
给定长为 n n n 的序列 a i a_i ai,一次操作花费 ( r − l + 1 ) 2 (r-l+1)^2 (r−l+1)2 的代价,将 [ l , r ] [l,r] [l,r] 中的数字减去 1 1 1。
对 a a a 的所有循环位移求出:使所有数字都相等的最小操作次数。在此基础上,求出最小代价。
多测, ∑ n ≤ 10 6 \sum n \le 10^6 ∑n≤106,3 秒,250 MB。
:::::success[题解]
不难发现所有数字都变成最大值时,操作次数最小。
设最大值为 M M M,令 a i ← M − a i a_i \gets M-a_i ai←M−ai,问题就转化为序列铲雪。由 2.1 的结论得到第一问答案
∑ i = 1 n max ( 0 , a i − a i − 1 ) \sum_{i=1}^n \max(0,a_i-a_{i-1}) i=1∑nmax(0,ai−ai−1)
该值可以在循环位移过程中方便地维护。
对于第二问,我们则使用 2.2 的插头法。假设已处理完左侧,当前位于位置 i i i,左侧传来的右插头数量为 k k k,作如下讨论:
- 若 k ≥ a i k \ge a_i k≥ai:所有插头均可在此处被使用。每个插头贡献的长度为 i − p x + 1 i-p_x+1 i−px+1,因此代价为
∑ x = 1 k ( i − p x + 1 ) 2 = k ( i + 1 ) 2 + ∑ x = 1 k p x 2 − 2 ( i + 1 ) ∑ x = 1 k p x \sum_{x=1}^k (i-p_x+1)^2=k(i+1)^2+\sum_{x=1}^k {p_x}^2-2(i+1)\sum_{x=1}^k p_x x=1∑k(i−px+1)2=k(i+1)2+x=1∑kpx2−2(i+1)x=1∑kpx
处理完毕后, k ← k − a i k \gets k-a_i k←k−ai,且剩余插头的起点均变为 i i i。
-
若 k < a i k < a_i k<ai:此时需要额外创建 a i − k a_i-k ai−k 个插头,这些插头的起点就是 i i i。我们还需决定 k k k 个已有插头中哪些与当前的 a i a_i ai 配对。
根据直觉,越靠前的插头优先配对,得到的代价越小。
考虑证明这一观察。不妨考虑二元情况,即两个插头配对两个点的情况。
设两个插头的起点为 a , b a,b a,b,当前处理位置为 c c c,之后存在另一配对点 d d d。则 a < b < c < d a<b<c<d a<b<c<d。要证 ( b − c ) 2 + ( a − d ) 2 > ( a − c ) 2 + ( b − d ) 2 (b-c)^2+(a-d)^2>(a-c)^2+(b-d)^2 (b−c)2+(a−d)2>(a−c)2+(b−d)2,即证
( b − c ) 2 + ( a − d ) 2 − ( a − c ) 2 − ( b − d ) 2 > 0 b c + a d − a c − b d > 0 a ( d − c ) + b ( c − d ) > 0 ( b − a ) ( d − c ) > 0 \begin{aligned} (b-c)^2+(a-d)^2-(a-c)^2-(b-d)^2 &> 0\\ bc+ad-ac-bd &> 0\\ a(d-c)+b(c-d) &> 0\\ (b-a)(d-c) &> 0\\ \end{aligned} (b−c)2+(a−d)2−(a−c)2−(b−d)2bc+ad−ac−bda(d−c)+b(c−d)(b−a)(d−c)>0>0>0>0
上式显然成立。
因此,应将最靠前的 a i a_i ai 个插头在此处用完,其代价为
∑ x = 1 a i ( i − p x + 1 ) 2 = a i ( i + 1 ) 2 + ∑ x = 1 a i p x 2 − 2 ( i + 1 ) ∑ x = 1 a i p x \sum_{x=1}^{a_i} (i-p_x+1)^2=a_i(i+1)^2+\sum_{x=1}^{a_i} {p_x}^2-2(i+1) \sum_{x=1}^{a_i} p_x x=1∑ai(i−px+1)2=ai(i+1)2+x=1∑aipx2−2(i+1)x=1∑aipx
处理完毕后, k ← k − a i k \gets k - a_i k←k−ai,并删除 p p p 中的前 a i a_i ai 个起点。
综上所述,我们需要一种数据结构维护插头起点集合 p p p,支持前缀删除、前缀和以及前缀平方和查询。使用平衡树即可 O ( n log n ) O(n\log n) O(nlogn) 算出序列每个前缀的最小代价。
进一步,由于转化后 a a a 中至少有一个 0 0 0,我们选择任意一个 0 0 0 作为起点将环断开成链。因为没有任何操作会跨过这个断点,因此链上计算的代价就是整个环的代价。
从断点向左和向右做两次扫描,处理出序列的前缀代价和后缀代价。将结果合并,即可得到完整答案。
cpp
#define int long long
const int N = 1e6 + 5;
mt19937 rand32(chrono::steady_clock::now().time_since_epoch().count());
struct node {
unsigned prio;
node *ls, *rs;
int start, cnt, sum;
mint x, x2;
node(int a = 0, int b = 0)
: prio(rand32()), ls(nullptr), rs(nullptr), start(a),
cnt(b), sum(b), x((mint)a * b), x2((mint)a * a * b) {}
node* pushup() {
sum = cnt, x = (mint)start * cnt, x2 = (mint)start * start * cnt;
if (ls) sum += ls->sum, x += ls->x, x2 += ls->x2;
if (rs) sum += rs->sum, x += rs->x, x2 += rs->x2;
return this;
}
mint calc(mint pos) {return pos * pos * sum - x * pos * 2 + x2;}
};
node* merge(node* u, node* v) {
if (!u || !v) return u ? u : v;
return (u->prio < v->prio) ?
(u->rs = merge(u->rs, v), u->pushup()) :
(v->ls = merge(u, v->ls), v->pushup());
}
void split(node* u, int k, node*& x, node*& y) {
if (!u) return x = y = nullptr, void();
int ls = u->ls ? u->ls->sum : 0;
if (k <= ls) {
y = u, split(u->ls, k, x, u->ls), u->pushup();
} else if (k < ls + u->cnt) {
y = new node(u->start, u->cnt - k + ls), y->rs = u->rs, y->pushup();
u->cnt = k - ls, x = u, u->rs = nullptr, u->pushup();
} else {
x = u, split(u->rs, k - ls - u->cnt, u->rs, y), u->pushup();
}
}
int n, a[N];
pair<int, mint> pre[N], suf[N];
void solve(int n, pair<int, mint>* ans) {
node *rt = nullptr;
int cnt = 0; mint cost = 0;
for (int i = 1; i < n; i++) {
cnt += max(0LL, a[i] - a[i - 1]);
int ln = rt ? rt->sum : 0;
if (a[i] > ln) {
rt = merge(rt, new node(i, a[i] - ln));
} else if (a[i] < ln) {
node *x, *y; split(rt, a[i], x, y);
cost += y ? y->calc(i) : 0, rt = x;
}
ans[i] = {cnt, cost + (rt ? rt->calc(i + 1) : 0)};
}
}
void _main() {
cin >> n;
for (int i = 0; i < n; i++) cin >> a[i];
if (n == 1) return cout << "0 0\n", void();
int rot = max_element(a, a + n) - a, m = a[rot];
rotate(a, a + rot, a + n);
for (int i = 0; i < n; i++) a[i] = m - a[i];
solve(n, pre);
reverse(a + 1, a + n), solve(n, suf), reverse(suf + 1, suf + n);
for (int i = 0; i < n; i++) {
int k = (i - rot + n) % n, cnt = 0; mint cost = 0;
if (k > 0) cnt += suf[k].first, cost += suf[k].second;
if (k > 1) cnt += pre[k - 1].first, cost += pre[k - 1].second;
if (k == 0) cnt += pre[n - 1].first, cost += pre[n - 1].second;
cout << cnt << ' ' << cost << '\n';
}
} :::::
参考资料
- 1.3 线性规划基础------OI Wiki。
- 3.2 [ARC136C] Circular Addition 题解------braveTester。
- 4.1 P7246 手势密码------Alex_Wei。
- 6.4 题解 AT2304 【[AGC010C] Cleaning】------zhylj。