探索机器人运动规划的奇妙世界：从路径插值到轨迹再现

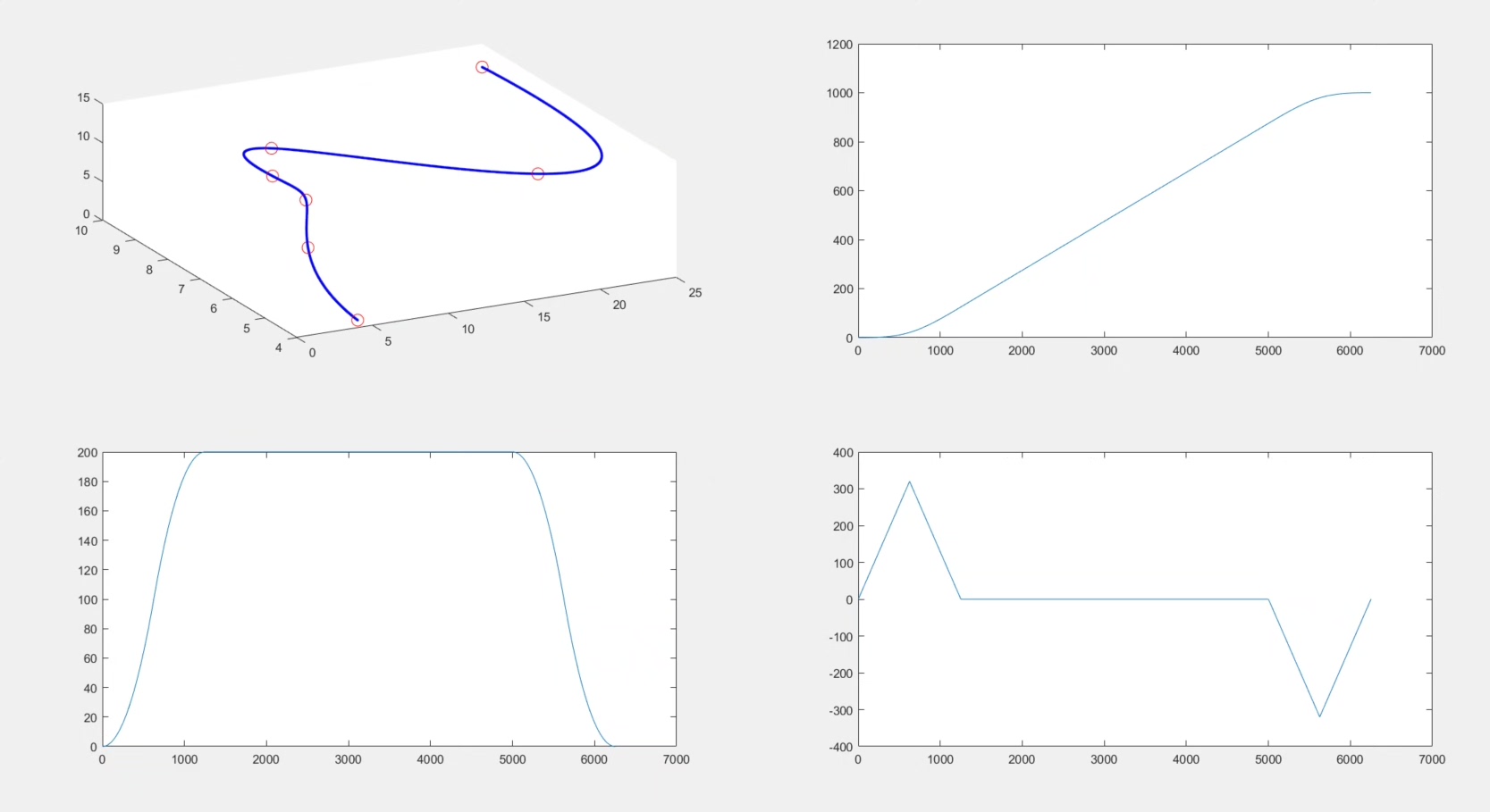
机器人空间任意点位路径插值 s型速度曲线轨迹规划实现机械臂指定非规则路径运动拖动示教的轨迹再现

在机器人的世界里，精准的运动控制就如同人类的灵动舞步，每一个动作都需要精心编排。今天咱们就来唠唠机器人空间任意点位路径插值、S 型速度曲线轨迹规划、实现机械臂指定非规则路径运动以及拖动示教的轨迹再现这些超有趣的话题。

机器人空间任意点位路径插值

想象一下，机器人要在空间中从 A 点移动到 B 点，可不是简单的直线过去就行，可能要绕过各种障碍物，这时候就需要路径插值啦。路径插值就是在给定的起始点和终点之间，按照一定的规则生成一系列中间点，让机器人的运动更加平滑合理。

咱们以二维平面为例，假设起始点为 start = (x1, y1)，终点为 end = (x2, y2)，通过线性插值的方法可以这样写代码：

python 复制代码

def linear_interpolation(start, end, num_points):
    x1, y1 = start
    x2, y2 = end
    points = []
    for i in range(num_points):
        t = i / (num_points - 1)
        x = x1 + t * (x2 - x1)
        y = y1 + t * (y2 - y1)
        points.append((x, y))
    return points

这段代码里，num_points 表示要生成的中间点数量。通过 t 这个参数从 0 变化到 1，计算出每个中间点的 x 和 y 坐标。这样机器人就能沿着这些点规划出一条相对平滑的路径啦。当然实际应用中可能会涉及到三维空间甚至更高维度，原理类似，只是坐标会更多。

S 型速度曲线轨迹规划

机器人运动的时候，如果突然加速或者减速，就像汽车猛地一脚油门一脚刹车，不仅不平稳，还可能对机械结构造成损伤。S 型速度曲线轨迹规划就像给机器人运动加了个"温柔滤镜"。

简单来说，S 型速度曲线在启动和停止阶段有一个加速度逐渐变化的过程，而不是瞬间加速到目标速度。下面是一个简化的 S 型速度曲线规划的思路代码（这里只简单模拟速度变化，不涉及实际运动控制部分）：

python 复制代码

import numpy as np
import matplotlib.pyplot as plt

def s_curve_velocity_profile(total_time, max_velocity, acceleration):
    # 加速阶段时间
    t1 = max_velocity / acceleration
    # 匀速阶段时间
    t2 = total_time - 2 * t1
    t = np.linspace(0, total_time, 1000)
    velocity = np.zeros_like(t)
    for i in range(len(t)):
        if t[i] < t1:
            velocity[i] = acceleration * t[i]
        elif t[i] < t1 + t2:
            velocity[i] = max_velocity
        else:
            velocity[i] = max_velocity - acceleration * (t[i] - t1 - t2)
    return t, velocity


total_time = 5
max_velocity = 10
acceleration = 5
t, v = s_curve_velocity_profile(total_time, max_velocity, acceleration)
plt.plot(t, v)
plt.xlabel('Time (s)')
plt.ylabel('Velocity')
plt.title('S - curve velocity profile')
plt.show()

在这段代码里，我们先计算出加速、匀速和减速阶段的时间，然后根据时间 t 的不同范围来计算对应的速度 velocity。最后用 matplotlib 把速度曲线画出来，你可以直观看到速度是如何平滑变化的。在实际的机器人运动控制中，结合这个速度曲线去控制机器人各关节的运动，就能让机器人的动作更加流畅和稳定。

实现机械臂指定非规则路径运动

机械臂要完成一些复杂的任务，比如在一堆杂乱的零件中抓取特定的一个，就需要沿着指定的非规则路径运动。这时候前面说的路径插值和速度曲线规划就要派上用场啦。

机器人空间任意点位路径插值 s型速度曲线轨迹规划实现机械臂指定非规则路径运动拖动示教的轨迹再现

假设我们已经通过某种方式获取到了非规则路径上的一系列点（可以是通过视觉识别得到物体位置，进而规划出的机械臂抓取路径点），我们可以先对这些点进行路径插值，然后再结合 S 型速度曲线来控制机械臂的运动。

python 复制代码

# 假设已经获取到非规则路径上的点
path_points = [(1, 1), (3, 5), (7, 4), (9, 2)]
num_interpolation_points = 50
interpolated_points = linear_interpolation(path_points[0], path_points[-1], num_interpolation_points)

# 假设运动总时间和最大速度等参数
total_motion_time = 10
max_arm_velocity = 8
acceleration = 4
t, v = s_curve_velocity_profile(total_motion_time, max_arm_velocity, acceleration)

# 这里只是简单示意如何结合两者，实际要根据机械臂运动学模型来控制各关节
# 比如根据速度曲线调整相邻点之间的运动时间
for i in range(len(interpolated_points) - 1):
    # 这里可以根据速度曲线 v 来计算从 interpolated_points[i] 到 interpolated_points[i + 1] 的运动时间
    # 实际代码要复杂得多，涉及到机械臂的逆运动学等
    pass

这里代码只是一个简单的框架，实际实现中要根据机械臂的具体运动学模型，通过逆运动学计算出每个关节的角度，再结合速度曲线控制关节的运动，从而实现沿着非规则路径的精确运动。

拖动示教的轨迹再现

拖动示教就像是手把手教机器人做事。你直接抓住机械臂，按照你想要的动作顺序拖动，机器人会记录下这个过程中的位置、姿态等信息。然后当需要再现这个轨迹的时候，机器人就按照记录的信息重复运动。

在记录部分，机器人要实时获取各个关节的角度或者末端执行器的位置和姿态等数据。假设我们用一个简单的列表来记录位置信息（实际可能更复杂，涉及到姿态等多方面数据）：

python 复制代码

recorded_positions = []
# 假设这里有个函数可以实时获取当前位置
def get_current_position():
    # 这里简单模拟返回一个位置坐标
    return (1, 2)

# 模拟拖动示教过程中记录位置
while is_dragging:
    position = get_current_position()
    recorded_positions.append(position)

在再现部分，机器人就按照记录的位置顺序，结合前面提到的路径插值和速度曲线规划来重现轨迹：

python 复制代码

for position in recorded_positions:
    # 这里结合路径插值和速度曲线规划，控制机械臂移动到 position
    # 同样实际要结合机械臂运动学模型
    pass

实际应用中，要考虑到记录数据的精度、噪声处理以及不同环境下的适应性等问题。但总体思路就是这样，通过拖动示教让机器人快速学习复杂的运动轨迹，然后精确再现。

机器人运动规划这一块充满了挑战与乐趣，从简单的路径插值到复杂的轨迹再现，每一步都在让机器人变得更加智能和灵活，期待未来能看到机器人在更多领域展现出令人惊叹的运动表现！