开篇介绍：
hello 大家！nice to 见到每一位屏幕前热爱编程、乐于钻研的小伙伴～ 不知道大家在学完 C++ 中 stack 和 queue 这两个经典容器后，是不是已经对 "先进后出""先进先出" 的特性了如指掌，对它们的接口用法也能熟练运用了呢？
在前面的博客里，我们从底层逻辑出发，一步步拆解了 stack 和 queue 的实现原理 ------ 无论是 stack 基于数组或链表的底层适配，还是 queue 为了满足首尾高效操作而选择的双向链表结构，亦或是它们作为 "适配器" 容器的设计思想，相信大家都已经在代码实践中慢慢消化吸收。
而学习容器的最终目的，从来都不只是 "会用"，更在于 "活用"------ 用容器的特性解决实际问题，让数据结构成为我们破解算法难题的 "利器"。所以呀，老规矩！今天咱们就趁热打铁，来上几道stack和queue的经典算法题来练习练习。
先给上题目链接：
155. 最小栈 - 力扣（LeetCode）
https://leetcode.cn/problems/min-stack/description/栈的压入、弹出序列_牛客题霸_牛客网https://www.nowcoder.com/practice/d77d11405cc7470d82554cb392585106?tpId=13&&tqId=11174&rp=1&ru=/activity/oj&qru=/ta/coding-interviews/question-ranking102. 二叉树的层序遍历 - 力扣（LeetCode）https://leetcode.cn/problems/binary-tree-level-order-traversal/description/依旧是建议大家先去自己动手练习练习哦。
155. 最小栈：
那么这道题，它难吗？难吗？力扣给出的是中等难度，那么它真的就是有那么难吗，哈哈，其实只要我们相通步骤，一下子就能理解了，我们先看题目：
题意分析：
一、题意拆解
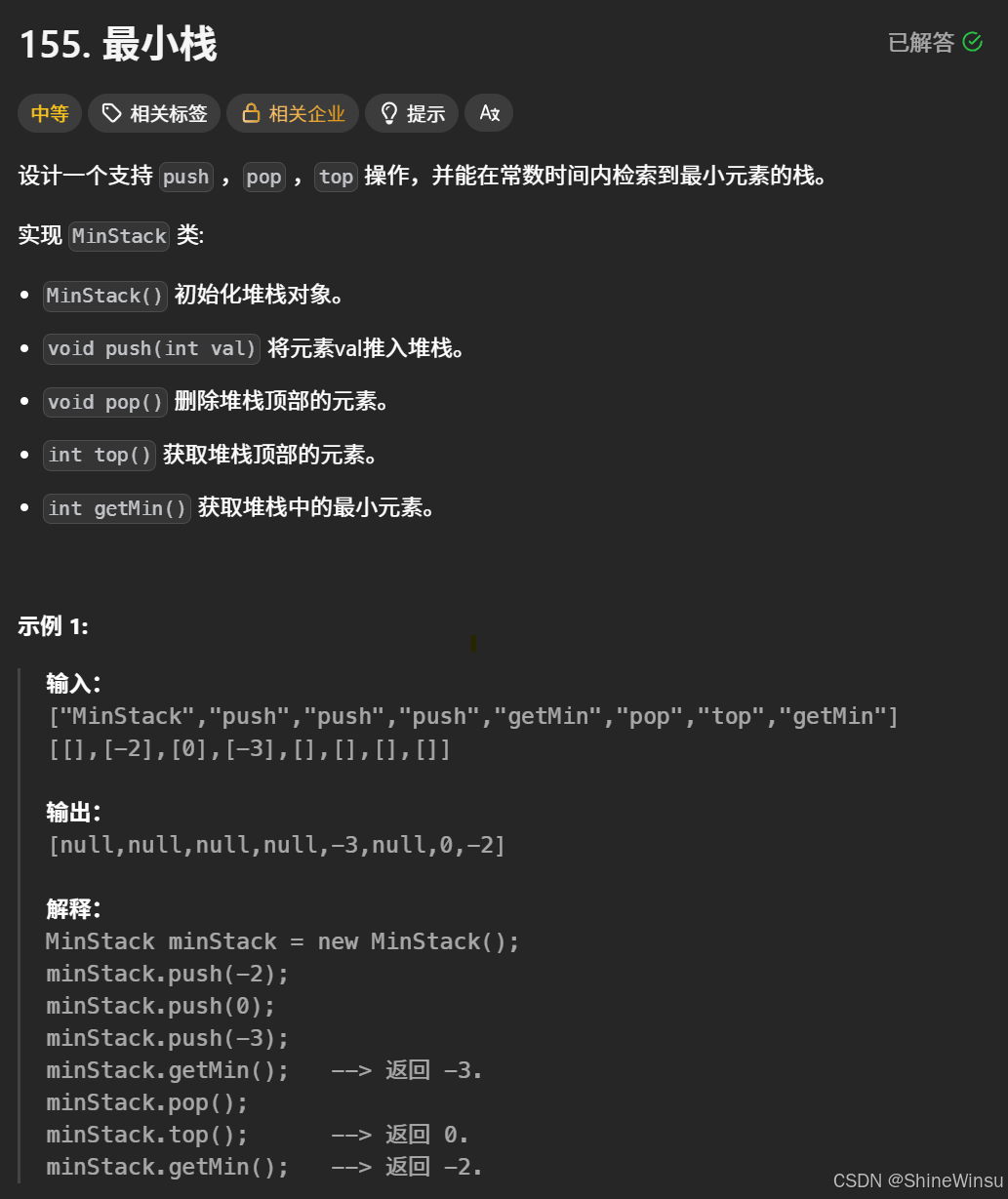
题目要求实现一个 MinStack 类，包含以下操作：
MinStack()：初始化栈对象。void push(int val)：将元素val压入栈。void pop()：删除栈顶元素。int top()：获取栈顶元素。int getMin()：获取栈中的最小元素，且需在常数时间内完成。
二、核心约束
- 时间复杂度 ：
getMin、push、pop、top操作都需满足 O(1) 时间复杂度。 - 空间复杂度：允许额外的空间开销（通常通过辅助数据结构实现）。
三、示例逻辑分析
以示例 1 为例，逐步拆解操作流程：
MinStack minStack = new MinStack()：初始化空栈。minStack.push(-2)：栈变为[-2]，当前最小值为-2。minStack.push(0)：栈变为[-2, 0]，当前最小值仍为-2。minStack.push(-3)：栈变为[-2, 0, -3]，当前最小值更新为-3。minStack.getMin()：返回当前最小值-3。minStack.pop()：删除栈顶元素-3，栈变为[-2, 0]，最小值回退为-2。minStack.top()：返回栈顶元素0。minStack.getMin()：返回当前最小值-2。
解析：
核心问题：如何快速获取最小值？
常规的栈只能高效支持push（入栈）、pop（出栈）、top（取栈顶）操作，但要获取栈中最小值，通常需要遍历整个栈（时间复杂度O(n)），无法满足 "常数时间" 的要求。
这个解法的关键是引入一个 "辅助栈"（最小栈） ，专门记录当前栈中元素的最小值。通过两个栈的配合，让getMin操作可以直接读取辅助栈的栈顶，实现O(1)时间复杂度。
具体设计：双栈协同工作
我们需要两个栈：
- 主栈（
st） ：存储所有入栈的元素，负责常规的push、pop、top操作。 - 最小栈（
minst）：存储 "当前主栈中所有元素的最小值"，其栈顶始终是主栈的最小值。
各操作的逻辑详解
1. 初始化（MinStack()）
无需手动初始化，因为st和minst都是stack类型，编译器会自动调用它们的默认构造函数，初始化为空栈。
2. 入栈（push(int val)）
往主栈中添加元素时，需要同步维护最小栈，确保其栈顶始终是当前最小值。具体逻辑：
- 先将
val压入主栈st（正常存储元素）。 - 再判断是否需要更新最小栈
minst：- 若
minst为空（说明是第一个入栈元素），直接将val压入minst（此时val就是唯一元素，也是最小值）。 - 若
val小于或等于minst的栈顶元素（说明val是新的最小值，或与当前最小值相等），则将val压入minst（更新最小值记录）。 - 若
val大于minst的栈顶元素（说明当前最小值不变），则minst不操作。
- 若
例子：
- 第一次
push(-2)：st变为[-2]，minst为空，所以minst也压入-2，minst变为[-2]（此时最小值是-2）。 - 第二次
push(0)：st变为[-2, 0]，0大于minst的栈顶-2，所以minst不变（仍为[-2]，最小值还是-2）。 - 第三次
push(-3)：st变为[-2, 0, -3]，-3小于minst的栈顶-2，所以minst压入-3，minst变为[-2, -3]（此时最小值是-3）。
3. 出栈（pop()）
从主栈中删除元素时，需要同步检查是否影响最小值，确保最小栈的栈顶仍是当前最小值。具体逻辑：
- 先判断主栈
st的栈顶元素是否与最小栈minst的栈顶元素相等：- 若相等（说明当前要删除的元素就是最小值），则
minst也需要出栈（删除旧的最小值记录）。 - 若不相等（说明删除的元素不是最小值，当前最小值不变），则
minst不操作。
- 若相等（说明当前要删除的元素就是最小值），则
- 最后将主栈
st的栈顶元素出栈。
例子 ：接上面的场景，st为[-2, 0, -3]，minst为[-2, -3]：
- 执行
pop()：主栈st的栈顶是-3，与minst的栈顶-3相等，所以minst也出栈（变为[-2]）；st出栈后变为[-2, 0]。此时最小值恢复为-2。
4. 取栈顶（top()）
直接返回主栈st的栈顶元素即可，因为st完整存储了所有元素的入栈顺序。
例子 ：上面pop()后，st为[-2, 0]，top()返回0。
5. 取最小值（getMin()）
直接返回最小栈minst的栈顶元素即可，因为minst的栈顶始终记录着当前主栈中所有元素的最小值。
例子：
- 第三次
push后，minst的栈顶是-3，getMin()返回-3。 pop()后，minst的栈顶是-2，getMin()返回-2。
设计的巧妙之处
- 时间效率 ：所有操作（
push、pop、top、getMin）的时间复杂度都是O(1)，因为仅涉及栈的入栈 / 出栈或取栈顶，无需遍历。 - 空间换时间 ：通过额外的
minst栈存储最小值记录，用O(n)的空间复杂度（最坏情况下，每个元素都入minst）换来了O(1)的时间效率。 - 处理重复最小值 ：
push时用 "小于等于" 判断（而非 "小于"），确保当有多个相同的最小值时，minst会同步记录，避免pop时误删最小值（例如连续push(2, 2)，minst会记录[2, 2]，pop一次后minst仍有2，保证最小值正确）。
怎么样大家，其实只要大家画个图，一下子就能理解了，下面我就给出完整代码：
cpp
class MinStack {
public:
// 构造函数：初始化MinStack对象
// 无需手动初始化成员变量，因为stack类会自动调用其默认构造函数，创建空栈
MinStack() {
// 编译器会自动为st和minst调用stack的默认构造函数，初始化为空栈
}
// 入栈操作：将元素val压入栈中，并维护最小栈
void push(int val) {
st.push(val); // 先将元素压入主栈st，保证所有元素的存储顺序
// 维护最小栈minst的核心逻辑：
// 1. 若最小栈为空（说明是第一个入栈元素），必须将当前元素压入minst（此时它就是最小值）
// 2. 若当前元素小于等于最小栈的栈顶元素（说明当前元素是新的最小值，或与最小值相等），则压入minst
// 注意：这里用<=而非<，是为了处理重复最小值的情况（例如连续入栈2、2，minst需同步记录，避免pop时误删）
if(minst.empty() || val <= minst.top()) {
minst.push(val);
}
// 若当前元素大于minst.top()，则minst不操作（当前最小值不变）
}
// 出栈操作：删除栈顶元素，并同步更新最小栈
void pop() {
// 检查主栈的栈顶元素是否与最小栈的栈顶元素相同：
// 若相同，说明当前要删除的元素就是最小值，因此最小栈也需要出栈（移除该最小值记录）
if(st.top() == minst.top()) {
minst.pop();
}
// 无论是否影响最小值，主栈都需要正常删除栈顶元素
st.pop();
}
// 获取栈顶元素：直接返回主栈的栈顶元素（主栈保存了所有元素的顺序）
int top() {
return st.top();
}
// 获取当前栈中的最小值：直接返回最小栈的栈顶元素（minst的栈顶始终是当前最小值）
int getMin() {
return minst.top();
}
private:
stack<int> st; // 主栈：负责存储所有入栈元素，维护正常的栈操作顺序
stack<int> minst; // 最小栈：专门记录当前主栈中元素的最小值，其栈顶始终是主栈的最小值
// 最小栈的设计逻辑：仅在主栈出现更小（或相等）的元素时才入栈，确保高效获取最小值
};那么我在这里再补充一下为什么当新的值等于栈的最小值的时候，我们也要去压入最小栈：
说明：
在push操作中，当val等于minst的栈顶元素时也要压入最小栈，核心原因是确保pop操作后，最小栈仍能正确记录剩余元素的最小值，尤其是在存在多个相同最小值的场景下。
举个具体例子说明：
假设我们连续入栈两个相同的最小值2：
-
第一次
push(2)：- 主栈
st变为[2]，最小栈minst为空，所以minst压入2，此时minst = [2]。
- 主栈
-
第二次
push(2)：- 主栈
st变为[2, 2]，val=2等于minst的栈顶2，因此minst继续压入2，此时minst = [2, 2]。
- 主栈
为什么必须压入第二个2？
如果第二次push(2)时因为 "等于" 而不压入minst，minst会保持[2]。此时执行pop操作：
- 主栈
st弹出栈顶2，变为[2]。 - 由于主栈弹出的
2等于minst的栈顶2，minst也会弹出2，变为空栈。 - 此时调用
getMin()会试图访问空栈的栈顶，导致错误（或未定义行为）。
正确逻辑下的结果：
由于第二次push(2)时minst压入了2（minst = [2, 2]）：
- 第一次
pop：主栈弹出2变为[2]，minst也弹出2变为[2]。 - 此时
getMin()返回minst的栈顶2，正确反映剩余元素的最小值。
本质原因：
最小栈minst的栈顶不仅要记录 "当前最小值"，还要与主栈的元素数量和顺序形成 "对应关系" ------ 每一个主栈元素都隐含着一个 "当前状态的最小值"。当有多个相同的最小值时，每个最小值在主栈中都需要一个对应的记录在minst中，否则pop时会提前删除唯一的最小值记录，导致后续getMin()出错。
简单说："等于时压入" 是为了保证minst能正确 "跟踪" 主栈中所有最小值的出现次数，避免提前删除导致的错误。
JZ31 栈的压入、弹出序列：
OK大家，这道题还勉勉强强算的上是一道难度还行的题目，我们先看题目：
题意分析：
一、问题本质拆解
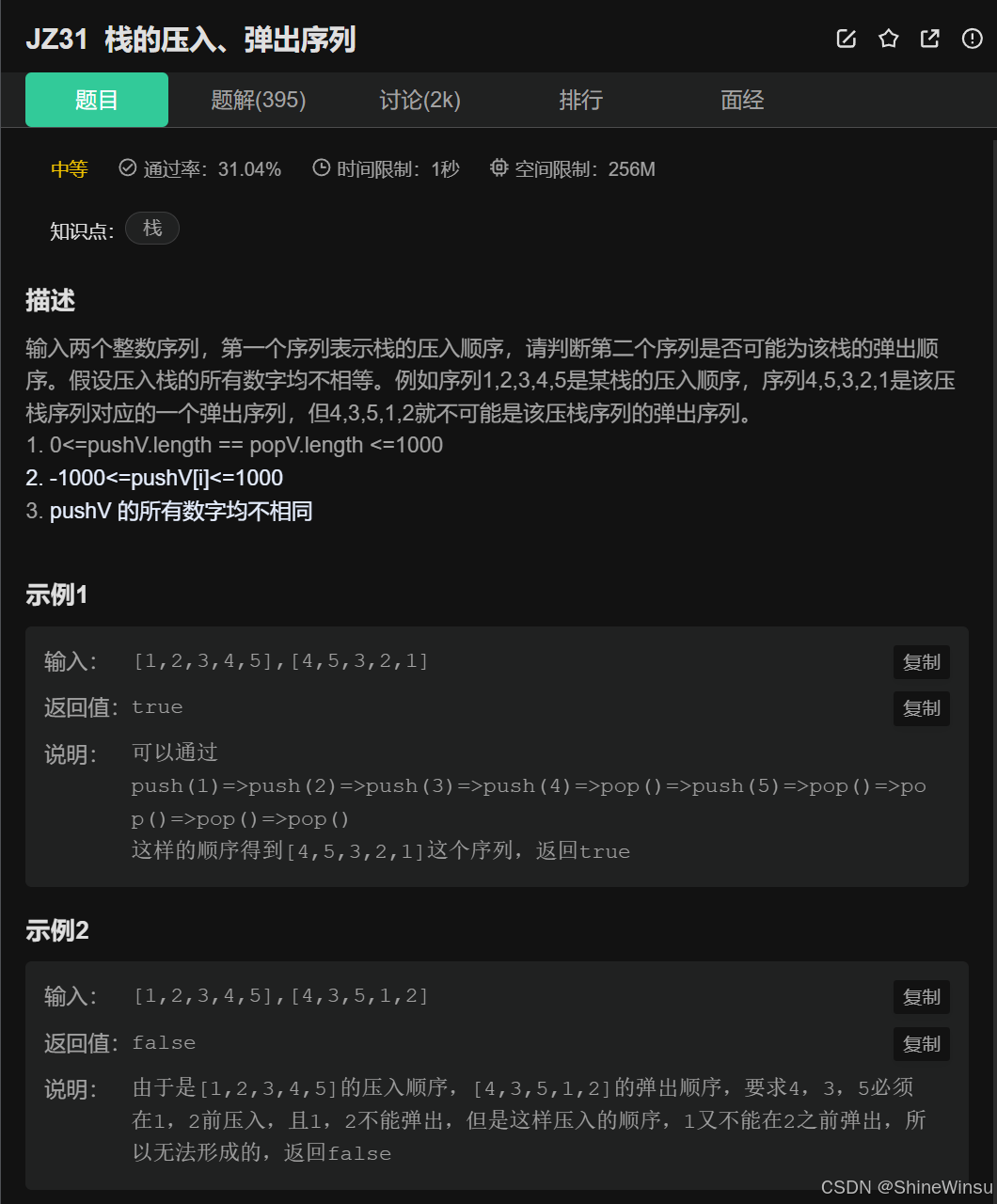
题目要求我们判断：给定一个 "压入序列"pushV，另一个 "弹出序列"popV是否是该栈的合法弹出顺序。
核心逻辑是模拟栈的 "压入 - 弹出" 过程，验证popV的每一个元素是否能在合理的时机从栈中弹出。
二、约束条件分析
- 长度约束 ：
pushV和popV的长度必须相等（否则直接不合法），且长度范围是0 ≤ 长度 ≤ 1000。 - 元素唯一性 ：
pushV中的所有数字均不重复（这是解题的关键前提，保证每个元素的弹出时机唯一）。 - 元素范围 ：
pushV中的元素取值范围是-1000 ≤ 元素 ≤ 1000。
三、示例逻辑深度解析
通过示例理解合法与非法弹出序列的区别：
示例 1：合法序列（pushV=[1,2,3,4,5]，popV=[4,5,3,2,1]）
模拟栈的操作流程：
- 压入
1→压入2→压入3→压入4→弹出4（匹配popV[0]）→压入5→弹出5（匹配popV[1]）→弹出3（匹配popV[2]）→弹出2（匹配popV[3]）→弹出1（匹配popV[4]）。 - 每一步弹出的元素都能与
popV的对应位置匹配，因此返回true。
示例 2：非法序列（pushV=[1,2,3,4,5]，popV=[4,3,5,1,2]）
模拟关键冲突点：
- 压入
1→压入2→压入3→压入4→弹出4（匹配popV[0]）→弹出3（匹配popV[1]）→压入5→弹出5（匹配popV[2]）。 - 此时栈中剩余元素为
[1,2]，但popV[3]是1，而栈顶是2------ 根据栈 "后进先出" 的特性，1在2之后压入，无法在2弹出前弹出，因此序列非法，返回false。
解析：
一、问题本质：栈的 "后进先出" 特性约束
栈的核心规则是 "后进先出（LIFO）"：最后压入的元素必须最先弹出。因此，一个合法的弹出序列popV必须满足：对于popV中的每个元素，它在弹出时必须是当前栈的栈顶元素，且在它之前弹出的元素要么是它之后压入的（符合 LIFO），要么是在它压入前就已存在于栈中（但需保证前面的元素未被提前弹出）。
例如：若pushV = [1,2,3]，则popV = [3,2,1]合法（每个元素都是栈顶时弹出）；但popV = [3,1,2]非法（1 在 2 之前压入，2 未弹出时 1 无法成为栈顶）。
二、核心解题思路：用辅助栈 "复现操作过程"
由于问题的核心是验证 "弹出顺序是否符合栈的操作规则"，最直接的方法是用一个辅助栈模拟真实的压入 - 弹出过程：
- 按
pushV的顺序，依次将元素压入辅助栈； - 每次压入后，立即检查栈顶元素是否与
popV当前需要弹出的元素一致； - 若一致，则弹出栈顶，并继续检查新栈顶是否与
popV下一个元素一致（可能连续弹出多个）； - 当所有元素都压入后，若辅助栈为空（所有元素都按
popV的顺序弹出），则popV合法；否则非法。
三、分步拆解：结合代码逻辑与实例
以pushV = [1,2,3,4,5]，popV = [4,5,3,2,1]（合法序列）和popV = [4,3,5,1,2]（非法序列）为例，逐步解析代码的执行逻辑。
1. 初始化与变量定义
- 辅助栈
st：模拟实际操作的栈，用于存储压入的元素。 - 指针
push：指向pushV中 "待压入" 的元素（初始值 0，从第一个元素开始）。 - 指针
pop：指向popV中 "待验证" 的弹出元素（初始值 0，从第一个元素开始）。
2. 外层循环：按pushV顺序压入元素
外层循环条件：push < pushV.size()（所有元素未压完时持续压入）。每次循环的核心逻辑：先压入元素，再检查是否可弹出。
步骤 1：压入元素的判断（内层第一个条件）
代码逻辑：if(st.empty()||st.top()!=popV[pop])含义：当辅助栈为空，或栈顶元素与popV当前待弹出元素（popV[pop]）不匹配时，需要继续压入pushV的下一个元素。
为什么这样判断？
- 若栈为空，必须先压入元素才能弹出（否则无元素可弹）；
- 若栈顶与
popV[pop]不匹配，说明当前栈顶不是要弹出的元素，需继续压入后续元素，直到栈顶匹配（或所有元素压完）。
步骤 2：压入元素并移动push指针
满足上述条件时，执行st.push(pushV[push]); ++push;，即压入pushV[push]，并将push指针后移（指向 next 待压入元素）。
步骤 3：弹出匹配的元素（内层循环）
代码逻辑：while(!st.empty()&&st.top()==popV[pop])含义：当栈不为空，且栈顶元素与popV[pop]匹配时，弹出栈顶，并将pop指针后移（验证下一个弹出元素），重复此过程直到栈顶不匹配或栈为空。
为什么用循环？ 可能存在 "连续弹出" 的情况：弹出当前栈顶后，新的栈顶可能仍与popV的下一个元素匹配（例如pushV = [1,2]，popV = [2,1]，弹出 2 后，栈顶 1 与popV[1]匹配，需继续弹出）。
3. 最终判断：辅助栈是否为空
当pushV所有元素都压入（push达到pushV.size()）后，若辅助栈st为空，说明所有元素都按popV的顺序弹出，popV合法；否则，栈中剩余元素无法按popV的顺序弹出，popV非法。
四、实例 1：合法序列pushV=[1,2,3,4,5]，popV=[4,5,3,2,1]
执行过程：
- 初始状态 ：
st空，push=0，pop=0。 - 第一次外层循环 ：栈空 → 压入
pushV[0]=1，push=1；栈顶 = 1≠popV[0]=4→ 退出内层循环。 - 第二次外层循环 ：栈顶 = 1≠4 → 压入
pushV[1]=2，push=2；栈顶 = 2≠4 → 退出内层循环。 - 第三次外层循环 ：栈顶 = 2≠4 → 压入
pushV[2]=3，push=3；栈顶 = 3≠4 → 退出内层循环。 - 第四次外层循环 ：栈顶 = 3≠4 → 压入
pushV[3]=4，push=4；栈顶 = 4=4 → 进入内层循环：弹出 4，pop=1；新栈顶 = 3≠popV[1]=5→ 退出内层循环。 - 第五次外层循环 ：栈顶 = 3≠5 → 压入
pushV[4]=5，push=5（pushV已压完）；栈顶 = 5=5 → 进入内层循环：弹出 5，pop=2；新栈顶 = 3=3 → 弹出 3，pop=3；新栈顶 = 2=2 → 弹出 2，pop=4；新栈顶 = 1=1 → 弹出 1，pop=5；栈空 → 退出内层循环。 - 最终 ：
push=5（循环结束），st为空 → 返回true（合法）。
五、实例 2：非法序列pushV=[1,2,3,4,5]，popV=[4,3,5,1,2]
执行过程（关键冲突点）：
- 前半程与合法序列一致：压入 1、2、3、4 后弹出 4（
pop=1），弹出 3（pop=2），压入 5 后弹出 5（pop=3）。 - 此时栈中剩余元素：
[1,2]（栈顶 = 2），popV[3]=1。 - 外层循环结束（
push=5），但栈顶 = 2≠1，且无法继续压入元素 → 辅助栈剩余[1,2]，不为空 → 返回false（非法）。
六、边界情况处理
- 空序列 ：
pushV和popV均为空 → 合法（返回true）；若一个空一个非空 → 非法（返回false）。 - 单元素序列 ：
pushV=[x]，popV=[x]→ 合法（压入后弹出）；popV=[y]（y≠x）→ 非法。 - 弹出顺序与压入顺序相同 ：
pushV=[1,2,3]，popV=[1,2,3]→ 合法（每次压入后立即弹出：压 1→弹 1，压 2→弹 2，压 3→弹 3）。
七、设计的核心细节与必要性
- 空栈判断（
!st.empty()） ：内层循环必须先判断栈不为空，再访问st.top()，否则会因 "访问空栈顶" 导致错误（例如pushV为空但popV非空时）。 - 连续弹出的循环 ：若不用循环，仅弹出一次就退出，会漏掉 "栈顶持续匹配" 的情况（例如
popV=[3,2,1]，弹出 3 后栈顶 2 仍匹配，需继续弹出）。 - 最终栈空的判据 ：栈空意味着所有元素都按
popV的顺序弹出，完全符合栈的操作规则；若栈非空，说明存在元素无法按popV的顺序弹出（违反 LIFO）。
总结
这个解法的本质是用辅助栈复现栈的真实操作流程 ，通过 "边压入边验证弹出" 的方式，实时检查popV的每一步是否符合栈的 "后进先出" 特性。其时间复杂度为O(n)（每个元素压入和弹出各一次），空间复杂度为O(n)（辅助栈最多存储n个元素），是解决此类问题的最优思路。理解这一过程的关键在于：栈的弹出只能在 "栈顶匹配" 时发生，而模拟操作是验证这种匹配性的最直接方式。
大家依旧是去画图，模拟过程，就很容易能理解到这道题目的，下面我就给出完整代码：
cpp
class Solution {
public:
/**
* 功能：判断弹出序列popV是否是压入序列pushV经过栈操作后的合法弹出顺序
* 原理：通过辅助栈模拟栈的压入-弹出过程，验证popV是否符合栈"后进先出"的特性
*
* @param pushV 压入序列（元素按此顺序压入栈）
* @param popV 弹出序列（需验证是否为合法的弹出顺序）
* @return bool 若popV是合法弹出序列则返回true，否则返回false
*/
bool IsPopOrder(vector<int>& pushV, vector<int>& popV) {
// 定义两个指针，分别指向pushV待压入的元素和popV待验证的弹出元素
int push = 0; // push指针：当前要压入辅助栈的元素在pushV中的索引
int pop = 0; // pop指针：当前要验证的弹出元素在popV中的索引
// 外层循环：按pushV的顺序将所有元素依次压入辅助栈（直到所有元素都压完）
while (push < pushV.size()) {
// 压入条件：当辅助栈为空，或栈顶元素与当前要弹出的元素（popV[pop]）不匹配时
// 说明需要继续压入元素，直到栈顶出现与popV[pop]匹配的元素
if (st.empty() || st.top() != popV[pop]) {
st.push(pushV[push]); // 将pushV[push]压入辅助栈
++push; // push指针后移，指向下次要压入的元素
}
// 内层循环：当辅助栈不为空，且栈顶元素与当前要弹出的元素（popV[pop]）匹配时
// 持续弹出栈顶元素，并验证下一个弹出元素（处理连续弹出的情况）
while (!st.empty() && st.top() == popV[pop]) {
// 注意：必须先判断栈不为空，再访问栈顶元素，否则会出现空栈访问错误
st.pop(); // 弹出栈顶元素（匹配当前弹出元素）
++pop; // pop指针后移，指向下次要验证的弹出元素
}
}
// 最终判断：当所有元素都压入后，若辅助栈为空，说明所有元素都按popV的顺序弹出（合法）
// 若栈不为空，说明存在元素无法按popV的顺序弹出（非法）
return st.empty();
}
private:
stack<int> st; // 辅助栈：模拟实际的栈操作过程，用于验证弹出序列的合法性
};不难。
102. 二叉树的层序遍历：
OK大家，二叉树，我们的老相好了，谁能忘记之前被二叉树折磨的死去活来的日子，哈哈哈，那么其实我们之前也是有讲过二叉树的层序遍历的，只不过没有练习，因为用C语言来完成的话，就太麻烦了，但是当我们学完了C嘎嘎之后，就简单很多了，所以我们就把这道题放在现在来讲，大家可以先去复习复习二叉树的层序遍历这一篇博客：对于数据结构：链式二叉树的超详细保姆级解析---下-CSDN博客https://blog.csdn.net/2503_92929084/article/details/152373693?spm=1011.2415.3001.5331
那么我们先看一下题目：
题意分析：
一、目标要求
给定二叉树的根节点 root，返回其节点值的层序遍历结果 。层序遍历的定义是：逐层地、从左到右访问所有节点，并将每一层的节点值单独存为一个子数组，最终返回由这些子数组成的二维数组。
二、遍历规则拆解
"逐层、从左到右" 的核心逻辑：
- "逐层"：树的第 1 层是根节点，第 2 层是根的左右子节点，第 3 层是第 2 层节点的左右子节点，以此类推。每一层的节点要单独存为一个子数组。
- "从左到右"：同一层内的节点，按照 "左子节点优先于右子节点" 的顺序访问。
三、示例逻辑验证
通过示例 1 理解具体遍历过程：
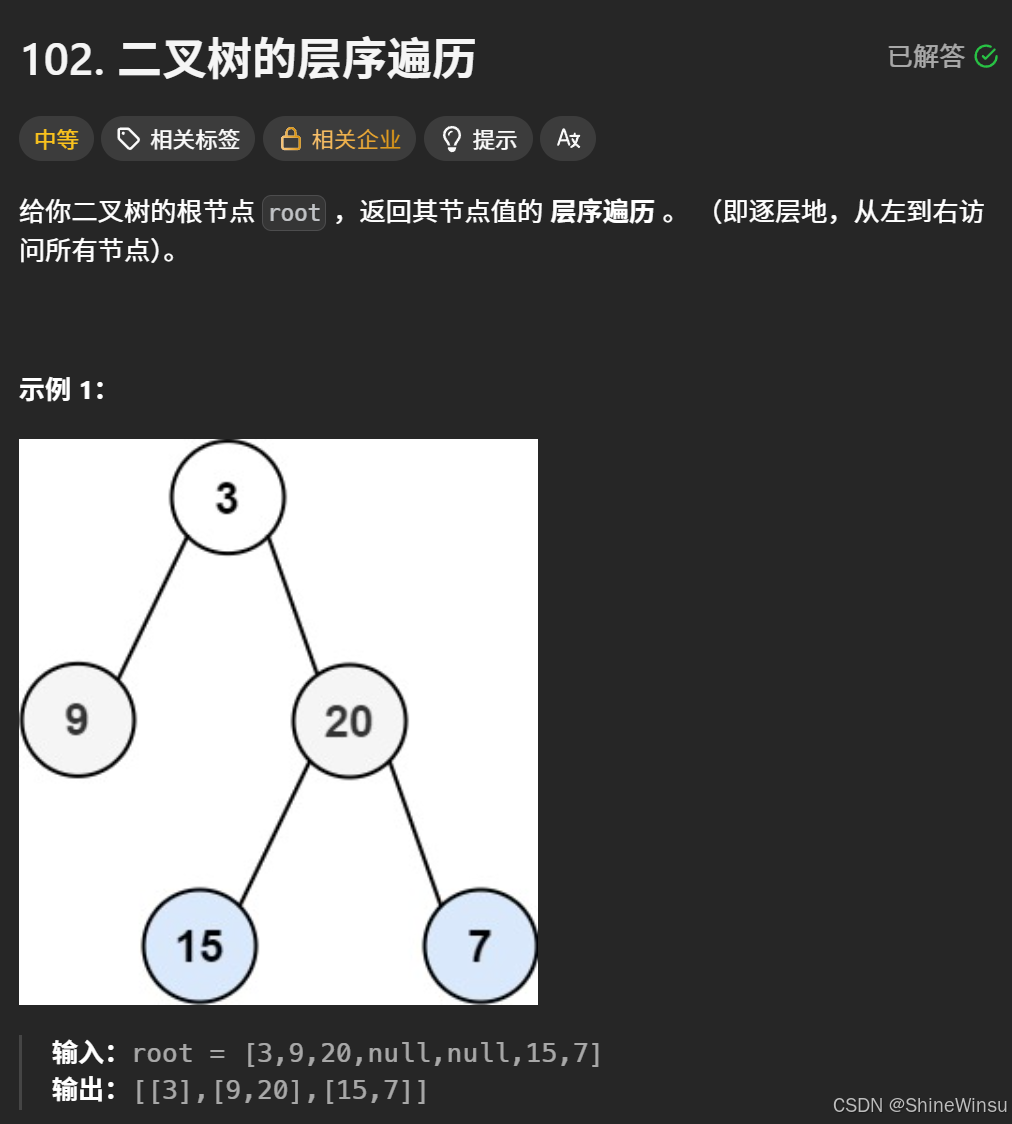
- 输入树结构：根节点
3（第 1 层）→ 左子节点9、右子节点20（第 2 层）→20的左子节点15、右子节点7（第 3 层）。 - 层序遍历结果：第 1 层
[3]→ 第 2 层[9,20]→ 第 3 层[15,7]→ 最终输出[[3],[9,20],[15,7]]。
四、边界条件分析
- 空树（
root = []） ：没有节点，返回空数组[]（如示例 3）。 - 单节点树（
root = [1]） ：只有一层，返回[[1]]（如示例 2）。 - 多层但部分层节点数不同：无论每层节点数多少，都需按层、从左到右收集（如示例 1 的 3 层结构）。
五、隐含约束
- 节点数量范围
[0, 2000]：需考虑性能，保证算法时间复杂度为O(n)（n为节点数），空间复杂度为O(n)（最坏情况存储一层所有节点）。 - 节点值范围
[-1000, 1000]：无需特殊数值处理，只需按顺序收集即可。
解析：
那么其实大家在看完之前写的那一篇关于层序遍历的解析之后，相信大家对于层序遍历的思路已经不陌生了，只不过相对于本题，题目还添加了一个要求，那就是把每一层的节点的数据都存进数组里面，也就是我们得需要一个二维数组，然后第二个vector里面每个空间就存储对应的层的每个节点的数据，这个大家看上面的题意解析也能知道。
所以呢，实现层序遍历是很简单的，我们可以用C嘎嘎中的现成的queue进行使用，但是问题就是我们要怎么去知道说，二叉树的每一层中，有几个节点呢？因为只有我们知道了这个，才能去传入数组中，不难不知道的话，我们又怎么知道要获取几次节点中存储的数据呢？这个是一个难点。
OK大家，我也不给大家卖关子了，我就直接说了吧，因为这个确实不是很好想到，其实每一层有几个节点，就是看当我们取完上一次后的所有节点之后的队列的数据个数，就是这样子，我给大家一些例子帮助大家理解：
例子 1：三层二叉树（对应题目示例 1 的树）
树结构：
cpp
3 （第1层，1个节点）
/ \
9 20 （第2层，2个节点）
/ \
15 7 （第3层，2个节点）队列操作流程：
- 初始状态 ：队列中只有根节点
3，此时队列大小为1→ 说明第 1 层有 1 个节点 。- 处理这 1 个节点：将
3存入第 1 层的子数组[3]，然后将其左右子节点9、20入队。
- 处理这 1 个节点：将
- 处理第 2 层前 ：队列中是
[9, 20]，队列大小为2→ 说明第 2 层有 2 个节点 。- 依次处理这 2 个节点：将
9存入第 2 层子数组，9无左右子节点（不操作）；将20存入第 2 层子数组，然后将其左右子节点15、7入队。
- 依次处理这 2 个节点：将
- 处理第 3 层前 ：队列中是
[15, 7]，队列大小为2→ 说明第 3 层有 2 个节点 。- 依次处理这 2 个节点：将
15存入第 3 层子数组，15无左右子节点；将7存入第 3 层子数组，7无左右子节点。
- 依次处理这 2 个节点：将
- 最终结果 ：
[[3], [9,20], [15,7]]，与题目示例 1 的输出一致。
例子 2：单节点树（对应题目示例 2）
树结构：
cpp
1 （第1层，1个节点）队列操作流程：
- 初始状态 ：队列中只有根节点
1，队列大小为1→ 说明第 1 层有 1 个节点 。- 处理这 1 个节点：将
1存入第 1 层子数组[1]，1无左右子节点（不操作）。
- 处理这 1 个节点：将
- 最终结果 ：
[[1]]，与题目示例 2 的输出一致。
例子 3：空树（对应题目示例 3）
树结构：无节点（root = []）。
队列操作流程：
- 初始时队列为空，直接返回空数组
[]，与题目示例 3 的输出一致。
核心逻辑总结
在层序遍历中，每一层的节点数等于 "处理该层前队列的大小"。因为队列的特性是 "先进先出"，当我们处理某一层时，队列中恰好存储了该层的所有节点（上一层的节点已被处理，且它们的子节点已入队）。通过读取 "处理前的队列大小"，就能精确知道当前层需要处理多少个节点，从而将这些节点的数值收集到同一个子数组中，实现 "分层存储" 的要求。
怎么样大家，在知道了这个之后，是不是顿时感觉自己茅塞顿开，脑子嘎嘎的爽，嘎嘎的清醒呢？
其实还是需要大家去不断模拟这个过程，大家才会真正的理解到这个意思，那么当大家理解到这个意思了之后，写出代码也是手拿把掐的事。
下面我就再总结一下本题的解答思路：
一、核心逻辑：用队列实现 "分层遍历"
二叉树的层序遍历要求 "先访问第 1 层（根节点），再访问第 2 层（根的左右子节点），以此类推，且同一层内从左到右访问"。队列的 "先进先出（FIFO）" 特性恰好适配这种需求：
- 先将第 1 层的节点放入队列，处理完第 1 层后，它们的子节点（第 2 层）会按顺序进入队列；
- 处理第 2 层时，队列中恰好只有第 2 层的节点，处理完后它们的子节点（第 3 层）再进入队列；
- 以此类推，通过 "记录当前层的节点数量"，就能精确区分每一层的节点，实现分层收集。
二、分步拆解：遍历流程的细节
整个算法可分为 "初始化→逐层处理→收集结果" 三个阶段，每个阶段的逻辑如下：
1. 初始化：准备队列和结果容器
- 结果容器 ：用二维数组
vv存储最终结果（每个子数组对应一层的节点值）；用临时数组ret存储当前层的节点值（处理完一层后清空，用于下一层）。 - 辅助队列 ：用队列
q存储待处理的节点（队列中始终只包含 "当前层及以下层" 的节点，且按层的顺序排列）。 - 边界处理 ：若根节点
root为空（空树），则直接返回空的vv；否则，先将根节点加入队列（作为第 1 层的初始节点）。
2. 逐层处理：用队列大小划分层级
当队列不为空时，循环处理每一层的节点，核心是通过 "队列大小" 确定当前层的节点数：
-
步骤 1：确定当前层的节点数 每进入外层循环（处理新的一层）时，用
levelsize记录当前队列的大小（levelsize = q.size()）。由于队列中此时的所有节点都是 "上一层节点的子节点"，即当前层的全部节点，因此levelsize就是当前层的节点总数。 -
步骤 2：遍历当前层的所有节点 用内层循环（循环
levelsize次）处理当前层的每个节点：- 取出队列的队头节点（当前层的一个节点），将其值存入临时数组
ret（收集当前层的节点值）； - 若该节点有左子节点，将左子节点加入队列（作为下一层的节点）；
- 若该节点有右子节点，将右子节点加入队列（作为下一层的节点）；
- 弹出队头节点（已处理完，从队列中移除），并将
levelsize减 1（当前层待处理节点数减少）。
- 取出队列的队头节点（当前层的一个节点），将其值存入临时数组
-
步骤 3：收集当前层的结果 当内层循环结束（
levelsize减为 0），说明当前层的所有节点已处理完毕，此时ret中存储的就是当前层的所有节点值。将ret加入二维数组vv，并清空ret（准备收集下一层的节点值）。
3. 终止条件：队列为空时返回结果
当外层循环结束（队列q为空），说明所有层的节点都已处理完毕，此时vv中已按顺序存储了每一层的节点值，直接返回vv即可。
三、实例验证：以三层二叉树为例
用经典的三层二叉树（根节点 3，第 2 层 9 和 20，第 3 层 15 和 7）演示整个流程：
树结构：
cpp
3 （第1层）
/ \
9 20 （第2层）
/ \
15 7 （第3层）遍历流程：
-
初始化 ：根节点 3 不为空，加入队列
q，此时q = [3]；vv和ret均为空。 -
处理第 1 层：
- 外层循环：队列非空，
levelsize = q.size() = 1（第 1 层有 1 个节点）。 - 内层循环（1 次）：
- 队头是 3，将 3 的值加入
ret（ret = [3]）； - 3 的左子节点 9、右子节点 20 存在，加入队列，
q变为[9, 20]； - 弹出 3，
levelsize减为 0，内层循环结束。
- 队头是 3，将 3 的值加入
- 收集结果：
vv加入ret（vv = [[3]]），清空ret（ret = []）。
- 外层循环：队列非空，
-
处理第 2 层：
- 外层循环：队列非空（
q = [9, 20]），levelsize = 2（第 2 层有 2 个节点）。 - 内层循环（2 次）：
- 第 1 次：队头是 9，值加入
ret（ret = [9]）；9 无左右子节点，队列不变（q = [20]）；弹出 9，levelsize = 1。 - 第 2 次：队头是 20，值加入
ret（ret = [9, 20]）；20 的左子节点 15、右子节点 7 加入队列，q变为[15, 7]；弹出 20，levelsize = 0，内层循环结束。
- 第 1 次：队头是 9，值加入
- 收集结果：
vv加入ret（vv = [[3], [9, 20]]），清空ret。
- 外层循环：队列非空（
-
处理第 3 层：
- 外层循环：队列非空（
q = [15, 7]），levelsize = 2（第 3 层有 2 个节点）。 - 内层循环（2 次）：
- 第 1 次：队头是 15，值加入
ret（ret = [15]）；15 无左右子节点，队列变为[7]；弹出 15，levelsize = 1。 - 第 2 次：队头是 7，值加入
ret（ret = [15, 7]）；7 无左右子节点，队列变为空；弹出 7，levelsize = 0，内层循环结束。
- 第 1 次：队头是 15，值加入
- 收集结果：
vv加入ret（vv = [[3], [9, 20], [15, 7]]），清空ret。
- 外层循环：队列非空（
-
终止 ：队列为空，外层循环结束，返回
vv，即层序遍历的结果。
四、边界情况处理
- 空树（
root = nullptr） ：队列初始为空，外层循环不执行，直接返回空的vv（[]）。 - 单节点树（只有根节点） ：队列初始为
[root]，处理 1 层后队列空，vv为[[root->val]]。 - 斜树（所有节点只有左 / 右子节点） ：例如 "1→2→3→4"（每层 1 个节点），遍历后
vv为[[1], [2], [3], [4]]，仍能正确分层。
总结
这个算法的核心是用队列保存待处理节点，通过 "队列大小" 确定当前层的节点数 ，从而实现 "逐层、从左到右" 的遍历。每一层的节点处理完毕后，它们的子节点恰好按顺序进入队列，保证了下一层的处理顺序。整个过程的时间复杂度为O(n)（每个节点入队、出队各一次），空间复杂度为O(n)（队列最多存储一层的所有节点，最坏情况为满二叉树的最后一层，约n/2个节点），高效适配层序遍历的需求。
下面是完整代码：
cpp
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val; // 节点存储的值
* TreeNode *left; // 左子节点指针
* TreeNode *right; // 右子节点指针
* // 构造函数：分别对应无参、带值、带值及左右子节点的初始化
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
/**
* 功能：实现二叉树的层序遍历，返回每一层节点值组成的二维数组
* 层序遍历规则：逐层、从左到右访问所有节点，每一层的节点值单独作为一个子数组
* @param root 二叉树的根节点指针（若为空则表示空树）
* @return vector<vector<int>> 层序遍历的结果，外层数组的每个元素对应一层的节点值
*/
vector<vector<int>> levelOrder(TreeNode* root)
{
vector<vector<int>> vv; // 最终结果：存储所有层的节点值（外层数组按层序排列）
vector<int> ret; // 临时数组：存储当前层的节点值（处理完一层后清空复用）
// 初始化：若根节点不为空，将其加入队列（根节点是第1层的起始节点）
if(root != nullptr)
{
q.push(root);
}
// 外层循环：只要队列不为空，说明还有未处理的层，继续遍历
while(!q.empty())
{
// 关键：记录当前层的节点数量（队列中此时的元素都是当前层的节点）
levelsize = q.size();
// 内层循环：处理当前层的所有节点（循环次数=当前层节点数levelsize）
while(levelsize)
{
// 1. 收集当前节点的值到临时数组ret（当前层的节点值）
ret.push_back(q.front()->val);
// 2. 将当前节点的左右子节点加入队列（作为下一层的节点，保证从左到右顺序）
if(q.front()->left != nullptr) // 左子节点存在则入队
{
q.push(q.front()->left);
}
if(q.front()->right != nullptr) // 右子节点存在则入队
{
q.push(q.front()->right);
}
// 3. 弹出当前节点（已处理完毕，从队列中移除）
q.pop();
// 4. 当前层待处理节点数减1（直到levelsize=0，当前层处理完毕）
--levelsize;
}
// 内层循环结束：当前层所有节点值已存入ret，将其加入最终结果vv
vv.push_back(ret);
// 清空临时数组ret，准备收集下一层的节点值
ret.clear();
}
// 返回层序遍历的结果
return vv;
}
private:
queue<TreeNode*> q; // 辅助队列：存储待处理的节点，利用"先进先出"特性保证层序和左右顺序
size_t levelsize; // 记录当前层的节点数量：用于控制内层循环，确保只处理当前层的节点
};还是不难的吧大家。
结语：
亲爱的小伙伴们，当你们看到这里时，相信对栈、队列在算法题中的应用已经有了更深入的理解。从 "最小栈" 中双栈协同的巧妙，到 "栈的压入弹出序列" 中模拟操作的严谨，再到 "二叉树层序遍历" 中队列分层的智慧，每一道题都像一把钥匙，为我们打开了数据结构 "活用" 的大门。
其实，学习编程的过程就像在搭建一座大厦。栈和队列这些基础容器是地基里的钢筋，看似简单，却支撑着无数复杂的算法逻辑。我们今天做的每一道题，都是在亲手打磨这些钢筋 ------ 理解它们的特性，熟悉它们的接口，最终让它们成为我们解决问题时 "召之即来、来之能战" 的利器。
可能有小伙伴会说："这些题看起来不难，但我自己做的时候总是想不到思路。" 别怕，这太正常了。就像 "最小栈" 里的辅助栈设计，第一次接触时谁会立刻想到 "用另一个栈记录最小值" 呢？又比如层序遍历中 "用队列大小划分层级"，这种将 "隐性规律" 转化为 "显性操作" 的思路，本就需要多思考、多总结才能内化。
记住，算法的本质是 "解决问题的思路"，而数据结构是实现思路的 "工具"。我们今天练习的三道题，核心都不是 "会不会用栈和队列"，而是 "为什么要用它们"：因为栈的 "后进先出" 特性，才能高效记录最小值的变化；因为队列的 "先进先出" 特性，才能天然适配层序遍历的顺序。理解了 "特性与问题的匹配度"，才算真正打通了 "数据结构" 与 "算法" 之间的任督二脉。
在练习的过程中，画图和模拟永远是最好的帮手。比如分析 "栈的压入弹出序列" 时，拿一张纸画出每次压入、弹出后栈的状态，就能直观地看到序列是否合法；思考 "层序遍历" 时，写下每一步队列中的元素，就能清晰地发现 "队列大小即当前层节点数" 的规律。这些看似 "笨办法" 的操作，恰恰是培养算法思维的捷径 ------ 毕竟，再复杂的逻辑，拆解成一步步具体的操作后，都会变得清晰起来。
还要提醒大家，不要害怕重复。一道题今天看懂了，过几天可能又会模糊；一个思路今天觉得 "妙啊"，下次遇到类似问题可能还是想不到。这时候，不妨拿出代码再敲一遍，对着注释逐行分析，甚至尝试用不同的方式实现（比如 "最小栈" 能不能用单栈实现？"层序遍历" 能不能用递归做？）。重复不是机械劳动，而是让知识从 "看懂" 到 "会用" 的必经之路。
编程的世界里，没有谁是天生的 "解题高手"。那些看似轻松就能写出优雅代码的人，背后都是一次次试错、一遍遍复盘的积累。就像我们今天讨论的三道题，它们都是面试中的经典题目，之所以经典，不是因为难度有多高，而是因为它们精准地考察了对数据结构特性的理解和灵活运用能力。把这些基础题吃透，再面对更复杂的问题时，才能有 "以不变应万变" 的底气。
最后，想对每一位坚持学习的小伙伴说：编程的路上，慢就是快。不要急于追求 "刷多少题"，而要追求 "每道题学到了什么"。当你真正理解了栈和队列如何在这些题目中发挥作用，当你能独立分析出 "为什么用这个数据结构"，你就已经比昨天的自己进步了一大步。
未来还有更多有趣的算法和数据结构等着我们去探索，比如用堆解决_topK 问题_，用哈希表优化查找效率，用图论分析复杂的关系网络...... 但请相信，今天打下的基础，会成为我们探索更远世界的底气。
所以，别停下脚步。遇到不懂的题就多画一张图，敲错的代码就多调试一次，模糊的概念就多查一次资料。每一次小小的努力，都会在未来的某一天，让你突然发现：曾经觉得难如登天的问题，现在看来不过是 "纸老虎"。
加油，屏幕前的每一位追光者。编程的世界里，热爱与坚持，永远是最强大的算法。我们下一道题再见！