本节目标:
1 . 利用昨日明确返回值,设计核心任务------完成递归方法(递归_二叉树_48 . 二叉树最近公共祖先查找-CSDN博客)
2 . 初步进阶:递归嵌套
3 . 最佳方法:前缀和(哈希表),明白:什么叫找祖先结点
题目介绍
给定一个二叉树的根节点 root ,和一个整数 targetSum ,求该二叉树里节点值之和等于 targetSum 的 路径 的数目。
路径 不需要从根节点开始,也不需要在叶子节点结束,但是路径方向必须是向下的(只能从父节点到子节点)。
示例 1:
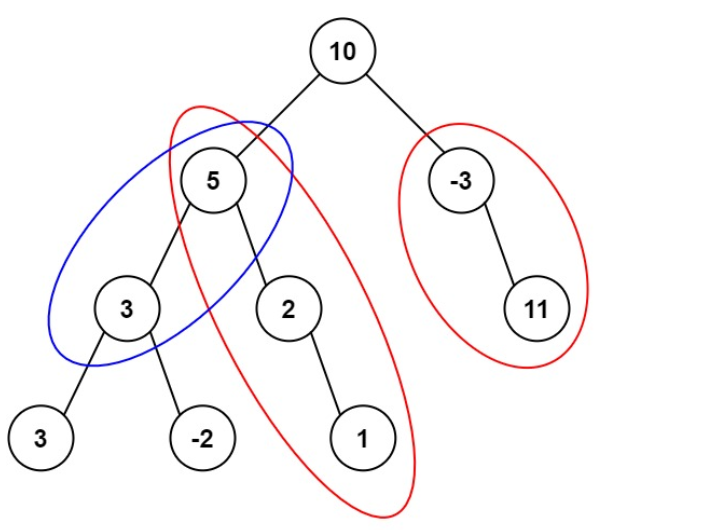
**输入:**root = [10,5,-3,3,2,null,11,3,-2,null,1], targetSum = 8
**输出:**3
**解释:**和等于 8 的路径有 3 条,如图所示。
示例 2:
**输入:**root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
**输出:**3
cpp
class Solution {
public:
int pathSum(TreeNode* root, int targetSum) {
}
};本文(除尾末代码 约 4000 字,阅读+思考约 17min
检验答案网址:437. 路径总和 III - 力扣(LeetCode)
解析
1 . 本题需求很明确:又是二叉树------递归,跑不了
2 . 给你一棵二叉树(用本树根节点代表),让你返回有多少连续父子结点和为targetSum(返回值为int)
3 . 递归方法为延续在昨日基础上有所进阶,进阶部分为嵌套递归
4 . 而最佳方法则是另一重点------前缀和
递归------嵌套递归
1 . 我们按照以往解决递归的方式方法:递归------核心任务和递归出口
a . 核心任务:对当前树的操作------联系传入参数和返回值设计
b . 递归出口:对传入参数的合法性进行判断
2 . 核心任务:
a . 我们能明确此处int (返回值)的含义:当前根节点所含连续结点和值为target的数量。比如:
以5为根节点的树,它应该返回2:左子树+右子树
以5为根节点的树,它应该返回1:左子树+右子树
而以10为树,应该返回3:左子树+右子树
b . 那么可以推测:
i ) 当面对当前树:我们要做的返回以本树得知的所有情况,return left_result + right_result
ii)但是,怎么判断连续的父子结点和为target------我们需要史官记录:跟随每一个函数同步更新
iii) 什么时候更新path 呢?path记录了从起点到本结点的和------自然是进入一个结点就path += root->val
代码已经跃然纸上:
cpp
int dfs(TreeNode* root,int targetSum,int path)
{
path += root->val;// path记录
int count = 0;
if(path == targetSum) // 如果遇到第一个终点,为什么说第一个终点:你保不齐后面来 0 -1 1这种正负连续抵消序列
count = 1;
int left_res = dfs(root->left,targetSum,path);
int right_res = dfs(root->right,targetSum,path);
return count+left_res+right_res;
}3 . 但是根据题意,"路径 不需要从根节点开始,也不需要在叶子节点结束,但是路径方向必须是向下的(只能从父节点到子节点)"还未体现
4 . 我们写的这一段dfs解决了什么呢?统计了以root为根的树所得知的所有路径数量。
5 . 我们就差一个多起点逻辑:
不妨再跳出来一层,继续递归:
6 . 这是主递归的接口,我们确定它的返回值含义:
cppclass Solution { public: int pathSum(TreeNode* root, int targetSum) { } };返回值:应该是全部结点为起点得到的情况
7 . 核心任务:计算出以当前结点root为起点的所有情况(dfs),别忘了root还可以得到结点root->left 和 root->right
8 . 计算出当前结点的所有路径数量 ------正是dfs()
cpp
int pathSum(TreeNode* root, int targetSum) {
int current = dfs(root,targetSum,0);
int left_result = pathSum(root->left,targetSum);
int right_result = pathSum(root->right,targetSum);
return current+left_result+right_result;
}9 . 最后都加上递归出口:形成的完整代码
cpp
class Solution {
public:
int pathSum(TreeNode* root, int targetSum) {
if(root == nullptr)
return 0;
int current = dfs(root,targetSum,0);
int left_result = pathSum(root->left,targetSum);
int right_result = pathSum(root->right,targetSum);
return current+left_result+right_result;
}
int dfs(TreeNode* root,int targetSum,long long path)
{
if(root == nullptr)
return 0;
path += (root->val);
// if(path == targetSum)
// return 1;// 这不是终点
int count = (path == targetSum?1:0);
count += dfs(root->left,targetSum,path);// ?
count += dfs(root->right,targetSum,path);
return count;
}
};前缀和
1 . 本道题的最优方法:利用前缀和统计好每个结点到0的值

2 . 因为n不止一个,所以需要一个哈希表去映射mp[m_prefix - targetSum]得到n_prefix的出现次数
3 . 那么,找出两个结点之间和targetSum的结点个数,只需要统计一遍所有结点的前缀和。再在每一个结点里去寻找它的祖先个数m_prefix-targetSum;相加起来就完成了
4 . 为了严格保证祖先真的是本结点祖先,应该在mp[当前前缀和]++更新之前完成祖先个数的查找
5 . 统计每个结点的前缀和。不妨还是用递归:
cpp
int dfs(TreeNode* root,int targetSum,long long curr_pre,unordered_map<long long,int>& mp)
{
curr_pre += root->val;// 更新curr_pre 当前结点的前缀和
int count = 0;
if(mp.count(curr_pre-targetSum))// 统计合适的组合个数:find查找祖先是否存在
{
count = mp[curr_pre-targetSum];
}
mp[curr_pre]++;// 再向下遍历其他结点,root已经成为祖先------进祖先谱
dfs(root->left,targetSum,curr_pre,mp);
dfs(root->right,targetSum,curr_pre,mp);
mp[curr_pre]--;// 回溯,函数结束之时,会回到上层的dfs------撤销本次进族谱操作
}a . 需要知道当前结点(树),targetSum 。还需要一个能实时反映本节点前缀和的变量,以及方便查询的族谱------原接口设计不满足,自己设函数
b . 先是更新curr_pre 为自己的前缀和,再找自己的祖先个数------向下遍历其他结点,自己先进族谱
c. 再加递归出口 和 返回值:
cpp
int dfs(TreeNode* root,int targetSum,long long curr_pre,unordered_map<long long,int>& mp)
{
if(root == nullptr) return 0;
curr_pre += root->val;
int count = 0;
if(mp.count(curr_pre-targetSum))
{
count = mp[curr_pre-targetSum];
}
mp[curr_pre]++;
count += dfs(root->left,targetSum,curr_pre,mp);
count += dfs(root->right,targetSum,curr_pre,mp);
mp[curr_pre]--;
return count;
}6 . 主函数补充调用一下:
cpp
int pathSum(TreeNode* root, int targetSum) {
unordered_map<long long,int> mp;// 前缀和,次数
long long curr_pre = 0;
mp[0] = 1;// 初始化:根节点的祖先------其前缀和0. 路径条数为1------方便统计m_prefix == targetSum的情况
return dfs(root,targetSum,curr_pre,mp);
}
完整代码:
cpp
class Solution {
public:
int pathSum(TreeNode* root, int targetSum) {
unordered_map<long long,int> mp;// 前缀和,次数
long long curr_pre = 0;
mp[0] = 1;
return dfs(root,targetSum,curr_pre,mp);
}
int dfs(TreeNode* root,int targetSum,long long curr_pre,unordered_map<long long,int>& mp)
{
if(root == nullptr) return 0;
curr_pre += root->val;
int count = 0;
if(mp.count(curr_pre-targetSum))
{
count = mp[curr_pre-targetSum];
}
mp[curr_pre]++;
count += dfs(root->left,targetSum,curr_pre,mp);
count += dfs(root->right,targetSum,curr_pre,mp);
mp[curr_pre]--;
return count;
}
};作者有话说:
递归_二叉树快速掌握路线:
开篇
中阶
递归_二叉树_48 . 二叉树最近公共祖先查找-CSDN博客
进阶 本章
总结以及完整参考代码

cpp
class Solution {
public:
int pathSum(TreeNode* root, int targetSum) {
if(root == nullptr)
return 0;
int current = dfs(root,targetSum,0);
int left_result = pathSum(root->left,targetSum);
int right_result = pathSum(root->right,targetSum);
return current+left_result+right_result;
}
int dfs(TreeNode* root,int targetSum,long long path)
{
if(root == nullptr)
return 0;
path += (root->val);
// if(path == targetSum)
// return 1;// 这不是终点
int count = (path == targetSum?1:0);
count += dfs(root->left,targetSum,path);// ?
count += dfs(root->right,targetSum,path);
return count;
}
};
cpp
class Solution {
public:
int pathSum(TreeNode* root, int targetSum) {
unordered_map<long long,int> mp;// 前缀和,次数
long long curr_pre = 0;
mp[0] = 1;
return dfs(root,targetSum,curr_pre,mp);
}
int dfs(TreeNode* root,int targetSum,long long curr_pre,unordered_map<long long,int>& mp)
{
if(root == nullptr) return 0;
curr_pre += root->val;
int count = 0;
if(mp.count(curr_pre-targetSum))
{
count = mp[curr_pre-targetSum];
}
mp[curr_pre]++;
count += dfs(root->left,targetSum,curr_pre,mp);
count += dfs(root->right,targetSum,curr_pre,mp);
mp[curr_pre]--;
return count;
}
};