双指针算法详解：从原理到实战（含LeetCode经典例题）

say_fall2026-02-18 14:07

欢迎来到 s a y − f a l l 的文章 欢迎来到say-fall的文章 欢迎来到say−fall的文章

🌈 say-fall：个人主页 🚀 专栏：《手把手教你学会C++》 | 《C语言从零开始到精通》 | 《数据结构与算法》 | 《小游戏与项目》 💪 格言：做好你自己，才能吸引更多人，与他们共赢，这才是最好的成长方式。

前言：

基于数据结构的扎实基础，算法思想能够有效提升问题解决的效率。为此，我们开设一个专门的算法专栏，用来探讨各类算法题目的解决方案。

在算法学习的道路上，双指针是一种简洁、高效且应用广泛的解题思想，它并非局限于某一种特定的数据结构，而是一种通过设置两个"标记点"（指针），协同遍历、筛选或修改数据，从而简化问题复杂度的核心思路。无论是数组、链表的遍历处理，还是数值组合、环形问题的求解，双指针都能发挥其独特优势------相较于暴力枚举的多层循环，它往往能将时间复杂度从O(n²)优化至O(n)，大幅提升代码运行效率，同时让解题逻辑更清晰、代码更简洁易懂。
本文将系统拆解双指针算法的核心逻辑，按"快慢双指针""首尾双指针""快慢双指针解决环形问题"三大类别，结合LeetCode经典例题（如移动零、盛水最多的容器、三数之和、环形链表等），从算法思想、解题步骤、代码实现三个维度，手把手带你掌握双指针的用法。每道例题均搭配详细解析和优化思路，兼顾基础入门与进阶提升，帮助你真正理解双指针的核心逻辑。

文章目录

  • 前言：
  • 正文：
    • 零、什么是双指针
    • 一、快慢双指针
      • [0. 算法思想：](#0. 算法思想：)
      • [1. 双指针快排思想](#1. 双指针快排思想)
      • [2. 双指针移动零](#2. 双指针移动零)
      • [3. 复写零](#3. 复写零)
    • 三、首尾双指针
      • [0. 算法思想:](#0. 算法思想:)
      • [1. 双指针移动零](#1. 双指针移动零)
      • [2. 盛水最多的容器](#2. 盛水最多的容器)
      • [3. 两数之和](#3. 两数之和)
      • [4. 三数之和](#4. 三数之和)
      • [5. 有效三角形的个数](#5. 有效三角形的个数)
      • [6. 四数之和](#6. 四数之和)
    • 三、快慢双指针解决环形问题
      • [0. 算法思想：](#0. 算法思想：)
      • [1. 环形链表](#1. 环形链表)
      • [2. 快乐数](#2. 快乐数)

正文：

零、什么是双指针

需要说明的是，双指针并不局限于字面意义上的两个指针，而是通过标记两个目标点来简化问题的解决思路。接下来，我们通过具体实例深入解析这一算法。

一、快慢双指针

0. 算法思想：

前后快慢指针以慢指针为基准划分界限：慢指针左侧（包括其指向的元素）均小于等于基准值，右侧均大于基准值；或者是慢指针左或者右为同一元素。

1. 双指针快排思想

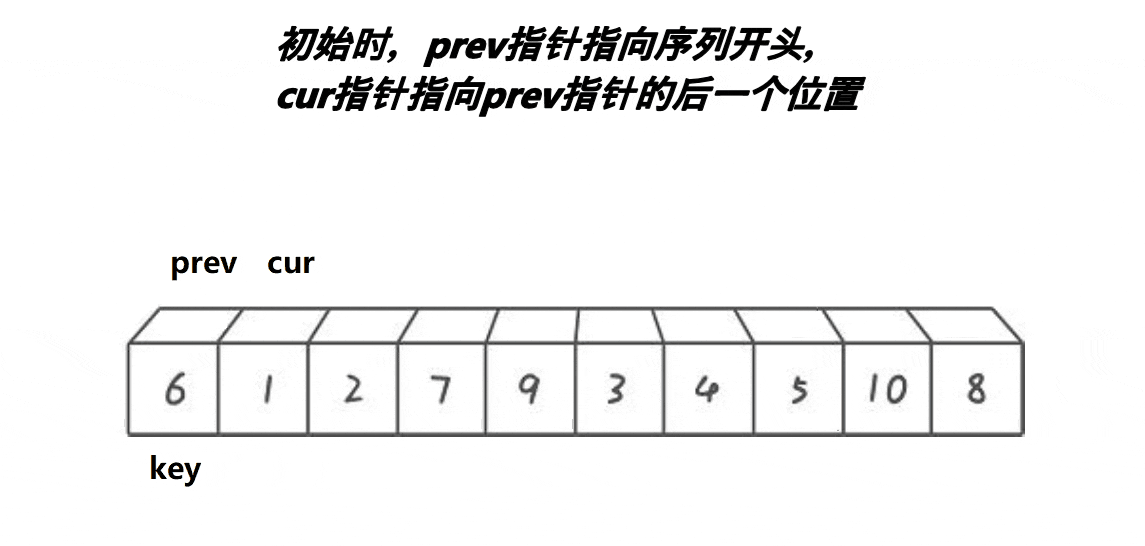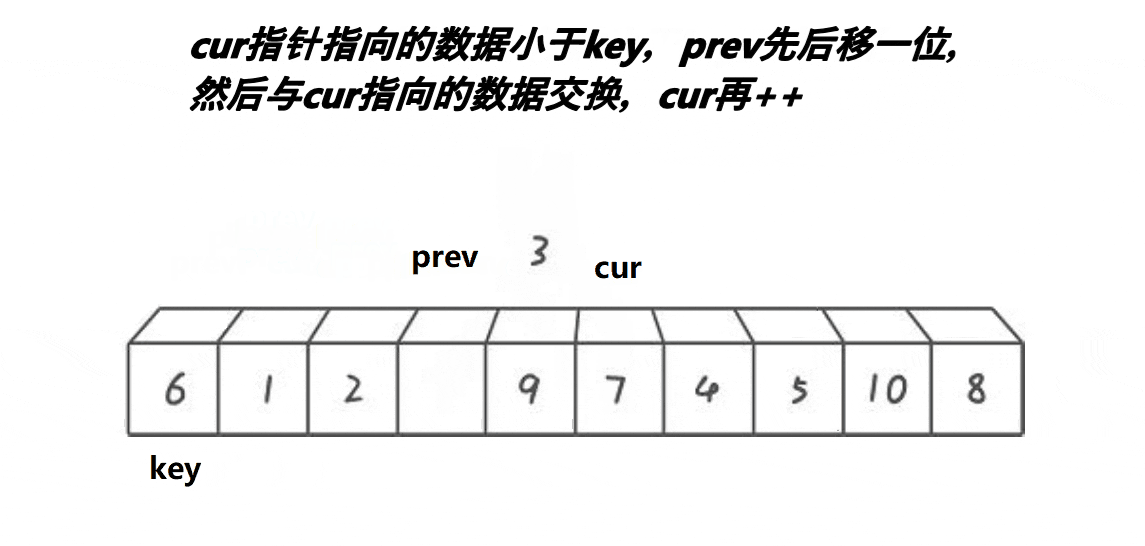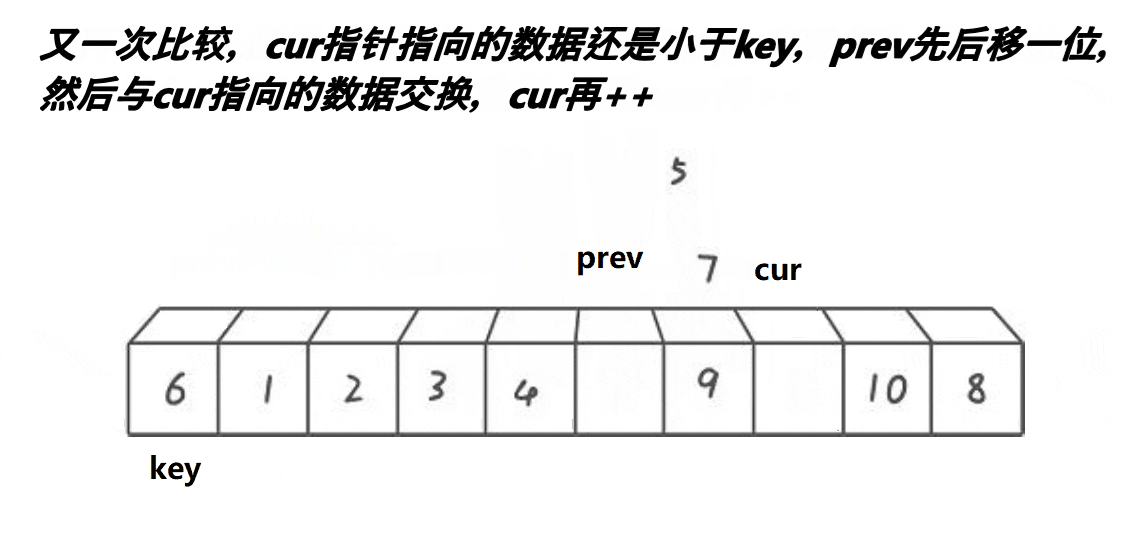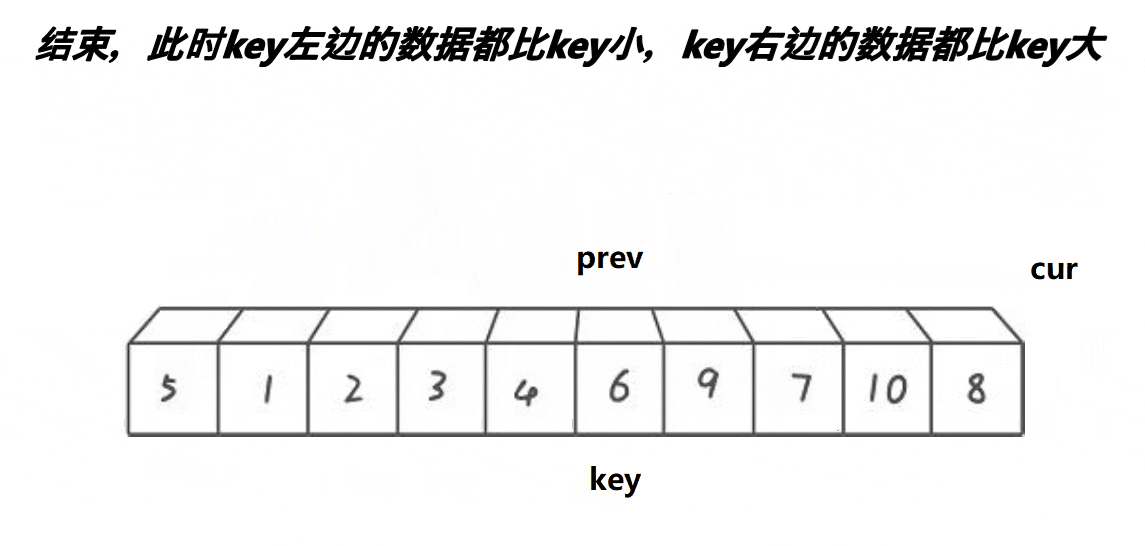
快速排序最初由霍尔（Hoare）提出，其算法逻辑相对复杂。为便于理解，后来发展出了前后指针法实现快排。以下是详细说明：

注：本文提到的"指针"并非真正意义上的指针，而是数组的索引下标

关键概念说明：

key [基准值]

prev [慢指针]

cur [快指针]

  1. 首先选择最左侧元素作为基准值 key ，初始化 prev 指针与 key 同位置，cur 指针指向下一个位置
  2. 当 cur 指向的元素小于 key 时，移动 prev 指针并与 cur 进行元素交换（可以避免原地互换）
  3. cur 指针持续移动，遇到比基准值小的元素时暂停，此时移动 prev 指针并进行交换（非原地交换会将较小元素移至 prev 位置）
  4. 重复上述过程直到 cur 指针越界
  5. 最后交换 key 与 prev 指向的元素，确保基准值左侧元素均小于它，右侧元素均大于它
cpp 复制代码 
//双指针法快排
int ptrSort(int* a, int left, int right)
{
	int keyi = left;
	int prev = left, cur = left + 1;
	while (cur <= right)
	{
		if (a[cur] < a[keyi])
		{
			prev++;
			if (a[cur] != a[prev])
			{
				Swap(&a[cur], &a[prev]);
			}
		}
		cur++;
	}
	Swap(&a[keyi], &a[prev]);
	return prev;
}

至此完成对基准值的排序，之后只需递归地对左右两个子区间执行相同操作（一般使用递归），即可完成整个数组的排序。

2. 双指针移动零

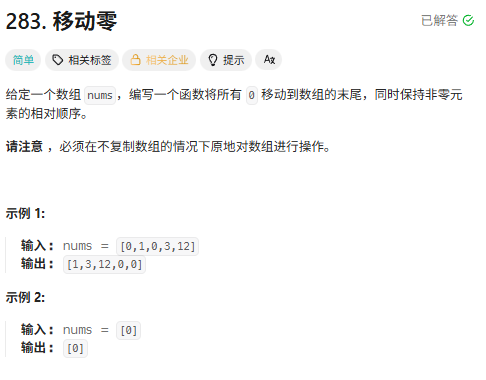
移动零问题可以类比为以零为基准的单次快速排序：

  1. 初始化两个指针：cur指向数组首元素，prev初始化为-1
  2. 遍历过程中：
    • 当cur遇到非零元素时，prev右移一位并与cur交换元素
    • 否则cur继续右移
  3. 重复上述过程直至cur到达数组末尾
cpp 复制代码 
class Solution {
public:
    void moveZeroes(vector<int>& nums) {
        for(int cur = 0,dest = -1;cur<nums.size();cur++)
            if(nums[cur])
                swap(nums[++dest],nums[cur]);
    }
};

3. 复写零

处理复写零问题的关键在于确定结束位置。以下是优化后的双指针解决方案：

  1. 初始化指针：将cur和dest都指向数组首元素，然后cur开始移动
  2. 遍历规则：
    • 当cur指向0时：dest移动两步
    • 当cur指向非零元素时：dest移动一步
  3. 终止条件：当dest到达数组末尾时停止
  4. 边界处理：
    • 若cur指向最后一个元素为0时，dest可能越界
    • 此时需要将dest回退两位，并将末尾元素置零，同时cur回退一位
  5. 逆向复写：由于已精确计算复写元素数量，无需担心原地复写导致的覆盖问题
cpp 复制代码 
class Solution {
public:
    void duplicateZeros(vector<int>& arr) {
        //双指针找最后一个复写的数
       int cur = 0,dest = -1,n = arr.size();
       while(1)
       {
        if(arr[cur] == 0)
            dest++;
        dest++;
        if(dest >= n-1)
            break;//找到退出
        cur++;
       }
       //处理特殊情况
       if(dest == arr.size())
       {
        cur--;
        dest -= 2;
        arr[arr.size()-1] = 0;
       }
       //从后向前复写
       while(cur >= 0)
       {
        if(arr[cur] == 0)
            arr[dest--] = arr[cur];
        arr[dest--] = arr[cur];
        cur--;
       }
    }
};

三、首尾双指针

0. 算法思想:

首尾分别设定指针，可以交换元素解决移动零类似问题；也可以利用单调性解决其他问题

1. 双指针移动零

  • 题目：leetcode:移动零

    如果不需要保持元素的先后顺序的话，也可以使用首尾双指针法
  1. 设置左右指针，left 和 right
  2. left 找0，right 找非零元素，交换
  3. 直到左右指针相遇
cpp 复制代码 
class Solution {
public:
    void moveZeroes(vector<int>& nums) {
        int left = 0,right = nums.size()-1;
        while(left < right)
        {
            if(nums[left]) left++;
            if(nums[right] == 0) right--;
            if(left < right && nums[left] == 0 && nums[right] != 0) swap(nums[left],nums[right]);
        }
    }
};

2. 盛水最多的容器

  • 题目：leetcode：盛水最多的容器
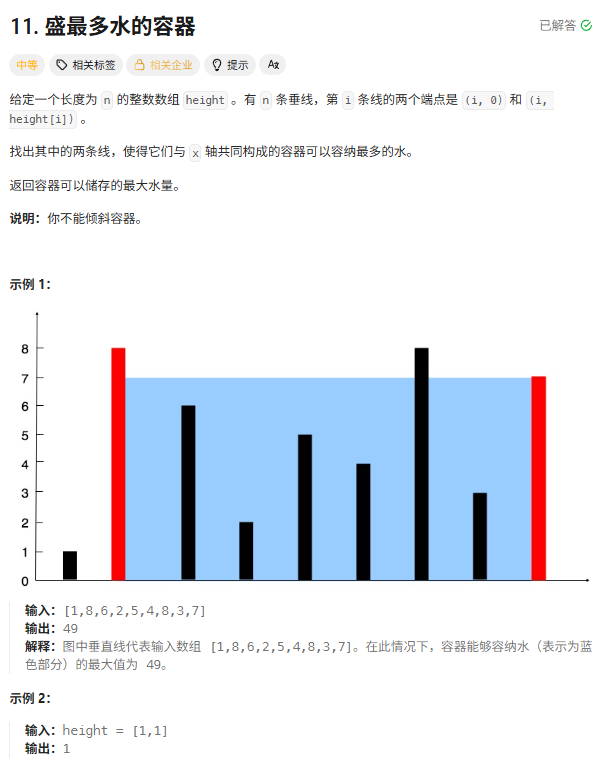
  • 解法一：
    本题可以使用暴力解法来计算，即两层循环计算出 "体积" ， 取其最大值。
  • 解法二：
    根据体积的计算公式 v = w * h ：
  1. 先排序，得到一个有顺序的数组
  2. 首尾设定指针，向内移动，宽度w必定减小，高度由于取最小值，会降低或者不变
  3. 则说明：计算出体积v以后，将二者高度较小的一方排除，向内移动，即可减少遍历次数
cpp 复制代码 
class Solution {
public:

    int getv(vector<int>& height, int left,int right)
    {
        int width = right - left;
        int high = height[right];//假设法
        if(height[left] < height[right])
        {
            high = height[left];
        }
        return width * high;
    }
    int maxArea(vector<int>& height) 
    {
        int left = 0;
        int right = height.size() - 1;
        int v = 0;
        while(left < right)
        {
            int vv = getv(height, left, right);
            if(height[left] < height[right]) left++;
            else right--;
            if(vv > v) v = vv;
        }
        return v;
    }
};

3. 两数之和

  • 题目：两数之和

  • 解法一：

    双层循环，暴力枚举出所有可能值，找到两数之和为目标的两个数。

  • 解法二：

  1. 先排序，依旧设定首位指针
  2. 于是存在：
    • 如果两指针所指元素之和小于目标值:变小一定得不到目标值，所以右指针不能左移，左指针右移
    • 如果两指针所指元素之和大于目标值:变大一定得不到目标值，所以左指针不能右移，右指针左移
  3. 遍历直到找到和为目标值的两个数
cpp 复制代码 
class Solution {
public:
    vector<int> twoSum(vector<int>& price, int target) 
    {
        int left = 0, right = price.size() - 1;
        while(left < right)
        {
            if(price[left] + price[right] > target) 
                right--;
            else if(price[left] + price[right] < target)
                left++;
            else 
                return vector<int>({price[left],price[right]});
        }
        return vector<int>();
    }
};

4. 三数之和

三数之和实际上是两数之和的变式：

解法一：

  • 与两数之和相同，三层循环可以枚举出想要结果，找到以后加入数组即可
    解法二：
  1. 依旧可以先排序，然后固定首尾其中一个数字，依次顺序固定，重复元素跳过
  2. 用两数之和类似双指针法，计算出三数之和为结果的数字，需要注意的是，重复元素跳过
  3. 最后遍历完成，结果加入二维数组
cpp 复制代码 
class Solution {
public:
    vector<vector<int>> threeSum(vector<int>& nums) {
        //优化
        sort(nums.begin(),nums.end());
        int n = nums.size();
        //利用单调性，定尾部，前面走双指针
        vector<vector<int>> vv; 
        for(int i = n-1;i >= 2;i--)
        {
            if ( i < n-1 && nums[i] == nums[i + 1])
            {
                continue;
            }
            int left = 0,right = i-1;
            while(left < right)
            {
                if(nums[left] + nums[right] + nums[i] > 0) right--;
                else if(nums[left] + nums[right] + nums[i] < 0) left ++;
                else 
                {                                            
                    // 找到符合条件的三元组，加入结果
                    vv.push_back({nums[left], nums[right], nums[i]});
                    
                    // 跳过左指针重复值
                    while (left < right && nums[left] == nums[left + 1]) ++left;
                    // 跳过右指针重复值
                    while (left < right && nums[right] == nums[right - 1]) --right;
                    
                    // 双指针收缩，继续找下一组
                    ++left;
                    --right;
                }
            }  
        }   
        return vv;
    }
};

5. 有效三角形的个数

实际上本题也算是三数之和的变式，只不过本体要求三数组成三角形而不是和为零：

解法一：三层循环遍历枚举

解法二：

  1. 先排序，依旧固定一边
  2. 利用三角形两小边之和大于第三边性质寻找三个符合要求的边，符合要求则计入次数
cpp 复制代码 
class Solution {
public:
    int triangleNumber(vector<int>& nums) {
        int n = nums.size()-1;
        sort(nums.begin(),nums.end());
        int sum = 0;
        for(int i = n; i>0; i--)
        {
            int left = 0,right = i-1;
            while(left < right)
            {
                if(nums[left] + nums[right] > nums[i])
                {
                    sum += right-left;
                    right--;
                }
                else
                    left++;
            }
        }
        return sum;
    }
};

6. 四数之和

  • 题目：四数之和

    这里不再讲解原理，原理与三数之和类似，直接看代码：
  • 提一点：本题需要注意的是样例里面存在超大数，所以需要注意 int 无法承载的问题
cpp 复制代码 
class Solution {
public:
    vector<vector<int>> fourSum(vector<int>& nums, int target) {
        int n = nums.size();
        sort(nums.begin(),nums.end());
        vector<vector<int>> vv;
        for(int j = n - 1; j >= 3;j--)
        {
            if(j < n-1 && nums[j] == nums[j+1]) continue;
            int t = target - nums[j];
            for(int i = j - 1; i >=  2;i--)
            {
                if(i < j-1 && nums[i] == nums[i+1]) continue;
                int left = 0,right = i - 1;
                while(left < right)
                {
                    if((long long)nums[left] + nums[right] + nums[i] < (long long)t) left++;
                    else if ((long long)nums[left] + nums[right] + nums[i] > (long long)t) right--;
                    else
                    {
                        vv.push_back({nums[left], nums[right], nums[i],nums[j]});
                        while(left < right && nums[left] == nums[left + 1]) left++;
                        while(left < right && nums[right] == nums[right - 1]) right--;
                        left++,right--;
                    }
                }   
            }
        }
        return vv;
    }
};

三、快慢双指针解决环形问题

0. 算法思想：

用跑圈的问题来类比，如果一个快的人和慢的人在环形跑道跑步，如果他们一直是恒速前进，那么必定相遇，快慢双指针也类似这个问题

1. 环形链表

程序员遇到的经典环形问题是：leetcode：环形链表问题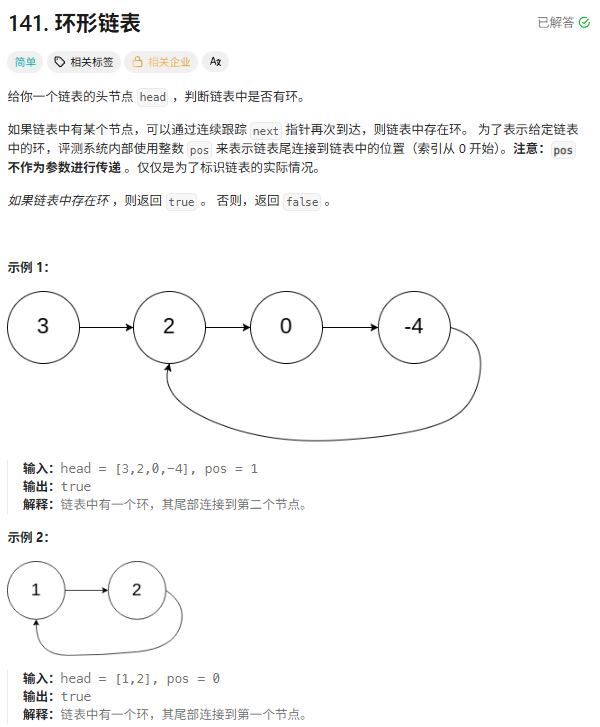

采用快慢指针的思想，如果有环就必定能相遇，而如果没环必定能越界

cpp 复制代码 
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    bool hasCycle(ListNode *head) {
        typedef struct ListNode ListNode;
        ListNode* fast = head;
        ListNode* slow = head;
        while(fast!=NULL && fast->next!= NULL)
        {
            fast = fast->next->next;
            slow = slow->next;
            if(slow == fast)
            {
                return true;
            }
        }
        return false;
    }
};

2. 快乐数

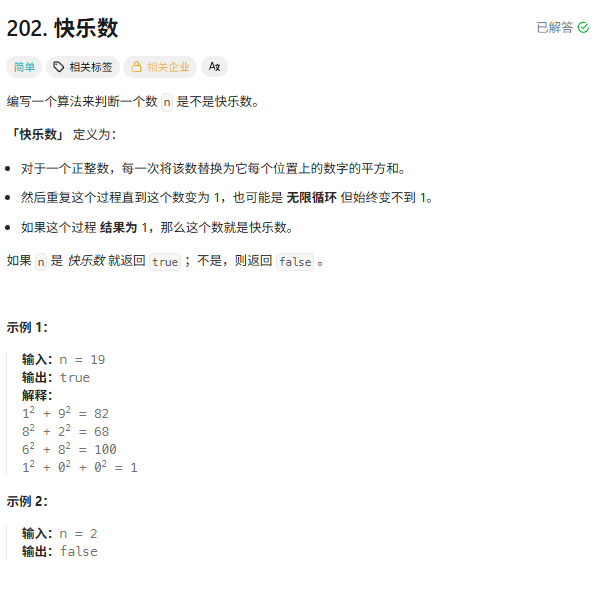
本题的两种情况其实可以看作是一种情况：

  • 有环：环内无1，成一个大环
  • 有环：环内只有1，可看作一循环，即为快乐数
    所以只需要判断快慢指针相遇的时候他们所指元素的值是不是1，即可判断是否是快乐数
cpp 复制代码 
class Solution {
public:

    int get_sosq(int& n)//获取平方和
    {
        int sum = 0;
        while (n)
        {
            sum += pow((n % 10), 2);
            n /= 10;
        }
        return sum;
    }
    bool isHappy(int n) {
        int show = n, fast = n;
        show = get_sosq(show);
        fast = get_sosq(fast);
        fast = get_sosq(fast);
        while (show != fast)
        {
            show = get_sosq(show);
            fast = get_sosq(fast);
            fast = get_sosq(fast);
        }
        if (fast == 1)
            return true;
        return false;
    }
};
  • 本节完...
相关推荐
追随者永远是胜利者1 小时前
（LeetCode-Hot100）33. 搜索旋转排序数组
java·算法·leetcode·职场和发展·go
你怎么知道我是队长1 小时前
计算机系统基础3---值的表示2---定点数与浮点数的介绍
算法
云深处@2 小时前
【数据结构】栈
数据结构·算法
啊我不会诶2 小时前
Codeforces Round 1076 (Div. 3) vp补题
算法·深度优先
Bear on Toilet2 小时前
递归_二叉树_49 . 路径综合Ⅲ
数据结构·算法·前缀和·深度优先·递归
CHANG_THE_WORLD2 小时前
深入指针3 - 完全精讲版
数据结构·算法
im_AMBER2 小时前
Leetcode 124 二叉搜索树的最小绝对差 | 二叉树的锯齿形层序遍历
数据结构·学习·算法·leetcode·二叉树
ADDDDDD_Trouvaille2 小时前
2026.2.14——OJ78-82题
c++·算法
Hag_202 小时前
LeetCode Hot100 560.和为K的子数组
数据结构·算法·leetcode
热门推荐
01从零搭建一个 PHP 登录注册系统（含完整源码）02使用 1panel面板 部署 php网站03GitHub 镜像站点04AI Agent 平台横评：ZeroClaw vs OpenClaw vs Nanobot05MIUI显示/隐藏5G开关的方法，信号弱时开启手机Wifi通话方法06PHP Error: 常见错误及其解决方法07Claude Code + GLM4.7 避坑指南：解决 Unable to connect to Anthropic services08openClaw安装飞书插件｜核心踩坑：spawn EINVAL 错误终极解决指南09如何将 TRAE IDE 的插件市场源切换至 VS Code 官方市场10全面体验 Grok API 中转站（2025 · Grok 4 系列最新版）