647. 回文子串 - 力扣(LeetCode)
前提:
回文字符串 是正着读和倒过来读一样的字符串。
子字符串 是字符串中的由连续字符组成的一个序列。
1、确定dp数组
判断字符串S是否是回文,那么如果我们知道 s[1],s[2],s[3] 这个子串是回文的,那么只需要比较 s[0]和s[4]这两个元素是否相同,如果相同的话,这个字符串s 就是回文串。
2、确定递推公式
s[i]与s[j]判断有两种;
一种是当s[i]与s[j]不相等,那没啥好说的了,dp[i][j]一定是false。
另一种是当s[i]与s[j]相等时,这就复杂一些了,有如下三种情况:
情况一:下标i 与 j相同,同一个字符例如a,当然是回文子串
情况二:下标i 与 j相差为1,例如aa,也是回文子串
情况三:下标:i 与 j相差大于1的时候,例如cabac,此时s[i]与s[j]已经相同了,我们看i到j区间是不是回文子串就看aba是不是回文就可以了,那么aba的区间就是 i+1 与 j-1区间,这个区间是不是回文就看dp[i + 1][j - 1]是否为true。
3、dp数组初始化
dp[i][j]初始化为false;
4、遍历顺序
一定要从下到上,从左到右遍历,这样保证dp[i + 1][j - 1]都是经过计算
5、举例推导dp数组
以输出'aaa'为例,dp[i][j]状态如下:
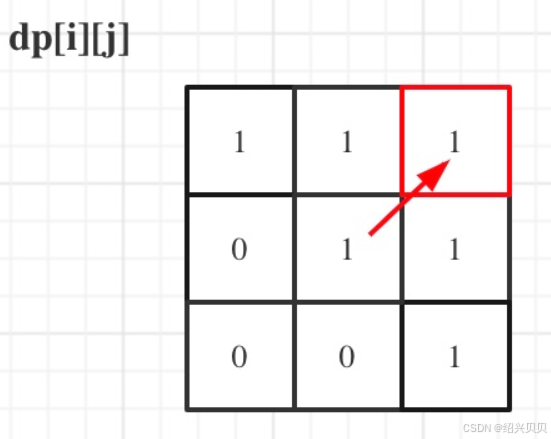
python
class Solution:
def countSubstrings(self, s: str) -> int:
dp = [[False]*len(s) for _ in range(len(s))]
res = 0
# 注意遍历顺序,倒序遍历
for i in range(len(s)-1, -1, -1):
for j in range(i, len(s)):
# 情况一和情况二
if s[i] == s[j]:
if j - i <= 1:
res += 1
dp[i][j] = True
elif dp[i+1][j-1]:
res += 1
dp[i][j] = True
return res
if __name__ == '__main__':
s = "abc"
res = Solution().countSubstrings(s)
print(res)516. 最长回文子序列 - 力扣(LeetCode)
回文子串是要连续的,回文子序列可不是连续的!
1、确定dp数组
dp[i][j]:字符串s在[i, j]范围内最长的回文子序列的长度为dp[i][j]。
2、确定递推公式
判断回文子串的题目中,关键逻辑就是看s[i]与s[j]是否相同;
如果s[i]与s[j]相同,那么dp[i][j] = dp[i + 1][j - 1] + 2;
如果s[i]与s[j]不相同,dp[i][j]一定是取最大的,即:dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);
3、dp数组如何初始化
当i与j相同,那么dp[i][j]一定是等于1;其他情况dp[i][j]初始为0就行。
python
class Solution:
def longestPalindromeSubseq(self, s: str) -> int:
dp = [[0] * len(s) for _ in range(len(s))]
for i in range(len(s)):
dp[i][i] = 1
for i in range(len(s)-1, -1, -1):
for j in range(i+1, len(s)):
if s[i] == s[j]:
dp[i][j] = dp[i+1][j-1] + 2
else:
dp[i][j] = max(dp[i+1][j], dp[i][j-1])
return dp[0][-1]
if __name__ == '__main__':
s = "bbbab"
res = Solution().longestPalindromeSubseq(s)
print(res)动态规划总结
动规五部曲分别为:
- 确定dp数组(dp table)以及下标的含义
- 确定递推公式
- dp数组如何初始化
- 确定遍历顺序
- 举例推导dp数组
要清楚每一个步骤所代表的含义和意义,才能真正明白动态规划的题目,光想递推公式,就算解题了也是稀里糊涂的,没有真正了解全貌;