机器学习与模式识别——机器学习中的搜索算法

一．实验目的

熟悉梯度下降算法和次梯度下降算法的应用。
熟悉随机梯度下降算法的应用。
熟悉牛顿迭代算法的应用。

二．实验内容

1.上机实验题一

实现例4.5 用Lasso回归拟合多项式模型。

2 .上机实验题二

用基于线性回归的随机梯度下降算法来求解房价预测问题。实现书中图4.12。并对比梯度下降算法和随机梯度下降算法的收敛过程，实现图4.14。并作出总结。

3 .上机实验题三

用牛顿迭代算法求解的最小值，给出编程过程

三．实验要求

1.结合上课内容，写出程序，并调试程序，要给出测试数据和实验结果。

2.整理上机步骤，总结经验和体会。

3.完成实验报告和上交源程序

四、运行代码

1 、 上机实验题一

首先定义了一个名为Lasso的类，用于实现Lasso回归，这是一种线性回归的变体，通过引入L1正则化项（即权重的绝对值之和）来促进稀疏解，从而进行特征选择。在Lasso类中，初始化正则化参数Lambda，fit方法用于训练模型，其中X是特征矩阵，y是目标值向量，eta是学习率，N是迭代次数。在训练过程中，模型通过迭代更新权重w来最小化损失函数，其中包括了L1正则化项。predict方法用于根据训练好的模型进行预测。

接着，生成了一组样本数据X和y，其中X是从均匀分布中随机生成的，y是X的线性变换加上一些噪声。然后，使用PolynomialFeatures从sklearn.preprocessing模块来生成多项式特征，以增加模型的复杂性。之后，创建了一个Lasso模型实例，设置了正则化参数Lambda为0.001，并调用fit方法来训练模型，使用多项式特征X_poly和目标值y。

最后，绘制原始数据点和模型预测的曲线。首先，设置坐标轴的范围，然后绘制原始数据点。接着，生成一系列用于绘图的点W，并使用多项式特征转换W_poly，最后使用训练好的模型来预测这些点的值u，并绘制出预测曲线。

（1）定义Lasso回归类

python 复制代码

import numpy as np

class Lasso:
    def __init__(self, Lambda=1):
        self.Lambda = Lambda

    def fit(self, X, y, eta=0.1, N=1000):
        m,n = X.shape
        w = np.zeros((n,1)) 
        self.w = w
        for t in range(N):
            e = X.dot(w) - y
            v = 2 * X.T.dot(e) / m + self.Lambda * np.sign(w)
            w = w - eta * v  
            self.w += w
        self.w /= N
        return 
    
    def predict(self, X):
        return X.dot(self.w)

（2）用Lasso回归拟合多项式模型

python 复制代码

import numpy as np
from sklearn.preprocessing import PolynomialFeatures
from search_algorithms.lib.lasso import Lasso
import matplotlib.pyplot as plt

def generate_samples(m):
    X = 2 * (np.random.rand(m, 1) - 0.5) 
    y = X + np.random.normal(0, 0.3, (m,1))
    return X, y

np.random.seed(100)
X, y = generate_samples(10)
poly = PolynomialFeatures(degree = 10)
X_poly = poly.fit_transform(X)
model = Lasso(Lambda=0.001)
model.fit(X_poly, y, eta=0.01, N=50000)

plt.axis([-1, 1, -2, 2])
plt.scatter(X, y)
W = np.linspace(-1, 1, 100).reshape(100, 1)
W_poly = poly.fit_transform(W)
u = model.predict(W_poly)
plt.plot(W, u)
plt.show()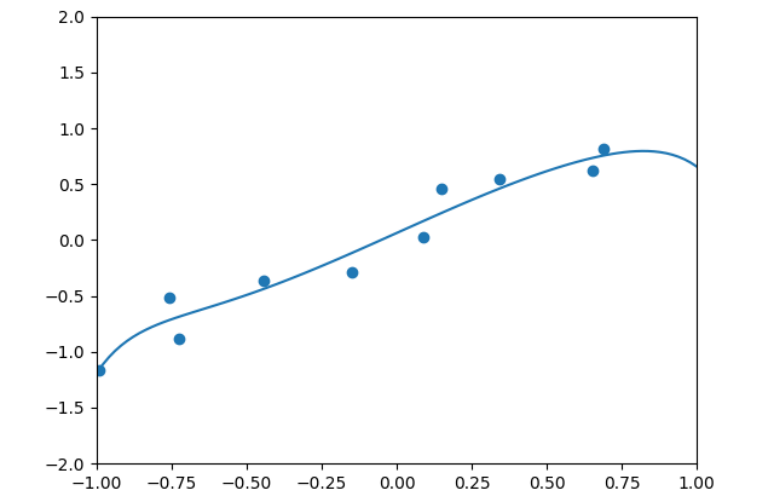

2 、 上机实验题 二

首先，定义了一个梯度下降的LinearRegression类，该类使用梯度下降算法来训练模型。fit方法接受输入数据X和目标值y，以及学习率eta和迭代次数N。在每次迭代中，算法计算预测值和实际值之间的误差，然后更新权重w以最小化误差。权重更新过程重复N次，并且每次迭代的权重都被记录在weights_history中。predict方法使用训练好的权重来预测新的输入数据。接着，定义了一个随机梯度下降的LinearRegression类，但这次使用的是随机梯度下降算法。fit方法的参数与梯度下降版本相似，但增加了eta_0和eta_1用于调整学习率。在每次迭代中，算法随机选择一个样本来计算误差和梯度，并更新权重。权重更新同样记录在weights_history中。

最后进行梯度下降算法和随机梯度下降算法的比较，它首先生成一个模拟的回归数据集。然后，它分别使用梯度下降和随机梯度下降算法来训练两个线性回归模型。在训练过程中，它收集了每次迭代的权重，并打印出最终的权重值。

（1）梯度下降算法

python 复制代码

import numpy as np
    
class LinearRegression: 
    def fit(self, X, y, eta, N):
        m, n = X.shape
        w = np.zeros((n,1))
        for t in range(N):
            e = X.dot(w) - y
            g = 2 * X.T.dot(e) / m
            w = w - eta * g
        self.w = w
    
    def predict(self, X):
        return X.dot(self.w)

（2）随机梯度下降算法

python 复制代码

import numpy as np
    
class LinearRegression:    
    def fit(self, X, y, eta_0=10, eta_1=50, N=3000):
        m, n = X.shape
        w = np.zeros((n,1))
        self.w = w
        for t in range(N):
            i = np.random.randint(m)
            x = X[i].reshape(1,-1)
            e = x.dot(w) - y[i]
            g = 2 * e * x.T
            w = w - eta_0 * g / (t + eta_1) 
            self.w += w
        self.w /= N
    
    def predict(self, X):
        return X.dot(self.w)

（3）梯度下降算法VS随机梯度下降算法

python 复制代码

import numpy as np
from sklearn.datasets import make_regression
import lib.linear_regression_gd as gd
import lib.linear_regression_sgd as sgd
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['SimSun']
plt.rcParams['axes.unicode_minus']=False
# 生成数据集
X, y = make_regression(n_samples=100, n_features=2, noise=0.1, bias=0, random_state=0)
y = y.reshape(-1, 1)

# 梯度下降模型
model_gd = gd.LinearRegression()
weights_gd = model_gd.fit(X, y, eta=0.01, N=3000)
print(model_gd.w)

# 随机梯度下降模型
model_sgd = sgd.LinearRegression()
weights_sgd = model_sgd.fit(X, y, eta_0=10, eta_1=50, N=3000)
print(model_sgd.w)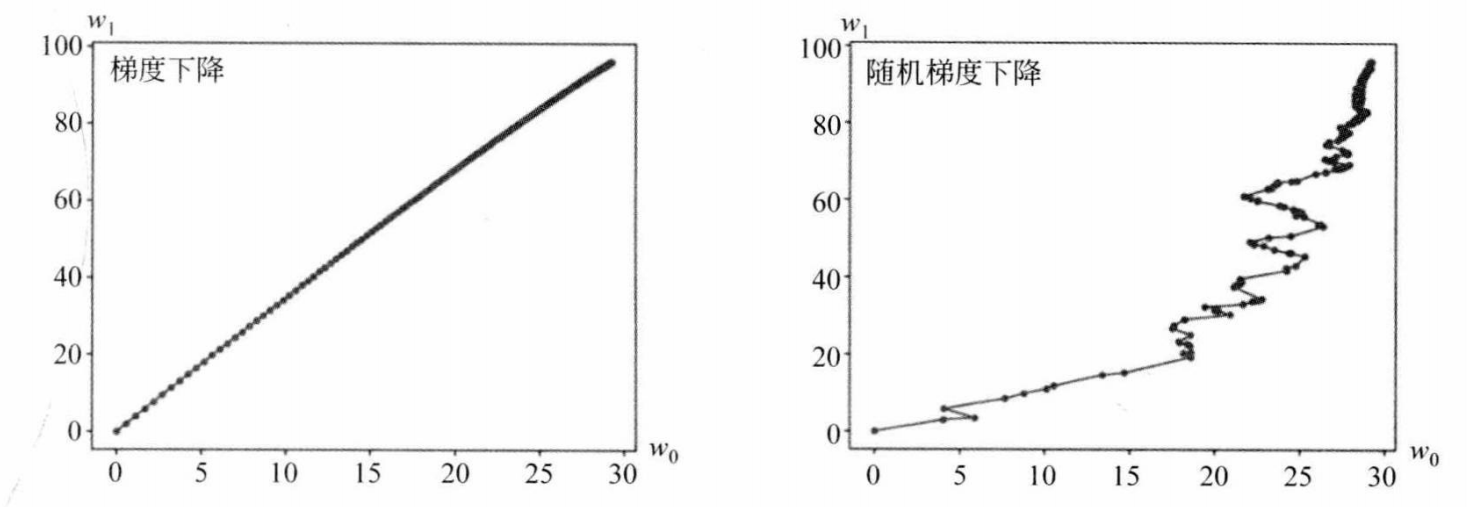

3 、 上机实验题 三

首先，定义了一个符号变量x，然后定义了目标函数f`。接着，定义了两个函数get_grad和get_hess分别用于计算函数的一阶导数和二阶导数，并将这些导数在给定的x_val处求值。

牛顿迭代法的核心是newton_iter函数，它接受一个初始点x0和一个误差阈值err作为输入。在迭代过程中，每次循环都会计算当前点的一阶导数和二阶导数，然后使用牛顿迭代公式更新x0的值。迭代继续进行，直到一阶导数的绝对值小于或等于误差阈值err`，这表明已经找到了函数的最小值点。在每次迭代中，都会打印出当前的迭代次数和x的值，以便跟踪迭代过程。当迭代结束时，会打印出总的迭代次数和最终的x值，这个值就是函数的最小值点。最后，代码设置了初始点x0为1和误差阈值err为，然后调用newton_iter函数开始迭代过程。

python 复制代码

from sympy import *

# 定义符号
x = symbols('x')
# 定义所求函数
f = x ** 2 - x + 1
# 求解导数值
def get_grad(f, x_val):
    # 计算一阶导数
    f_prime = diff(f, x)
    # 代入具体数值计算
    grad = f_prime.subs(x, x_val)
    return grad

# 求解二阶导数值
def get_hess(f, x_val):
    # 计算二阶导数
    f_double_prime = diff(f, x, 2)
    # 代入具体数值计算
    hess = f_double_prime.subs(x, x_val)
    return hess

# 牛顿迭代
def newton_iter(x0, err):
    # 记录迭代次数
    count = 0
    while True:
        # 得到导数值
        grad = get_grad(f, x0)
        # 得到二阶导数值
        hess = get_hess(f, x0)
        # 检查是否收敛
        if abs(grad) <= err:
            break
        else:
            # 迭代公式
            x1 = x0 - grad / hess
            count += 1
            print('第', count, '次迭代: x =', x1)
            x0 = x1  # 更新x0为新的迭代值
    print('迭代次数为:', count)
    print('迭代结果为', x0)

# 设置初始点
x0 = 1
err = 1e-10
newton_iter(x0, err)