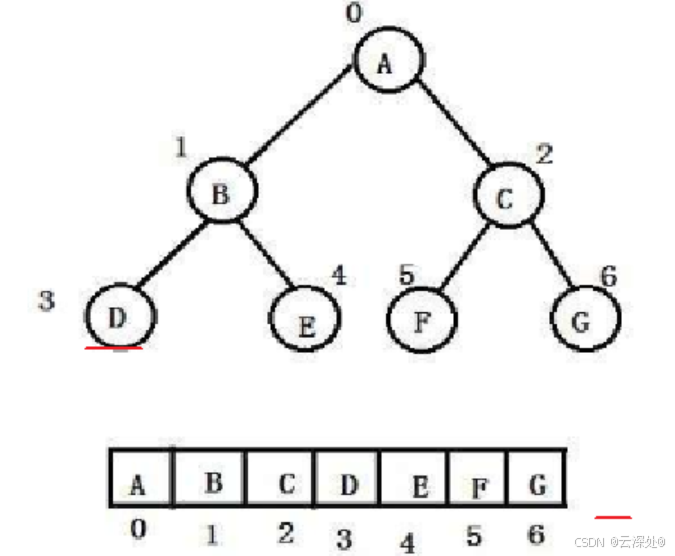
树概念及结构
树的概念
- 树是一种非线性的数据结构,它是由n(n>=0)个有限结点组成一个具有层次关系的集合。
- 除根结点外,其余结点被分成M(M>0)个互不相交的集合T1、T2、......、Tm,其中每一个集合Ti(1<= i <= m)又是一棵结构与树类似的子树。每棵子树的根结点有且只有一个前驱,可以有0个或多个后继
因此,树是递归定义的。
注意:树形结构中,子树之间不能有交集,否则就不是树形结构
树的相关概念
- 结点的度:一个结点含有的子树的个数称为该结点的度;
- 叶结点或终端结点:度为0的结点称为叶结点;
- 非终端结点或分支结点:度不为0的结点;
- 双亲结点或父结点:若一个结点含有子结点,则这个结点称为其子结点的父结点;
- 孩子结点或子结点:一个结点含有的子树的根结点称为该结点的子结点;
- 兄弟结点:具有相同父结点的结点互称为兄弟结点;
- 树的度:一棵树中,最大的结点的度称为树的度;
- 结点的层次:从根开始定义起,根为第1层,根的子结点为第2层,以此类推;
- 树的高度或深度:树中结点的最大层次;
- 森林:由m(m>0)棵互不相交的树的集合称为森林;
二叉树的基本概念与定义
概念
- 每个节点最多有两个子节点的特性
- 常见术语解释:根节点、叶子节点、子树、深度、高度等。
二叉树的常见类型
满二叉树,完全二叉树
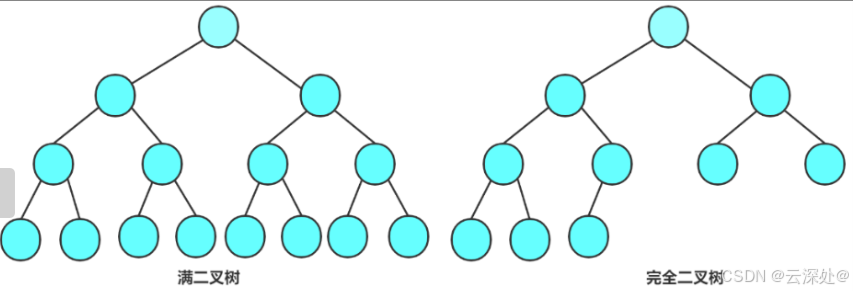
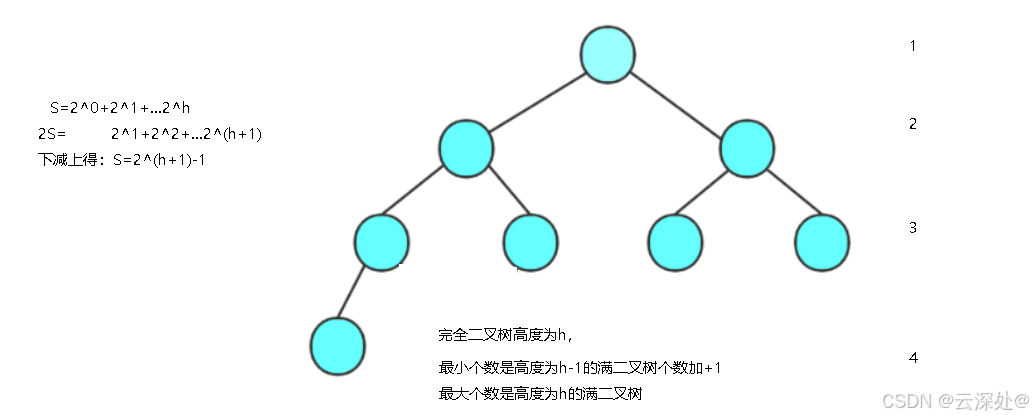
满二叉树是一个父节点都有两个子节点,高度为h,最下面一层为叶子节点,数量为2^h-1
完全二叉树不全满,节点数量[2^(h-1),2^h-1]
二叉树的存储方式
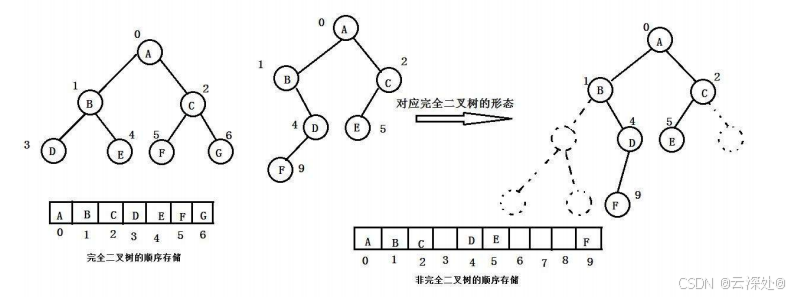
顺序存储(数组表示)
- 顺序结构存储就是使用数组来存储,一般使用数组只适合表示完全二叉树,所以完全二叉树会有空间的浪费。
- 而现实中使用中只有堆才会使用数组来存储
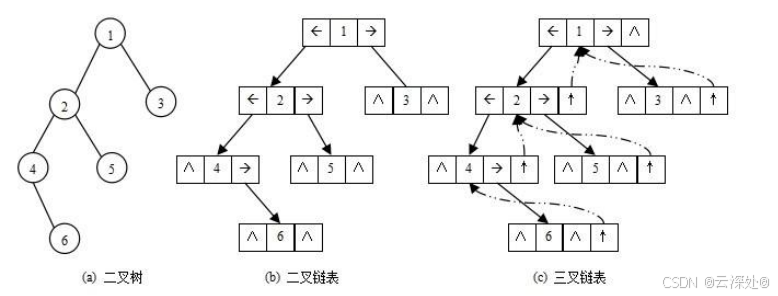
与链式存储(节点结构体/类)
- 二叉树的链式存储结构是指,用链表来表示一棵二叉树,即用链来指示元素的逻辑关系。
- 通常的方法是链表中每个结点由三个域组成,数据域和左右指针域,左右指针分别用来给出该结点左孩子和右孩子所在的链结点的存储地址 。
- 链式结构又分为二叉链和三叉链,红黑树等会用到三叉链。
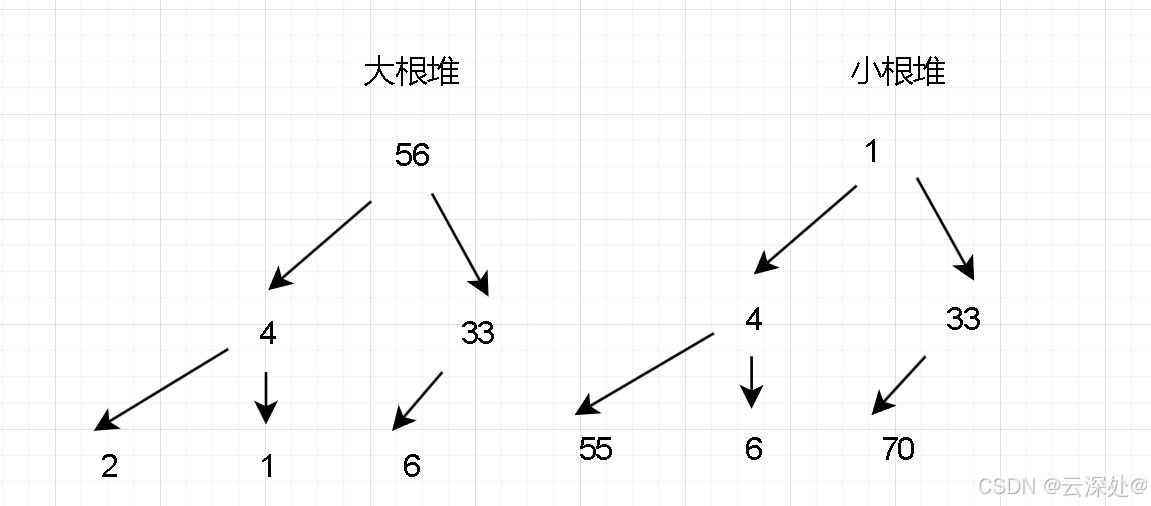
堆(一种二叉树)
堆的概念
- 已知一个集合里的元素,将其按照完全二叉树的格式储存起来,其中根节点最大的堆为大根堆,根节点最小的堆为小根堆。
- 所有元素按完全二叉树的顺序储存在一维数组中
- 堆中的某个节点总是不大于或者不小于父节点的值
小根堆&&大根堆
逻辑结构&&物理结构
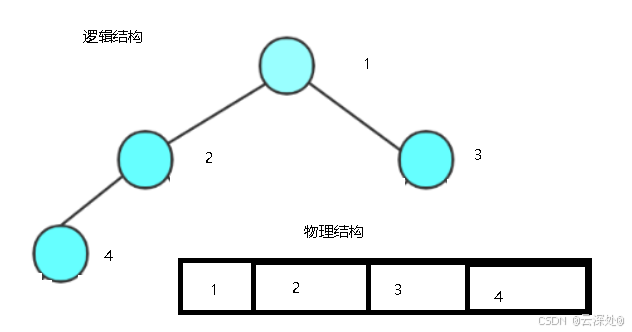
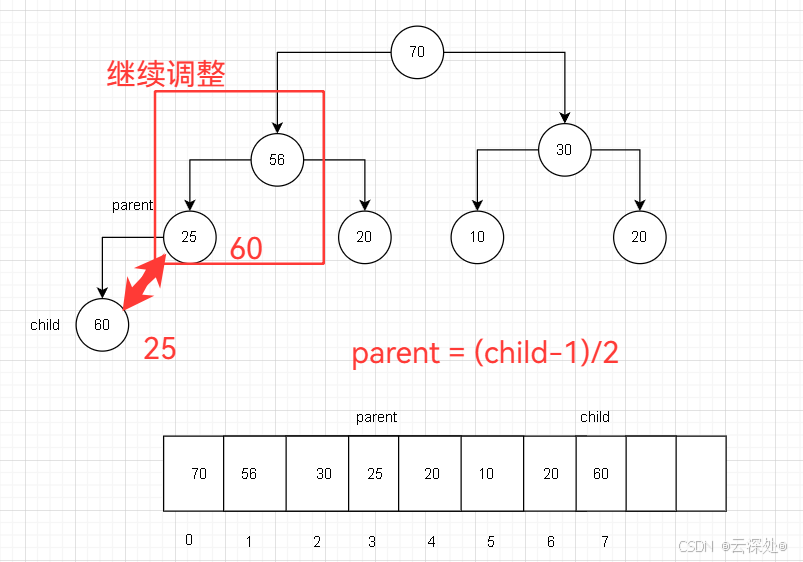
二叉树的值在数组位置中父子下标关系:
- parent=(child-1)/2
- leftchild=parent*2+1
- rightchild=parent*2+2
堆的实现
-
堆的核心价值在于快速获取和删除极值(堆顶元素)(比如大顶堆的最大值、小顶堆的最小值),这也是堆被用于优先队列、堆排序的核心原因
-
因此插入时向上调整,删除时向下调整。都使用交换元素的方式,重新达到大堆或小堆
结构体定义
底层是数组,所以用size和capacity来判断扩容逻辑
cpp
typedef int HpData;
typedef struct Heap
{
HpData* a;
int size;
int capacity;
}Hp;初始化和删除
cpp
void HpInit(Hp* hp)
{
assert(hp);
hp->a = NULL;
hp->size = hp->capacity = 0;
}
void HpDel(Hp* hp)
{
assert(hp);
free(hp->a);
hp->a = NULL;
hp->size = hp->capacity = 0;
}
void Swap(HpData* p1, HpData* p2)
{
HpData tmp = *p1;
*p1 = *p2;
*p2 = tmp;
}插入数据
- 实现了扩容逻辑
- 向上调整
cpp
void HpPush(Hp* hp, HpData x)
{
assert(hp);
if (hp->capacity == hp->size)
{
int newcapacity = hp->capacity == 0 ? 4 : hp->capacity * 2;
HpData* tmp = (HpData*)realloc(hp->a, sizeof(HpData) * newcapacity);
if (tmp == NULL)
{
perror("realloc fail");
return;
}
hp->a = tmp;
hp->capacity = newcapacity;
}
hp->a[hp->size++] = x;
AdUp(hp->a, hp->size - 1);
}向上调整
- 每插入一个数据都要向上调整,这里实现的大堆
- 当在数组最后插入数据时,这个元素的下标已知,根据前面的parent=(child-1)/2得到parent的下标
- 将数组里面parent下标和child下标的值进行比较,如果a[child]>a[parent],则交换两个元素
- 之后child=parent,parent继续向上
- 循环结束的条件是!(child>0)
cpp
void AdUp(HpData* a, int child)
{
int parent = (child - 1) / 2;
while (child > 0)
{
if (a[child] > a[parent])
{
Swap(&a[child], &a[parent]);
child = parent;
parent = (child - 1) / 2;
}
else break;
}
}删除
- 交换起始元素和最后元素,此时第一个元素为小,其他部分是正常的大堆
- 向下排序,从parent开始
cpp
void HpPop(Hp* hp)
{
assert(hp);
assert(!HpEmpty(hp));
Swap(&hp->a[--hp->size], &hp->a[0]);
AdDown(hp->a, 0, hp->size);
}向下调整
先假设左孩子小,通过比较找到最大的孩子,交换parent和child
避免越界访问,先判断child+1 < n
parent=child,child=(parent+1)/2
结束条件:child>=n
cpp
void AdDown(HpData* a, int parent, int n)
{
int child = (parent + 1) / 2;
while (child < n)
{
if (child+1 < n && a[child] < a[child + 1])
{
child++;
}
Swap(&a[parent], &a[child]);
parent = child;
child = (parent + 1) / 2;
}
}其余逻辑
cpp
bool HpEmpty(Hp* hp)
{
return hp->size == 0;
}
void HpPop(Hp* hp)
{
assert(hp);
assert(!HpEmpty(hp));
Swap(&hp->a[--hp->size], &hp->a[0]);
AdDown(hp->a, 0, hp->size);
}
HpData HpTop(Hp* hp)
{
assert(hp);
assert(!HpEmpty(hp));
return hp->a[0];
}