- 计算布尔二叉树的值
- 求根节点到叶节点数字之和
- 二叉树剪枝
- 验证二叉搜索树
- [二叉搜索树中第 K 小的元素](#二叉搜索树中第 K 小的元素)
- 二叉树的所有路径
我们这次来解决一些二叉数类型的深度优先搜索。
计算布尔二叉树的值
题目描述
给你一棵 完整二叉树 的根,这棵树有以下特征:
叶子节点 要么值为 0 要么值为 1 ,其中 0 表示 False ,1 表示 True 。
非叶子节点 要么值为 2 要么值为 3 ,其中 2 表示逻辑或 OR ,3 表示逻辑与 AND 。
计算 一个节点的值方式如下:
如果节点是个叶子节点,那么节点的 值 为它本身,即 True 或者 False 。
否则,计算 两个孩子的节点值,然后将该节点的运算符对两个孩子值进行 运算 。
返回根节点 root 的布尔运算值。
完整二叉树 是每个节点有 0 个或者 2 个孩子的二叉树。
叶子节点 是没有孩子的节点。
示例 1:
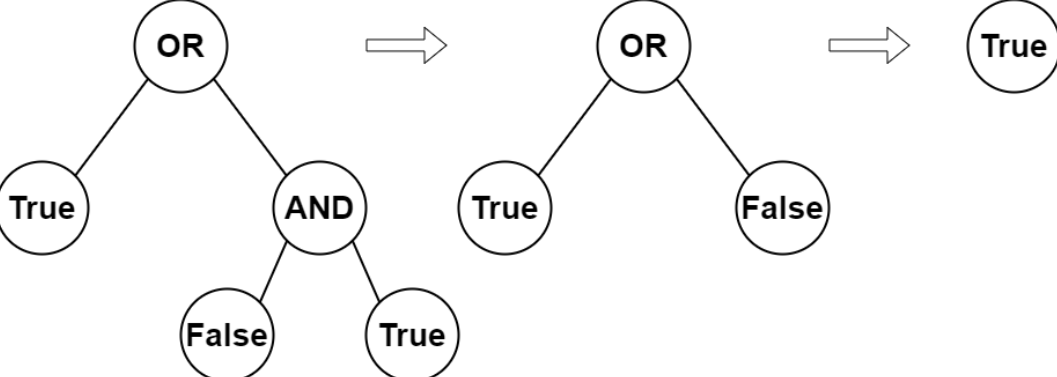
输入:root = [2,1,3,null,null,0,1]
输出:true
解释:上图展示了计算过程。
AND 与运算节点的值为 False AND True = False 。
OR 运算节点的值为 True OR False = True 。
根节点的值为 True ,所以我们返回 true 。
示例 2:
输入:root = [0]
输出:false
解释:根节点是叶子节点,且值为 false,所以我们返回 false 。
提示:
- 树中节点数目在 [1, 1000] 之间。
- 0 <= Node.val <= 3
- 每个节点的孩子数为 0 或 2 。
- 叶子节点的值为 0 或 1 。
- 非叶子节点的值为 2 或 3 。
算法原理和实现
根据题目描述和我们递归缩减规模的思想。
如果是叶子结点直接返回,否则返回左右子树的或/与:
cpp
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
bool evaluateTree(TreeNode* root) {
if(root->val<=1)return root->val;
else if(root->val==2)return evaluateTree(root->left)||evaluateTree(root->right);
else return evaluateTree(root->left)&&evaluateTree(root->right);
}
};求根节点到叶节点数字之和
题目描述
给你一个二叉树的根节点 root ,树中每个节点都存放有一个 0 到 9 之间的数字。
每条从根节点到叶节点的路径都代表一个数字:
例如,从根节点到叶节点的路径 1 -> 2 -> 3 表示数字 123 。
计算从根节点到叶节点生成的 所有数字之和 。
叶节点 是指没有子节点的节点。
示例 1:
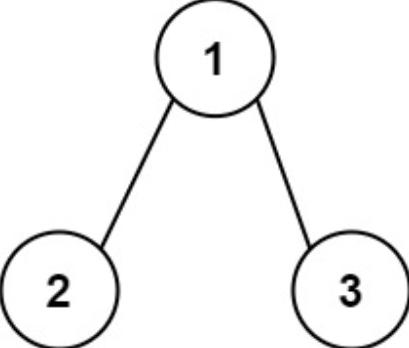
输入:root = [1,2,3]
输出:25
解释:
从根到叶子节点路径 1->2 代表数字 12
从根到叶子节点路径 1->3 代表数字 13
因此,数字总和 = 12 + 13 = 25
示例 2:
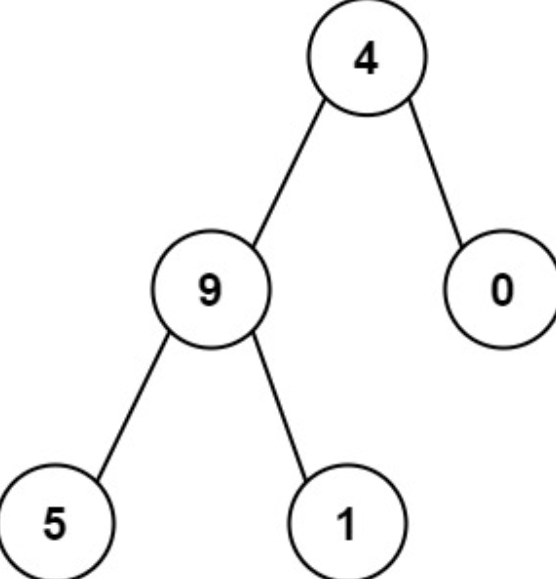
输入:root = [4,9,0,5,1]
输出:1026
解释:
从根到叶子节点路径 4->9->5 代表数字 495
从根到叶子节点路径 4->9->1 代表数字 491
从根到叶子节点路径 4->0 代表数字 40
因此,数字总和 = 495 + 491 + 40 = 1026
提示:
- 树中节点的数目在范围 [1, 1000] 内
- 0 <= Node.val <= 9
- 树的深度不超过 10
算法原理和实现
首先根据二叉树的拆解,如果他是叶子结点,那么返回当前结点值,拼接上前缀值即可。
没错我们还需要一个前缀数值:
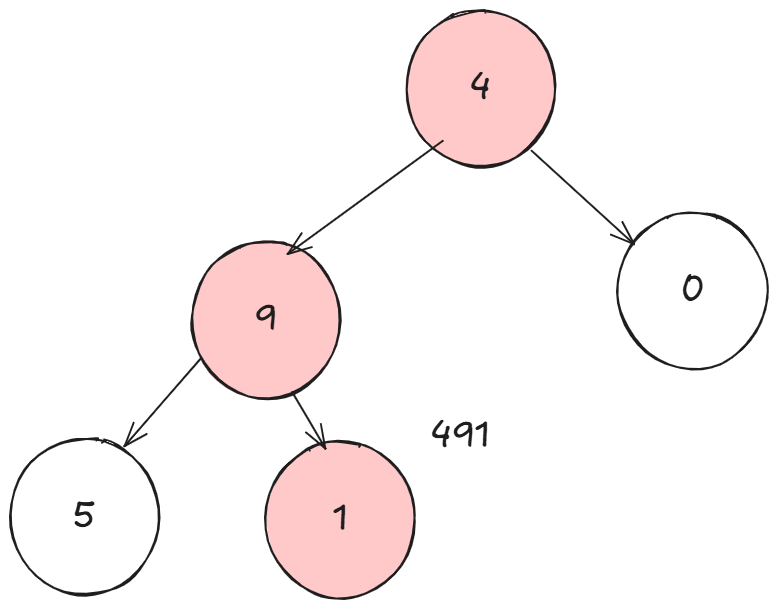
可以看到,这个叶子结点我们理应返回491,这个49该如何来的,自然需要9传递下来:
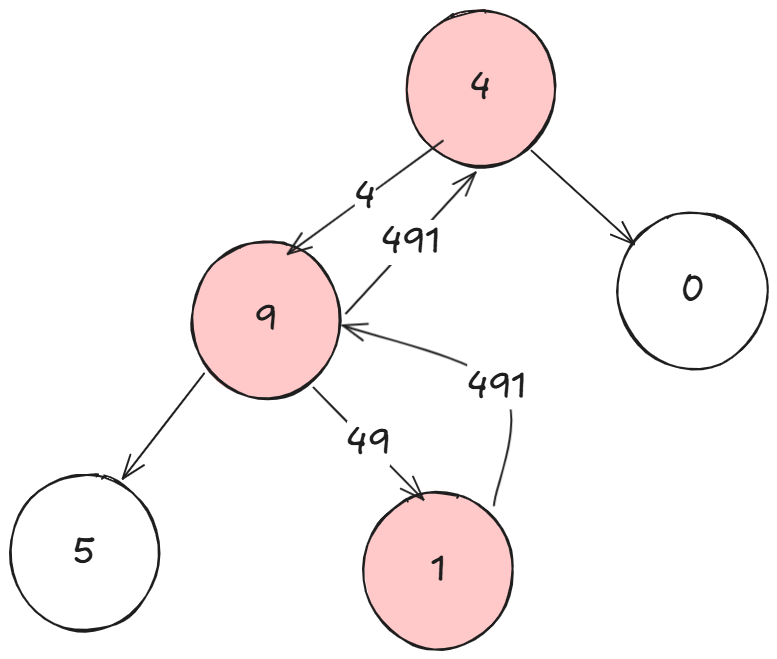
这是叶子结点。如果不是叶子结点,自然就是返回左右结点的路径数字之和。并且我们要将前缀和当前结点的值拼接,并传递下去:
cpp
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int dfs(TreeNode*root,int prev){
if(!root)return 0;
else if(!root->left&&!root->right){
return 10*prev+root->val;
}
else return dfs(root->left,10*prev+root->val)+dfs(root->right,10*prev+root->val);
}
int sumNumbers(TreeNode* root) {
return dfs(root,0);
}
};二叉树剪枝
题目描述
给你二叉树的根结点 root ,此外树的每个结点的值要么是 0 ,要么是 1 。
返回移除了所有不包含 1 的子树的原二叉树。
节点 node 的子树为 node 本身加上所有 node 的后代。
示例 1:

输入:root = [1,null,0,0,1]
输出:[1,null,0,null,1]
解释:
只有红色节点满足条件"所有不包含 1 的子树"。 右图为返回的答案。
示例 2:

输入:root = [1,0,1,0,0,0,1]
输出:[1,null,1,null,1]
示例 3:
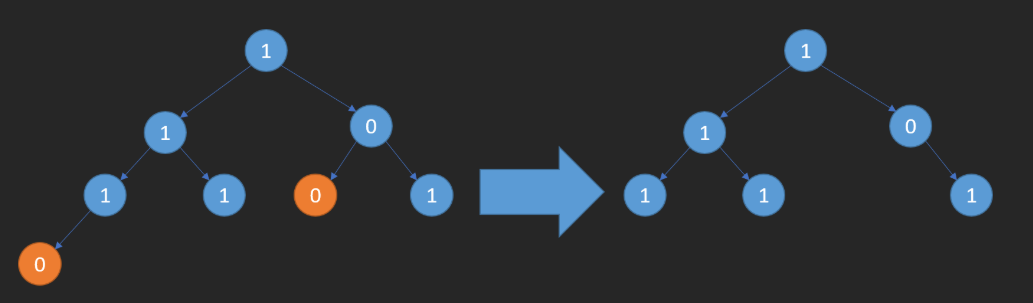
输入:root = [1,1,0,1,1,0,1,0]
输出:[1,1,0,1,1,null,1]
提示:
- 树中节点的数目在范围 [1, 200] 内
- Node.val 为 0 或 1
算法原理和实现
递归实现的思考很简单,我们可以考虑先对左右字树剪枝。剪完后再看看自身需不需要剪掉,如果自身是叶子结点并且是0就需要剪掉:
cpp
class Solution {
public:
TreeNode* pruneTree(TreeNode* root) {
if(root->left)root->left=pruneTree(root->left);
if(root->right)root->right=pruneTree(root->right);
if(!root->left&&!root->right&&!root->val)return nullptr;
return root;
}
};因为我们这里不知道TreeNode是怎么的得到的是栈上还是堆上,是malloc还是new?因此这里不做释放空间处理。
验证二叉搜索树
题目描述
给你一个二叉树的根节点 root ,判断其是否是一个有效的二叉搜索树。
有效 二叉搜索树定义如下:
- 节点的左子树只包含 严格小于 当前节点的数。
- 节点的右子树只包含 严格大于 当前节点的数。
- 所有左子树和右子树自身必须也是二叉搜索树。
递归
首先我们根据定义,判断当前左子树结点是否严格小于当前结点,右子树结点是否严格大于当前结点。
不过这样判断略显麻烦,我们可以将当前结点传给左右子树,让他们自行判断。
随后再判断左右子树是不是二叉搜索树:
cpp
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
bool isValidBST(TreeNode* root) {
return dfs(root,LLONG_MIN,LLONG_MAX);
}
bool dfs(TreeNode*root,long long floor,long long ceiling){
if(!root)return true;
else if(root->val<=floor||root->val>=ceiling)return false;
else return dfs(root->left,floor,root->val)&&dfs(root->right,root->val,ceiling);
}
};如此便是标准递归做法,这里实际上可以做一些剪枝操作,我们只做了一小部分。下一种实现方式再完成右子树剪枝:
中序遍历
事实上中序遍历本身也是递归的一种。我们这里利用二叉搜索树中序遍历是有序的这个性质,每个结点判断是否严格大于中序遍历的前驱结点:
cpp
class Solution {
public:
long long prev=LLONG_MIN;
bool isValidBST(TreeNode* root) {
if(!root)return true;
bool ret=true;
ret=isValidBST(root->left);
if(!ret)return ret;
if(root->val<=prev)return false;
prev=root->val;
return isValidBST(root->right);
}
};当左子树或者当前结点不满足时,我们执行剪枝操作。
二叉搜索树中第 K 小的元素
题目描述
给定一个二叉搜索树的根节点 root ,和一个整数 k ,请你设计一个算法查找其中第 k 小的元素(k 从 1 开始计数)。
示例 1:
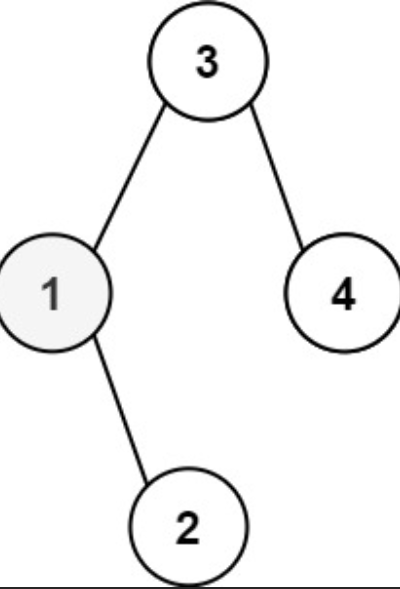
输入:root = [3,1,4,null,2], k = 1
输出:1
示例 2:
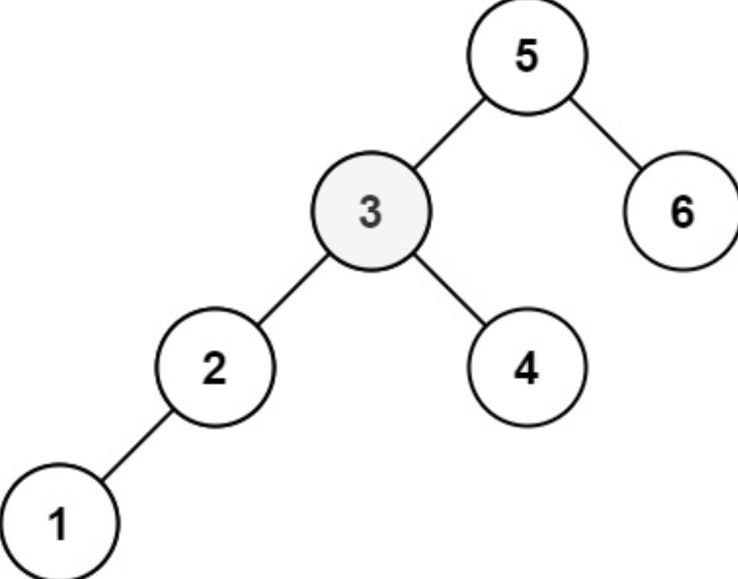
输入:root = [5,3,6,2,4,null,null,1], k = 3
输出:3
提示:
树中的节点数为 n 。
- 1 <= k <= n <= 104
- 0 <= Node.val <= 104
算法原理和实现
根据上一题的思路,我们返回他中序的第k个结点即可,结合剪枝策略:
cpp
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int step=0;
int kthSmallest(TreeNode* root, int k) {
int num;
if(root->left)num=kthSmallest(root->left,k);//还是不要走到空结点为好。
if(step==k)return num;
if(++step==k)return root->val;
if(root->right)return kthSmallest(root->right,k);
return root->val;
}
};二叉树的所有路径
题目描述
给你一个二叉树的根节点 root ,按 任意顺序 ,返回所有从根节点到叶子节点的路径。
叶子节点 是指没有子节点的节点。
示例 1:
输入:root = [1,2,3,null,5]
输出:["1->2->5","1->3"]
算法原理和实现
这是一个简单的回溯,我们判断当前是否为叶子结点,如果是将当前路径加入返回数组中。如果不是向左右子树传递。最后要回退当前值:
cpp
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left),
* right(right) {}
* };
*/
class Solution {
public:
vector<string> binaryTreePaths(TreeNode* root) {
vector<string> ret;
string tmp;
function<void(TreeNode*)>dfs=[&](TreeNode* root){
int len=tmp.size();
tmp+=to_string(root->val);
if(!root->left&&!root->right){
ret.emplace_back(tmp);
}else{
tmp+="->";
}
if(root->left)dfs(root->left);
if(root->right)dfs(root->right);
tmp.resize(len);
};
dfs(root);
return ret;
}
};