
祝大家新年快乐!!!身体健康!!!万事顺意!!!
核心思路
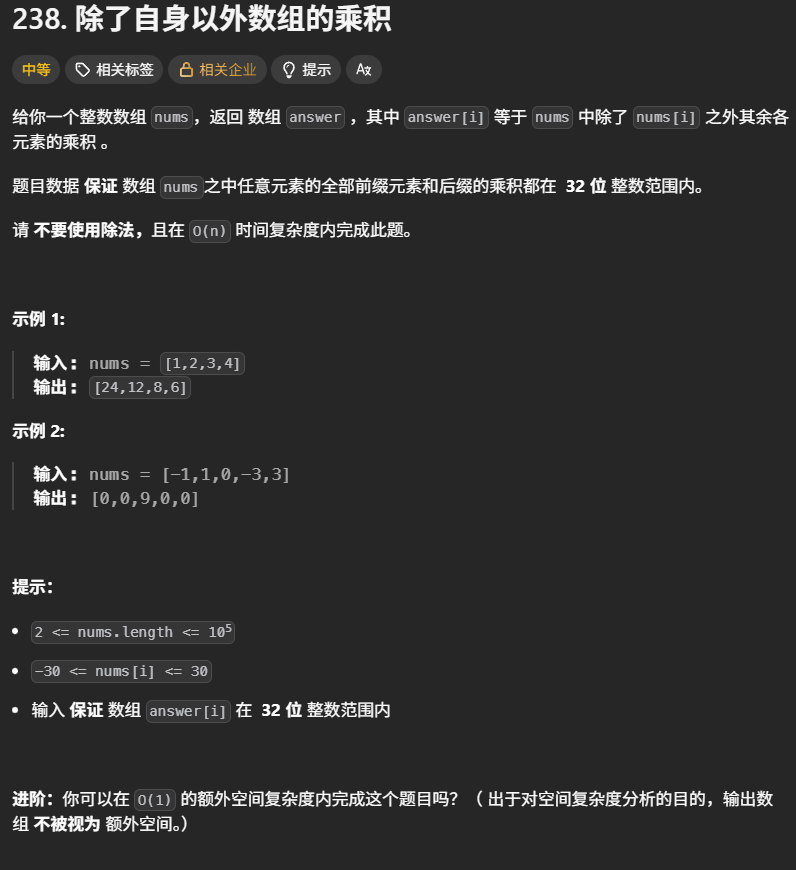
题目要求返回数组 answer,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积,且禁止使用除法,时间复杂度需为 O (n)。
核心解法是前缀积 + 后缀积:
- 前缀积数组 :
prefix[i]表示nums[0] * nums[1] * ... * nums[i-1](即nums[i]左侧所有元素的乘积)。 - 后缀积数组 :
suffix[i]表示nums[i+1] * nums[i+2] * ... * nums[n-1](即nums[i]右侧所有元素的乘积)。 - 最终结果:
answer[i] = prefix[i] * suffix[i]。
解法一:使用前缀积和后缀积数组(空间复杂度 O (n))
实现:
public int[] productExceptSelf(int[] nums) {
int n = nums.length;
int[] prefix = new int[n];
int[] suffix = new int[n];
int[] answer = new int[n];
// 计算前缀积:prefix[i] 是 nums[0..i-1] 的乘积
prefix[0] = 1;
for (int i = 1; i < n; i++) {
prefix[i] = prefix[i - 1] * nums[i - 1];
}
// 计算后缀积:suffix[i] 是 nums[i+1..n-1] 的乘积
suffix[n - 1] = 1;
for (int i = n - 2; i >= 0; i--) {
suffix[i] = suffix[i + 1] * nums[i + 1];
}
// 结果 = 前缀积 * 后缀积
for (int i = 0; i < n; i++) {
answer[i] = prefix[i] * suffix[i];
}
return answer;
}
复杂度分析:
- 时间复杂度:O (n),三次线性遍历。
- 空间复杂度:O (n),使用了两个额外数组。
解法二:原地优化(空间复杂度 O (1),进阶要求)
思路:
- 先用
answer数组存储前缀积。 - 用一个变量
right从右向左遍历,实时维护当前位置的后缀积,直接乘到answer上,从而省去后缀积数组。
实现:
public int[] productExceptSelf(int[] nums) {
int n = nums.length;
int[] answer = new int[n];
// 第一步:计算前缀积,存入 answer 数组
answer[0] = 1;
for (int i = 1; i < n; i++) {
answer[i] = answer[i - 1] * nums[i - 1];
}
// 第二步:从右向左遍历,用变量 right 维护后缀积
int right = 1;
for (int i = n - 1; i >= 0; i--) {
answer[i] = answer[i] * right;
right = right * nums[i]; // 更新后缀积,包含当前元素
}
return answer;
} 示例验证(nums = [1,2,3,4]):
示例验证(nums = [1,2,3,4]):
- 前缀积阶段:
answer = [1, 1, 2, 6] - 从右向左遍历:
- i=3:
answer[3] = 6 * 1 = 6,right = 1 * 4 = 4 - i=2:
answer[2] = 2 * 4 = 8,right = 4 * 3 = 12 - i=1:
answer[1] = 1 * 12 = 12,right = 12 * 2 = 24 - i=0:
answer[0] = 1 * 24 = 24,right = 24 * 1 = 24
- i=3:
- 最终结果:
[24, 12, 8, 6],与示例一致。
复杂度分析:
- 时间复杂度:O (n),两次线性遍历。
- 空间复杂度:O (1),仅使用常数额外空间(输出数组不计入)。
总结
- 基础解法( 左右乘积列表**)**:通过前缀积和后缀积数组,清晰地将问题拆解为 "左侧乘积 × 右侧乘积",易于理解。
- 进阶解法:通过原地复用数组和变量,将空间复杂度优化到 O (1),是面试中的推荐写法。
