Rethinking Network Design and Local Geometry in Point Cloud: A Simple Residual ML (ICLR 2022)
前言
博主导读 :
在 PointNet++ 之后,点云深度学习似乎陷入了一个"内卷"怪圈:大家都在拼命设计更复杂的局部聚合器 (Local Aggregator)。
- DGCNN 引入了动态图卷积;
- PointCNN 搞了 X \mathcal{X} X-Conv 变换矩阵;
- Point Transformer 和 PCT 把注意力机制搬了过来;
- CurveNet 甚至开始在点云里走迷宫(曲线聚合)。
模型越来越重,速度越来越慢,但精度提升却越来越微弱。
PointMLP (ICLR 2022) 是一篇让人"眼前一亮"的反直觉之作。作者提出:我们不需要复杂的卷积或注意力,只要引入一个简单的"几何仿射模块",纯 Residual MLP 就能在精度和速度上双杀 SOTA。
本文将带你拆解这个"重剑无锋"的网络设计哲学。
原文链接:PointMLP: Rethinking Network Design and Local Geometry in Point Cloud Analysis
1. 核心痛点与反思 (Motivation)
1.1 复杂聚合器的代价
现有的 SOTA 方法(如 Point Transformer, CurveNet)虽然在 ModelNet40 上刷到了 93%~94%,但付出的代价是巨大的计算量(FLOPs)和极高的推断延迟(Latency)。很多复杂算子(如 k-NN 建图、Attention Map 计算)在 GPU 上并不友好,存在大量的随机访存。
1.2 MLP 真的不行吗?
PointNet++ 使用了简单的 MLP 来提取局部特征,但它的表现不如后来的图卷积网络。作者反思:是不是因为 MLP 本身不行?还是因为我们没给 MLP 提供好的"输入"?
作者发现,单纯的 MLP 难以捕获局部区域的几何分布差异。如果能把每个局部邻域的数据"归一化"到一个标准姿态,MLP 的学习难度将大幅降低。
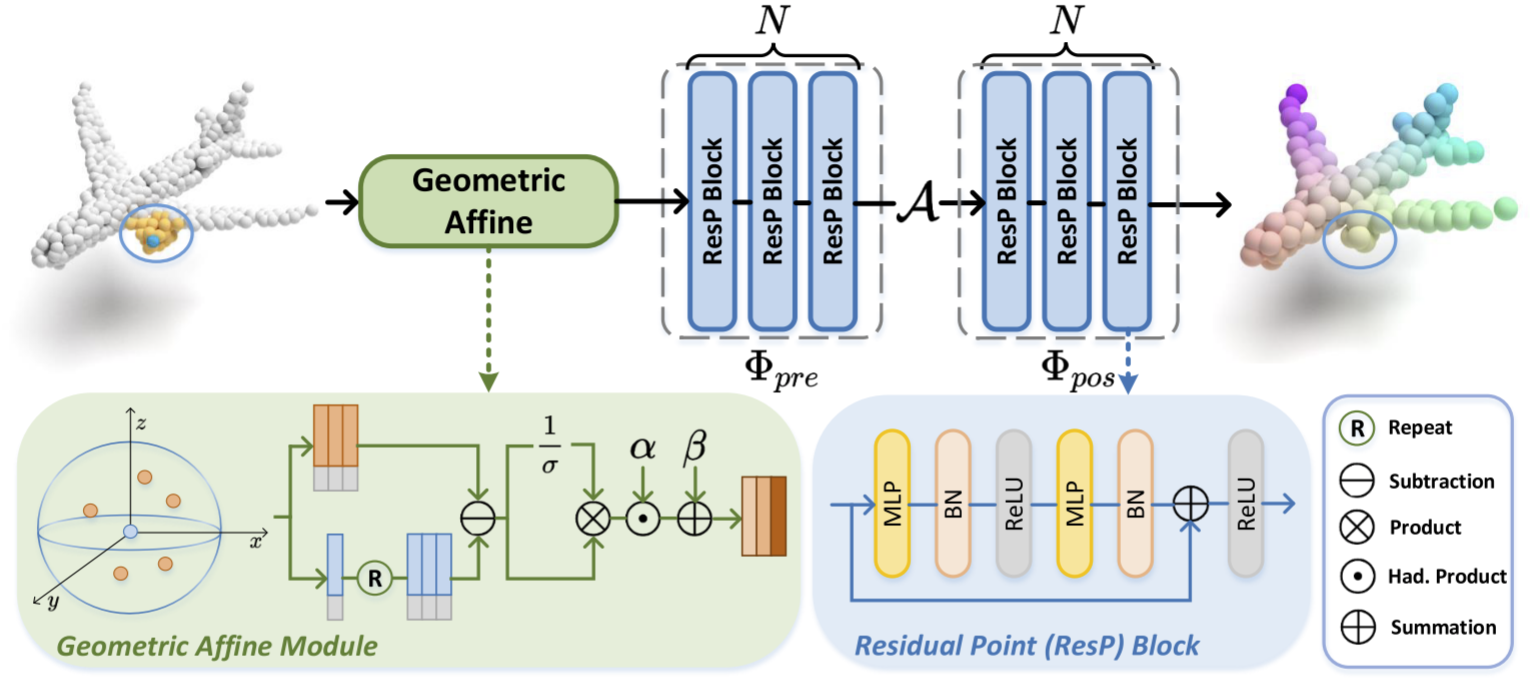
2. 核心魔法:几何仿射模块 (Geometric Affine Module)
PointMLP 的致胜法宝不是复杂的网络结构,而是一个极简的预处理模块:Geometric Affine Module (几何仿射模块)。
2.1 数学原理
假设我们在点云中取了一个局部邻域(Group),包含 k k k 个邻居点 { p i , j ∣ j = 1... k } \{p_{i,j} | j=1...k\} {pi,j∣j=1...k}。由于点云在空间中是任意分布的,不同的局部邻域方差很大。PointMLP 在将这些点送入 MLP 之前,先做如下操作:
1. 标准化 (Standardization) :
计算该邻域内所有特征的方差 σ \sigma σ 和均值(通常用中心点代替),将邻域变换为标准分布:
f i , j = p i , j − p i σ + ϵ f_{i,j} = \frac{p_{i,j} - p_i}{\sigma + \epsilon} fi,j=σ+ϵpi,j−pi
- p i p_i pi: 中心点特征
- p i , j p_{i,j} pi,j: 邻居点特征
- σ \sigma σ: 该邻域内特征的标准差
2. 仿射变换 (Affine Transformation) :
引入两个可学习的参数 α \alpha α (缩放) 和 β \beta β (平移),让网络自己去学习该保留多少几何信息:
f ^ i , j = α ⊙ f i , j + β \hat{f}{i,j} = \alpha \odot f{i,j} + \beta f^i,j=α⊙fi,j+β
🎓解读 :
这步操作看似简单,实则极其关键。它消除了局部区域的平移差异 和尺度差异 。无论这个局部形状是大的还是小的,是在左边还是右边,经过这个模块后,它们都变成了"标准形状"。
MLP 不需要再去死记硬背各种尺度变化,只需要专注于分析形状本身。
3. 网络架构:深层残差 MLP (Deep Residual MLP)
解决了局部输入的标准化问题后,网络架构的设计就变得非常"朴实无华"了。PointMLP 几乎就是 PointNet++ 的分层结构 加上 ResNet 的残差块。
3.1 整体架构
采用典型的 Encoder-Decoder 结构:
- 分层提取:包含 4 个阶段(Stage),点数逐层减少(1024 -> 512 -> 256 -> 128)。
- 特征传播:用于分割任务,采用 FP 模块(同 PointNet++)。
3.2 核心模块:PointMLP Block
不同于 PointNet++ 在每个局部区域只用 1-2 层 MLP,PointMLP 堆叠了深层的 Bottleneck Residual Blocks(瓶颈残差块)。
Input → Geometric Affine → MLP → MLP → Pooling \text{Input} \rightarrow \text{Geometric Affine} \rightarrow \text{MLP} \rightarrow \text{MLP} \rightarrow \text{Pooling} Input→Geometric Affine→MLP→MLP→Pooling
4. PyTorch 核心代码复现
Talk is cheap. 我们来看看这个核心的 Geometric Affine Module 是如何实现的。
python
import torch
import torch.nn as nn
import torch.nn.functional as F
class GeometricAffine(nn.Module):
def __init__(self, dim):
super(GeometricAffine, self).__init__()
# 可学习的仿射参数 alpha 和 beta
self.alpha = nn.Parameter(torch.ones(1, dim, 1, 1))
self.beta = nn.Parameter(torch.zeros(1, dim, 1, 1))
def forward(self, x):
"""
Input:
x: (B, C, N, K) - B:Batch, C:Channel, N:Points, K:Neighbors
这里 x 通常是 (p_neighbors - p_center) 的相对坐标特征
"""
# 1. 计算局部标准差 (Standard Deviation)
# 保持维度为 (B, C, N, 1) 以便广播
std = torch.std(x, dim=-1, keepdim=True)
# 2. 标准化 (Normalize)
# 加上 eps 防止除以 0
x_norm = x / (std + 1e-5)
# 3. 仿射变换 (Affine Transformation)
# 类似于 BatchNorm 的操作,但是是在几何空间
out = self.alpha * x_norm + self.beta
return out结论:
- PointMLP (Elite) :仅用 0.68M 的参数量就达到了 94.0% 的准确率,完胜参数量是其 3 倍的 CurveNet。
- SOTA 表现 :在不考虑参数量限制时,PointMLP 达到了 94.5%,证明了纯 MLP 架构依然可以处于统治地位。
- 推断速度 (Inference Speed) :在同等精度下,PointMLP 的推断速度比 CurveNet 快 3-4 倍。这是因为 MLP 算子在 GPU 上的并行效率远高于 k-NN 或曲线聚合。
6. 总结与思考 (PhD Perspective)
PointMLP 的出现是对点云深度学习领域的一次"降维打击"。它给我们的启示远不止于一个新模型:
1. 基础被低估了 (Don't overlook the basics) :
在大家都在追求复杂的图卷积和 Transformer 时,作者回头重新审视了 MLP。有时候,复杂的不是任务,而是我们设计的模型。
2. 几何归一化是关键 (Geometry matters) :
MLP 并不是不能处理点云,而是需要合适的归一化 (Normalization)。几何仿射模块(Geometric Affine)的作用类似于 CNN 中的 BatchNorm,它让数据分布变得适合网络学习。
3. 残差就是力量 (Residual is all you need) :
只要把 MLP 堆得足够深(借助 ResNet 结构),它的表达能力是惊人的。
📚 附录:MLP点云网络系列导航
本专栏致力于用"人话"解读 3D 点云领域的硬核论文,从原理到代码逐行拆解。
🔥 欢迎订阅专栏 :【点云特征分析_顶会论文硬核拆解】持续更新中...
💬 互动话题 :
现在的 CV 领域,ConvNeXt 和 MLP-Mixer 正在复兴。你觉得在 3D 点云领域,PointMLP 这种"反潮流"的极简设计会成为主流吗?还是说 Transformer 最终会统治一切?
欢迎在评论区留下你的看法!
点赞 👍、收藏 ⭐、关注 🚩 是对博主最大的支持!