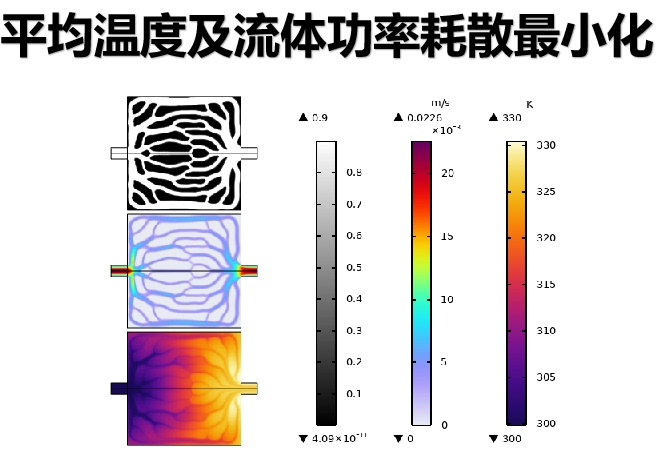
基于Comsol的双目标函数流热拓扑优化液冷板结构设计

基于comsol的双目标函数流热拓扑优化液冷板结构设计，双目标函数为最小平均温度和最小流体功率耗散最小的无量纲化，附赠案例参考文献哈

在电子设备日益小型化和高性能化的今天，散热问题成为了制约其发展的关键因素。液冷板作为一种高效的散热组件，其结构设计对于散热效果和能耗有着至关重要的影响。本文将探讨如何基于Comsol软件，通过双目标函数进行流热拓扑优化，实现液冷板结构的最佳设计。

双目标函数：最小平均温度与最小流体功率耗散

我们设定的双目标函数为最小平均温度和最小流体功率耗散最小的无量纲化。

最小平均温度：确保电子设备工作在适宜温度范围内，防止因过热导致性能下降甚至损坏。
最小流体功率耗散：在保证散热效果的同时，尽量降低能耗，提高能源利用效率。

对这两个目标进行无量纲化处理，能让它们在同一尺度下进行比较和优化，方便我们在优化过程中平衡两者关系。

Comsol实现过程

以下是使用Comsol进行优化的大致步骤，这里以简单的二维模型为例，实际应用中需根据具体情况调整。

1. 建立物理模型

首先，在Comsol中选择合适的物理场接口，如"传热 - 固体"和"传热 - 流体"，分别用于描述固体部分（液冷板本体）和流体部分（冷却液）的传热和流动特性。

comsol 复制代码

// 假设我们已经创建了一个二维几何模型
geom = model.geom('geom1');
// 添加固体传热物理场
ht_solid = model.physics('ht');
// 添加流体传热物理场
ht_fluid = model.physics('htf');

上述代码简单展示了在Comsol中创建几何模型并添加物理场的操作。model.geom('geom1')创建名为geom1的几何对象，然后分别通过model.physics('ht')和model.physics('htf')添加固体传热和流体传热物理场。

2. 设置边界条件

对于液冷板，我们需要设置冷却液入口的流速、温度，以及壁面的边界条件等。

comsol 复制代码

// 设置冷却液入口流速
ht_fluid.bc('inlet').set('u0', 0.1);
// 设置冷却液入口温度
ht_fluid.bc('inlet').set('T0', 300);
// 设置壁面为绝热边界
ht_solid.bc('wall').set('q', 0);

这段代码设置了冷却液入口的流速为0.1 m/s，入口温度为300 K，并将壁面设置为绝热边界条件。ht_fluid.bc('inlet')定位到流体入口边界条件对象，通过.set()方法设置相应参数。

3. 定义双目标函数

在Comsol的优化模块中，定义无量纲化后的最小平均温度和最小流体功率耗散作为目标函数。

comsol 复制代码

// 定义平均温度目标函数
obj1 = model.optimeq('obj1');
obj1.expr = 'avg(T, domain)';
// 定义流体功率耗散目标函数
obj2 = model.optimeq('obj2');
obj2.expr = 'intop1(p*u, boundary)';

这里model.optimeq('obj1')创建名为obj1的优化等式对象，用于定义平均温度目标函数，通过expr属性设置表达式为计算域内温度的平均值。obj2类似地定义了流体功率耗散目标函数，表达式为边界上压力与速度乘积的积分。

4. 进行拓扑优化

利用Comsol的拓扑优化算法，在满足一定约束条件下，对液冷板结构进行优化。

comsol 复制代码

// 设置优化约束条件
model.optcon('con1').set('expr', 'volfrac - 0.5');
// 运行拓扑优化
model.study('std1').run();

上述代码设置了优化约束条件，model.optcon('con1')创建名为con1的优化约束对象，将结构体积分数限制为0.5。最后通过model.study('std1').run()运行优化研究。

案例参考文献

1\] "Thermal - hydraulic performance optimization of liquid - cooled cold plates using multi - objective topology optimization"，该文献详细介绍了基于多目标拓扑优化的液冷板热 - 水力性能优化案例，与本文的双目标优化思路类似，可作为深入研究的参考。 基于comsol的双目标函数流热拓扑优化液冷板结构设计，双目标函数为最小平均温度和最小流体功率耗散最小的无量纲化，附赠案例参考文献哈 通过基于Comsol的双目标函数流热拓扑优化，我们能够在提高液冷板散热效率的同时，降低能耗，为高性能电子设备的散热解决方案提供了更优的设计思路。在实际应用中，需根据具体设备需求和工况进一步调整模型参数和优化策略，以达到最佳效果。 ![](https://i-blog.csdnimg.cn/img_convert/dba4893eed8bb9813ac5f0b1d3b3d3e9.jpeg)