给大模型装一台“事实核查显微镜“：RLFKV 如何用细粒度知识验证治愈金融 RAG 幻觉

给大模型装一台"事实核查显微镜"：RLFKV 如何用细粒度知识验证治愈金融 RAG 幻觉

大模型明明读了研报，还是会把上季度的数据安到本季度头上。金融场景容不得半点含糊------这篇论文把模型回答像查账一样"逐笔核对"，用强化学习训练出一个不敢乱编数字的金融 RAG 系统。

一句话总结

RLFKV 把金融 RAG 的回答拆解为 (实体, 指标, 数值, 时间) 四元组形式的原子知识单元，逐条验证其与检索文档的一致性，验证结果转化为指数衰减的忠实度奖励和二元信息量奖励，通过 GRPO 算法训练模型"说准话"的同时"不能少说话"。在 Qwen3-8B 上将 FDD-ANT 忠实度从 90.2 提升至 93.3，且 83% 的残余错误集中在时间维度。

第一章金融 RAG 的"最后一厘米"困境

RAG 的基本故事大家都听腻了：用户提问 → 检索相关文档 → 大模型据此生成回答。教科书上写到这里就结束了，似乎一切岁月静好。

但金融场景偏偏不是教科书。

看一个真实案例。用户问的是"贵州茅台每股净利润是否达到预期"，系统检索到了一份分析师研报，里面白纸黑字写着"截至 2025 年 3 月 31 日，公司每股收益为 70.86 元"。模型的回答呢？它准确引用了 70.86 元这个数字，但把日期写成了"2025 年 5 月 15 日"。

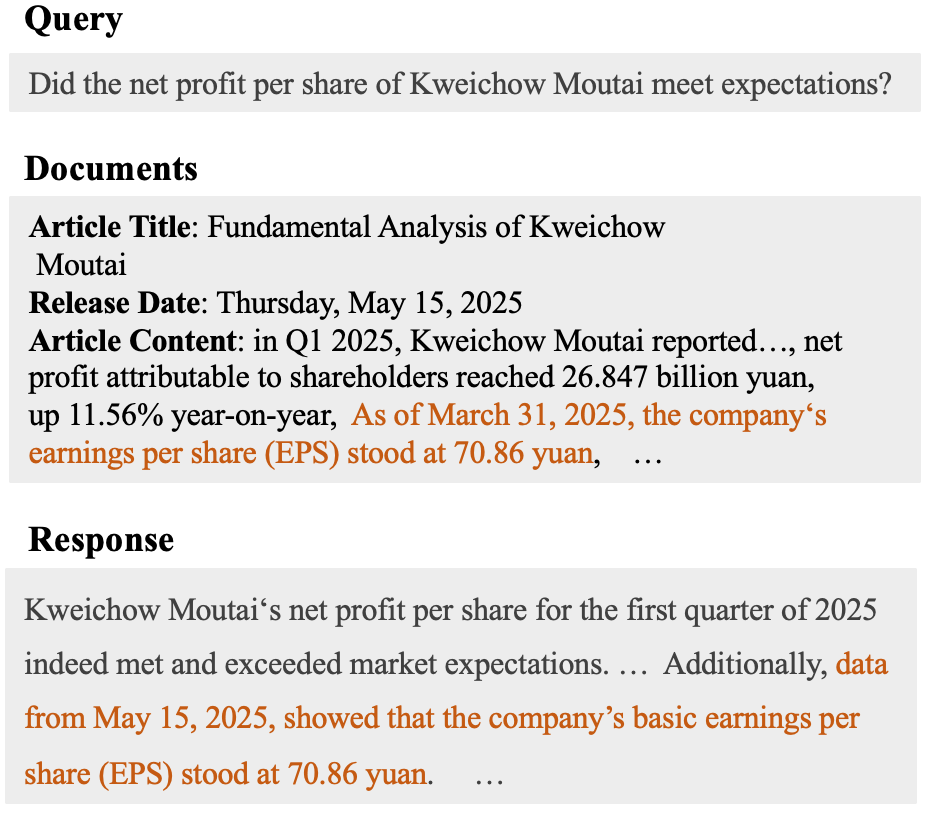
图1：经典的时间归因幻觉。模型正确提取了数值 70.86 元，却把数据截止日期（3月31日）错误替换为文章发布日期（5月15日）。在金融场景中，这两个月的差距可能意味着跨越了一个完整的财报季。

5 月 15 日是什么？那是研报的发布日期，不是数据的截止日期。模型把文档里两个不同语义的日期搞混了。这种错误叫时间归因幻觉------数字本身没编，但把数字"安"到了错误的时间坐标上。

这就好比你让实习生帮你查某只基金上季度的净值，他查到了正确的数字，但写在了本季度的报告里。数字对了，结论全错。在金融领域，一个季度的错位可能意味着用 Q1 数据做了 Q2 的投资决策。

现有解法为什么不够用

最近一年，学术界涌现了一批用 RL 改善 RAG 的工作------DeepRAG、R1-Searcher、R3-RAG 等。它们的共同思路是：训练模型更好地利用检索文档，减少幻觉。但在奖励信号的设计上，它们有两个致命的共性缺陷：

缺陷一：依赖人工标注的参考答案。 金融数据是活的------上周的收盘价、上月的 CPI、上季度的 EPS，每天都在更新。标注一份"标准答案"的成本高不说，这份答案可能下个月就过时了。更要命的是，RAG 系统本来就是为了回答那些"没有固定答案"的问题而存在的，如果都有标准答案了，还要 RAG 干什么？

缺陷二：奖励信号太粗糙。 绝大多数方法用的是二元奖励------整体回答和参考答案匹配就给 1 分，否则给 0 分。但一篇金融分析可能涉及 10 个数据点，模型答对了 9 个、答错了 1 个。在二元奖励的眼里，这和 10 个全答错没有区别，都是 0 分。模型根本不知道自己"哪里对了、哪里错了"。

打一个不太恰当的比方：二元奖励就像高考出分时只告诉你"落榜了"，细粒度奖励则像拿到了每科的成绩单------数学 140 说明数学不用管了，英语 80 说明得加强英语。只有后者才能指导你有效地提升成绩。

第二章 RLFKV 的设计哲学：把"批作文"变成"查账"

RLFKV（Reinforcement Learning with Fine-grained Knowledge Verification）的设计哲学可以用一句话概括：与其笼统地判断"回答对不对"，不如像审计师查账一样，把回答里的每一笔"数据账"都单独核对。

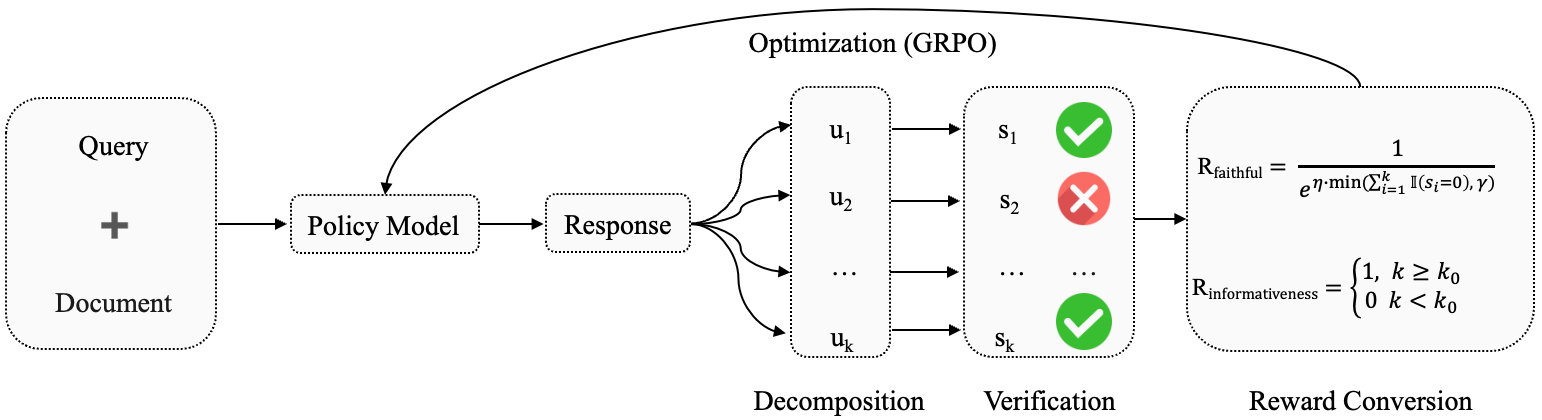
图2：RLFKV 完整流程。策略模型根据查询和检索文档生成回答 → 回答被分解为多个原子知识单元 (u1,u2,...,uk)(u_1, u_2, \ldots, u_k)(u1,u2,...,uk) → 每个单元与检索文档做一致性验证，得到二元分数 (s1,s2,...,sk)(s_1, s_2, \ldots, s_k)(s1,s2,...,sk) → 验证结果转化为忠实度奖励 RfaithfulR_{\text{faithful}}Rfaithful 和信息量奖励 RinformativeR_{\text{informative}}Rinformative → GRPO 算法优化策略模型。

框架分三步：拆解 → 验证 → 奖励驱动训练。每一步都有值得展开的技术细节。

2.1 第一步：把回答拆成"知识原子"------金融四元组

自然语言是高度压缩的。一句"贵州茅台 2025 年 Q1 每股收益 70.86 元，同比增长 11.56%"看起来不长，但其实包含了两个完全独立的事实断言。如果模型在其中一个断言上出了错，我们需要能精确定位是哪一个。

怎么拆？论文借鉴了知识图谱三元组的思路，但做了一个关键的领域适配------提出了金融四元组结构：

原子知识单元=(实体,指标,数值,时间戳)\text{原子知识单元} = (\text{实体}, \text{指标}, \text{数值}, \text{时间戳})原子知识单元=(实体,指标,数值,时间戳)

上面那句话会被拆成：

原子知识单元	实体	指标	数值	时间戳
u1u_1u1	贵州茅台	每股收益(EPS)	70.86元	截至2025年3月31日
u2u_2u2	贵州茅台	净利润同比增长率	11.56%	2025年Q1

为什么是四元组而不是三元组（实体-关系-值）？因为金融数据有一个区别于普通事实的核心特征：时间是不可或缺的语义维度。

"贵州茅台的 EPS 是 70.86 元"------这句话如果不给时间戳，就像说"北京到上海的距离是 1318 公里"一样，看似有信息，实则无法验证。EPS 每个季度都在变，缺了时间戳，你不知道它说的是哪个季度的数据，也就无法判断它对不对。

四元组的四个维度构成了金融事实的完整坐标系：谁（实体）的什么（指标）在何时（时间戳）是多少（数值）。任何一个维度缺失，事实就"悬浮"在半空中，无法和检索文档锚定。

这个思路其实有学术渊源。2023 年 EMNLP 的 FActScore 论文开创了"把生成文本拆成原子事实再逐条验证"的范式。FActScore 处理的是人物传记一类的开放域文本，它的"原子事实"是自然语言句子级别的（比如"爱因斯坦于 1879 年出生在德国乌尔姆"）。RLFKV 的贡献在于把这个思路适配到了金融这个高度结构化的领域，用四元组取代了句子级拆分，粒度更细、验证更精确。

分解过程由一个评估模型 fff 通过 prompt 工程完成：

{ui}i=1k=f(yi)\{u_i\}_{i=1}^{k} = f(y_i){ui}i=1k=f(yi)

论文使用 Qwen3-32B 作为评估模型。prompt 中内置了金融指标字典（EPS、ROE、PE 等标准缩写的对照表），确保不同表述方式的同一指标能被统一识别。比如"每股盈利"和"EPS"应该被视为同一个指标。

2.2 第二步：逐条核查------让评估模型当"审计师"

拆出来的每个原子知识单元，都要回到检索文档里做事实一致性核对：

{si}i=1k=f({ui}i=1k,D)\{s_i\}{i=1}^{k} = f(\{u_i\}{i=1}^{k}, \mathcal{D}){si}i=1k=f({ui}i=1k,D)

si∈{0,1}s_i \in \{0, 1\}si∈{0,1}，1 代表该单元与文档一致，0 代表不一致。

验证同样由 Qwen3-32B 完成。你可以把这个过程想象成会计事务所的审计流程：一个审计师拿着公司给的财务报告（模型回答），一行一行地和银行流水、发票原件（检索文档）做比对。每一笔账都要核------金额对不对、日期对不对、科目对不对。

回到前面的例子，审计师核对 u1=(贵州茅台,EPS,70.86,2025年5月15日)u_1 = (\text{贵州茅台}, \text{EPS}, 70.86, 2025\text{年}5\text{月}15\text{日})u1=(贵州茅台,EPS,70.86,2025年5月15日) 时，翻阅检索文档发现写的是"截至 2025 年 3 月 31 日"，时间戳不匹配，标记 s1=0s_1 = 0s1=0。

这种逐条核查的粒度才是 RLFKV 和之前方法的本质区别。之前的方法是"看一眼报表觉得大致没问题就签字了"，RLFKV 是"每一行每一列都查"。

2.3 第三步：双重奖励------既罚"说错话"又罚"不说话"

核查结果怎么变成训练信号？这是整个框架最精妙的设计。论文不是简单地把正确率当奖励，而是设计了两个奖励函数，分别解决两个截然不同的问题。

忠实度奖励 rfr_frf：指数衰减惩罚

rf=1eη⋅min⁡(score,γ)r_f = \frac{1}{e^{\eta \cdot \min(\text{score}, \gamma)}}rf=eη⋅min(score,γ)1

其中 score=∑i=1kI(si=0)\text{score} = \sum_{i=1}^{k} \mathbb{I}(s_i = 0)score=∑i=1kI(si=0)，即错误的原子知识单元数量。η\etaη 是衰减系数，γ\gammaγ 是错误数量的上限。

这个公式背后有两层考量：

指数衰减而非线性惩罚。 犯 0 个错和犯 1 个错，奖励差距不大（从 1.0 降到约 0.37）。但犯 3 个错和犯 5 个错，差距急剧拉大。为什么这么设计？因为从 1 个错降到 0 个错是"最后的精打细磨"，难度最高；而从 5 个错降到 3 个错是"先把最明显的低级错误消灭"，难度较低。指数衰减让模型优先修正那些容易修正的错误，符合训练的自然节奏。

错误上限 γ\gammaγ。 假设一个回答有 15 个原子知识单元全部错误。没有上限的话，rf≈e−15ηr_f \approx e^{-15\eta}rf≈e−15η，这个数字接近于零。在 RL 训练中，极小的奖励意味着极小的梯度，模型"学不动"。设了上限 γ\gammaγ 后，无论错多少，惩罚都不会超过某个阈值，保证梯度始终有意义。这就好比老师改卷子，0 分和 -10 分没有本质区别------重点是让学生知道"这份答案问题很大"，而不是"问题大到绝望"。

信息量奖励 rir_iri：防止奖励黑客

ri={1if k≥k00otherwiser_i = \begin{cases} 1 & \text{if } k \geq k_0 \\ 0 & \text{otherwise} \end{cases}ri={10if k≥k0otherwise

kkk 是策略模型当前回答中的原子知识单元数量，k0k_0k0 是训练前基础模型在同一问题上生成的数量。

这个看似简单的二元约束，解决的是 RL 训练中一个臭名昭著的问题------奖励黑客（Reward Hacking）。

设想一下：如果只有忠实度奖励，模型的最优策略是什么？是回答"贵州茅台表现良好"然后句号收尾。零个数据点，零个错误，忠实度奖励满分。这就像考试时交白卷不会扣分一样荒谬------虽然没有答错任何题，但也没有回答任何问题。

信息量奖励设了一条底线：你回答中包含的信息密度不能低于训练前的水平。想拿高分？不许靠"闭嘴"，只能靠"说准"。

这种"少说少错"的策略在 RL 文献中有个正式名字叫"退化策略"（degenerate policy）。很多 RL 训练失败案例的根源都是模型找到了某种"钻空子"的方式来最大化奖励而不真正完成任务。RLFKV 的信息量奖励就是专门堵这个漏洞的。

总奖励与 GRPO 优化

总奖励是两者的算术平均：

r=rf+ri2r = \frac{r_f + r_i}{2}r=2rf+ri

优化算法选用 GRPO（Group Relative Policy Optimization），这是 DeepSeek 在 DeepSeekMath 论文中提出的。GRPO 相比传统 PPO 的最大改进是去掉了 Critic 网络。

传统 PPO 需要一个 Critic 模型来估计每个状态的"基线价值"，这实质上是同时训练两个大模型------一个 Actor（策略模型）和一个 Critic（价值模型），计算开销翻倍。GRPO 的做法巧妙得多：对同一个 query，用策略模型生成 N=8N=8N=8 个回答，分别计算奖励，然后用这 8 个奖励的均值和标准差做归一化。

A^i=ri−rˉσr+ϵ\hat{A}_i = \frac{r_i - \bar{r}}{\sigma_r + \epsilon}A^i=σr+ϵri−rˉ

奖励高于均值的回答是正样本（"你比同组平均水平好，继续这么做"），低于均值的是负样本（"你比同组平均水平差，别这么做了"）。不需要外部的 Critic 来告诉模型"绝对好坏"，只需要组内的"相对排名"。

完整的优化目标：

L=E[∑i=1Nπθ(ai∣s)πθold(ai∣s)⋅A^i−β⋅KL(πθ∥πθold)]\mathcal{L}=\mathbb{E}\left[\sum_{i=1}^{N}\frac{\pi_{\theta}(a_{i}|s)}{\pi_{\theta_{\text{old}}}(a_{i}|s)}\cdot\hat{A}i-\beta\cdot\text{KL}(\pi{\theta}\parallel\pi_{\theta_{\text{old}}})\right]L=E[i=1∑Nπθold(ai∣s)πθ(ai∣s)⋅A^i−β⋅KL(πθ∥πθold)]

KL 散度项确保新策略不会偏离旧策略太远，防止训练不稳定。

在 RLFKV 的场景下，GRPO 还有一个额外的好处：每个回答都需要调用 Qwen3-32B 做知识单元分解和验证，本身的计算开销就不低。如果再叠一个和策略模型同等规模的 Critic 网络，训练成本会膨胀到不切实际。GRPO 通过"自比较"替代"外部基线"，是一个工程上极为务实的选择。

第三章实验：细粒度奖励到底能带来多大收益

3.1 实验设置

数据集。 论文使用了两个评测集：

数据集	来源	样本数	覆盖范围
FDD	BizFinBench 公开基准	1,461	个股数据描述
FDD-ANT	论文新构建	2,000	个股 + 基金 + 宏观经济指标（CPI、GDP等）

FDD-ANT 是本文的新贡献。原始 FDD 只覆盖股票数据，但现实中的金融分析师不可能只看股票------基金净值、宏观指标、行业数据都是日常工作的一部分。FDD-ANT 填补了这个覆盖面的空白。

训练数据是额外收集的约 4,000 个样本，和两个评测集没有重叠。

模型。 策略模型用 Qwen3-8B 和 LLaMA3.1-8B-Instruct 两个基线；评估模型（负责知识单元分解和验证）用 Qwen3-32B；最终评测用 GPT-4o 做裁判。

训练配置。 8 张 NVIDIA H20 GPU，学习率 1e-6，训练 1 个 epoch，最大响应长度 2048 tokens，使用 ms-swift 训练框架。值得一提的是，H20 不是最顶级的 GPU（算力大约是 A100 的 60%），这说明 RLFKV 对硬件的要求并不苛刻。

评测维度。 GPT-4o 从两个角度打分：

忠实度：回答与检索文档的一致程度，三档------完全正确（100分）、部分正确（60分）、有重大错误（0分）
信息量：回答中原子知识单元的数量，反映回答的信息密度

3.2 主实验结果

模型	FDD 忠实度	FDD 信息量	FDD-ANT 忠实度	FDD-ANT 信息量
DeepSeek V2 Lite (16B)	69.1	8.8	76.1	5.4
LLaMA3-8B	80.0	11.4	80.5	6.5
Qwen3-8B	86.5	13.4	90.2	10.8
Xuanyuan3 (13B, 金融专用)	57.8	7.9	64.6	5.8
Dianjin-R1 (7B, 金融专用)	78.3	10.8	84.7	6.8
RLFKV (LLaMA3)	83.6	11.7	82.1	8.1
RLFKV (Qwen3)	89.5	13.5	93.3	12.3

几个值得掰开来看的发现：

发现一：RLFKV 带来稳定一致的提升。 Qwen3 基线在 FDD-ANT 上已经高达 90.2 分，RLFKV 还能往上推 3.1 分到 93.3。在更弱的 LLaMA3 上，FDD 忠实度从 80.0 到 83.6，涨幅 3.6 分。两个不同底座、两个不同数据集，提升幅度都在 1.6~4.8 分之间，说明方法本身具有鲁棒性，不依赖特定的模型架构或数据分布。

发现二：金融专用模型的表现令人意外。 Xuanyuan3 是 13B 参数的金融领域大模型，忠实度却只有 57.8（FDD），比 8B 参数的通用模型 Qwen3 低了近 30 分。这不是个例------另一个金融模型 Dianjin-R1 的表现也不如 Qwen3。

这背后有一个反直觉但逻辑自洽的解释：金融专用模型通过 SFT 记住了大量金融"知识"（历史财报数据、行业趋势等）。当它收到一个关于茅台 EPS 的问题时，脑子里已经有了一个"记忆中的 EPS 值"。这个记忆值和检索文档中的最新值可能不一样（因为训练数据有时滞）。模型在两个信息源之间做选择时，可能倾向于用自己的"记忆"------毕竟是 SFT 强化过的。

这就好比一个记忆力超群的财务分析师，每次做尽职调查时总是依赖自己的记忆而不是翻看最新的审计报告。他"知道"得越多，反而越容易出错------因为他记住的是去年的数据。

发现三：信息量也在增长。 RLFKV (Qwen3) 的信息量从 10.8 涨到 12.3，说明模型不仅变得更准确了，还变得更愿意"说话"了。这直接证明信息量奖励发挥了作用------模型没有走"少说少错"的捷径。

3.3 消融实验：每个组件的贡献

信息量奖励的价值

模型变体	FDD 忠实度	FDD 信息量	FDD-ANT 忠实度	FDD-ANT 信息量
RLFKV (LLaMA3)	83.6	11.7	82.1	8.1
去掉信息量奖励	83.2	10.3	81.4	7.0
RLFKV (Qwen3)	89.5	13.5	93.3	12.3
去掉信息量奖励	89.0	12.0	91.9	11.2

去掉信息量奖励后，忠实度只微降 0.4~1.4 分，但信息量大幅下降 1.1~1.5 分。

数据清晰地说明了一件事：只优化"说准"而不约束"说多少"，模型确实会变懒。 忠实度几乎不变，但模型学会了用更短、更保守的回答来规避犯错的风险。信息量奖励像安全绳，防止模型往"空洞回答"的方向滑落。

细粒度 vs 粗粒度奖励

这组对比是全文最有说服力的实验。

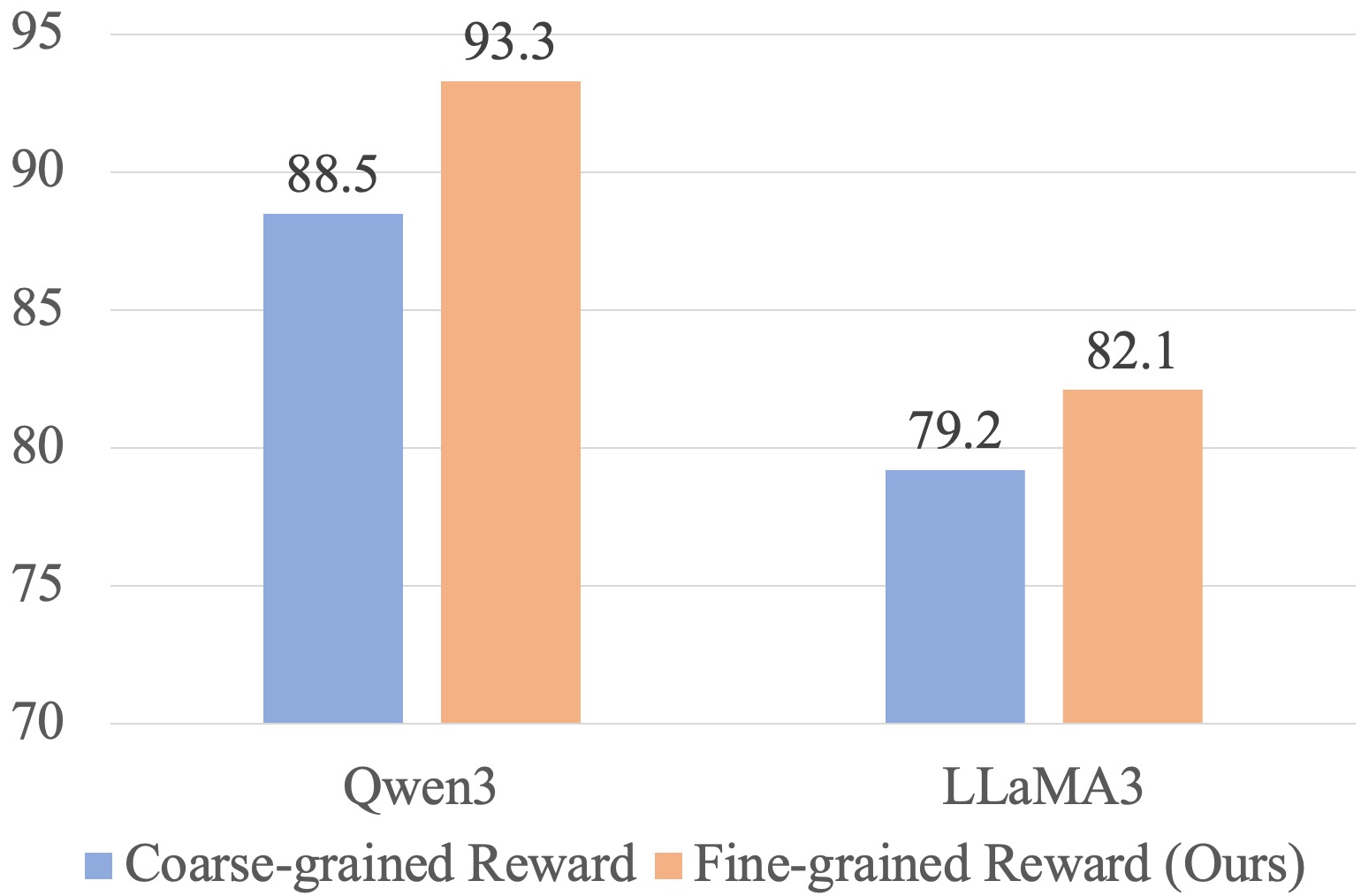
图3(a)：在 FDD-ANT 上，细粒度奖励（橙色）全面优于粗粒度奖励（蓝色）。Qwen3 上差距为 93.3 vs 88.5（+4.8），LLaMA3 上为 82.1 vs 79.2（+2.9）。

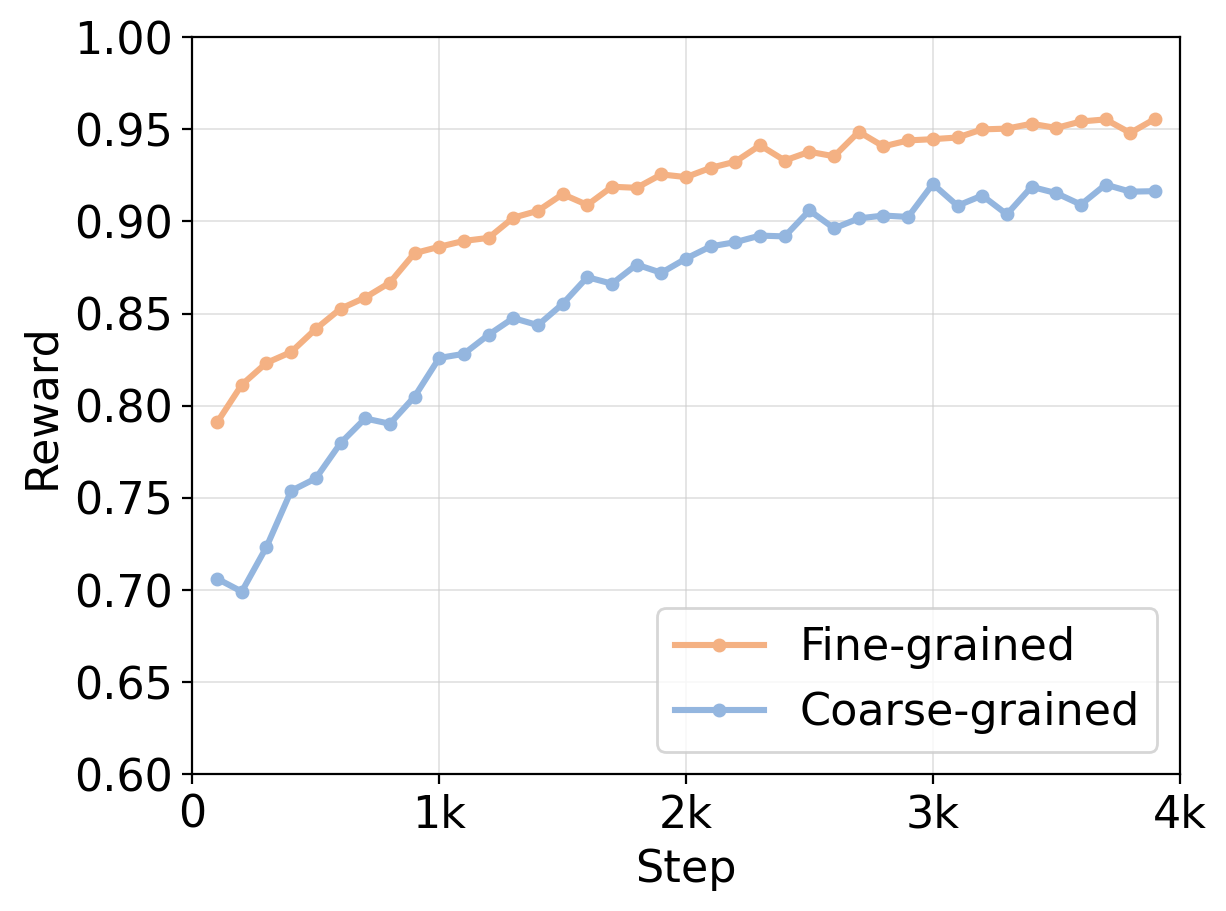
图3(b)：训练奖励曲线。细粒度奖励（橙线）起点更高（约0.79），在约2000步即收敛至0.95附近，曲线平滑；粗粒度奖励（蓝线）起点更低（约0.70），波动剧烈，在约4000步才趋于稳定。

两个关键观察：

效果更好。 在已经 88 分以上的高分区间，细粒度奖励还能再提升近 5 分，这个增量是显著的。粗粒度奖励就像一个只会说"好"或"不好"的评委，模型很难从中提取出精确的改进方向。细粒度奖励则像一个逐项打分的评委，模型清楚地知道哪些数据点做对了可以保持，哪些做错了需要改。

训练更稳定。 粗粒度奖励的曲线波动剧烈，原因很直观：一个回答里 9 个数据点正确、1 个错误，和 5 个正确、5 个错误，在二元奖励下得到的反馈是一样的（都"有错误"= 0）。这种"信息丢失"导致梯度的方差很大。细粒度奖励保留了"9/10 正确"和"5/10 正确"之间的差异，梯度信号更平稳，训练收敛更快。

如果把粗粒度奖励比作 GPS 导航只告诉你"你偏离了路线"，那细粒度奖励就是告诉你"你偏离了路线，往右偏了 200 米，需要在下个路口左转"。两者的信息量级不在一个层面上。

3.4 错误分析：时间是最后的堡垒

即便经过 RLFKV 优化，模型仍然会犯错。论文对残余错误做了分类，结果引人深思。

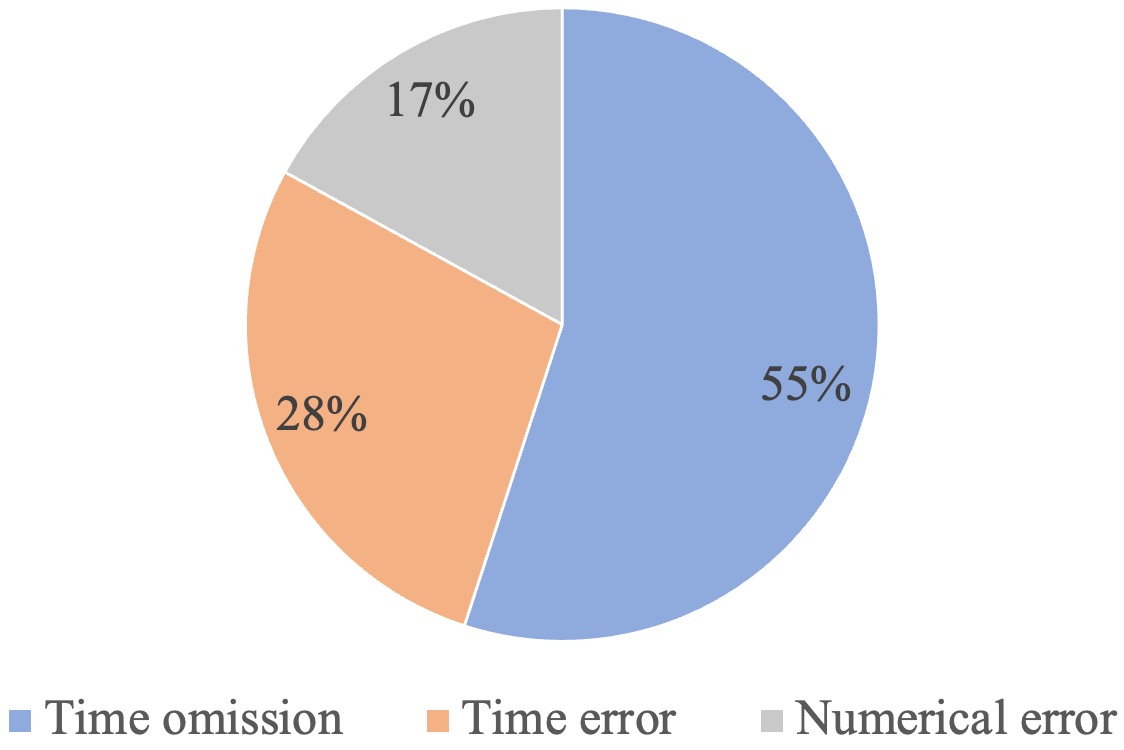
图4：残余错误中，时间遗漏占 55%，时间不准确占 28%，数值错误仅占 17%。时间相关错误合计占比高达 83%。

错误类型	占比	描述	典型示例
时间遗漏	55%	回答中缺少时间限定	"茅台EPS为70.86元"（缺少"截至2025年3月31日"）
时间不准确	28%	时间表述有误	财年与自然年混淆、相对时间解析错误
数值错误	17%	数字有误	四舍五入精度不够、单位换算出错

83% 的残余错误和时间有关。模型最容易搞砸的不是数字本身，而是数字的时间坐标。

这个现象值得深入思考。为什么时间这么难？一篇金融研报里通常包含多个时间维度的数据------"2025 年 Q1 的 EPS"、"2024 年同期的 EPS"、"同比增长率"（隐含了两个时间点）、"截至报告日"（又一个时间点）。模型需要在这些密集的时间信息中精确地为每个数值"匹配"到正确的时间戳，难度比提取数值本身高得多。

更微妙的是，时间遗漏（55%）比时间错误（28%）更常见。模型不是"搞错了时间"，而是"干脆不提时间"。这可能是忠实度奖励的一个副作用------模型学到了"说错时间会被惩罚"，于是干脆选择"不说时间"来避免惩罚。当前的信息量奖励只约束了原子知识单元的总数量，没有约束每个单元的完整性（四元组是否四个维度都齐全）。

第四章与相关工作的定位

方法	是否需要参考答案	奖励粒度	适用领域	核心创新
DeepRAG	需要	粗粒度（二元）	通用	自适应检索决策
R1-Searcher	需要	粗粒度（二元）	通用	搜索式推理
R3-RAG	需要	粗粒度（二元）	通用	检索-反思-回答循环
FActScore	不需要	细粒度（原子事实）	通用	原子事实分解+验证
RLFKV	不需要	细粒度（四元组）	金融	领域适配的原子知识单元 + 双重奖励 + GRPO训练

RLFKV 在两个维度上实现了差异化：

不依赖参考答案。 验证的对象是检索文档，而不是标注的"标准答案"。这在数据快速更新的金融场景下是决定性的优势------你不需要维护一个永远在过期的答案库。
领域适配的细粒度奖励。 相比 FActScore 的句子级原子事实，金融四元组的粒度更细、验证更精确。一个句子级的原子事实"贵州茅台 2025Q1 的 EPS 为 70.86 元"在 FActScore 框架下是一个整体，要么对要么错。但在四元组框架下，它被拆成了四个可独立验证的维度------即使实体、指标、数值都对了，时间戳错了也能被精确定位。

第五章我的思考与工程建议

思考一：四元组是这篇论文最值得借鉴的设计

好的工程设计往往不是做了什么高深的事情，而是找到了恰当的抽象层次。四元组 (实体, 指标, 数值, 时间) 抓住了金融事实最核心的四个维度------既不过于粗糙（句子级判断会放过很多细微错误），也不过于精细（如果把字体格式、措辞风格都当维度，验证成本会爆炸）。

这个抽象层次是可以迁移到其他垂直领域的：

医疗：(患者/群体, 指标, 数值, 检查时间) ------ "患者张某 2025年1月的空腹血糖为 6.2 mmol/L"
法律：(当事人, 条款/行为, 金额/结果, 日期) ------ "被告于 2024年6月未按合同支付 50万元"
供应链：(商品, 指标, 数值, 时间) ------ "A 产品在 2025年3月的库存周转率为 8.2 次"

核心原则是：找到目标领域中构成"一个完整事实"所必需的最小维度集合，然后按这些维度做原子化拆解。

思考二：金融专用模型在 RAG 忠实度上的"知识诅咒"

Xuanyuan3（金融专用 13B）在 FDD 上只有 57.8 分，比通用的 Qwen3（8B）低了近 30 分。这个实验结果需要被认真对待------它暗示了一个在 RAG 系统设计中被广泛忽视的矛盾：模型的领域知识越丰富，它在 RAG 场景下的忠实度可能越低。

这和日常经验中"专家更可靠"的直觉相悖。但换个角度想：一个经验丰富的基金经理，你给他一份最新的研报让他据此写分析，他很可能会不自觉地混入自己的经验判断和过往记忆，而不是老老实实地只引用研报内容。一个刚入行的新人反而会更忠实地"照本宣科"。

在 RAG 系统设计中，这意味着"模型能力强"和"模型忠实度高"不是同一件事。对于需要严格依据检索文档回答问题的场景（比如金融合规、法律尽调），可能需要在模型选择和训练策略上做特殊考量，甚至有意识地"抑制"模型的先验知识。

思考三：评估模型的可靠性是一个没有展开的隐忧

整个 RLFKV 框架的"验证"步骤依赖 Qwen3-32B 作为评估模型。一个自然的问题是：如果评估模型本身的验证准确率只有 90%，那 10% 的验证结果是噪声。在一个包含 10 个原子知识单元的回答中，平均有 1 个单元的验证标签是错误的。这个噪声会通过奖励信号传递到策略模型的训练过程中。

论文没有报告评估模型自身的验证准确率，也没有做"评估模型准确率 vs RLFKV 最终性能"的敏感性分析。这是一个遗憾。从实验结果看，方法整体有效，说明当前的噪声水平在可承受范围内------但如果要把这个框架推广到评估模型更不可靠的场景（比如小语种金融数据），评估模型的质量可能成为瓶颈。

一个可能的改进方向是引入多评估模型投票：用 2-3 个不同的评估模型分别验证，取多数意见。这会增加推理成本，但能显著降低噪声。

思考四：时间遗漏是信息量奖励的"漏网之鱼"

前面提到 55% 的残余错误是时间遗漏------模型给出了正确的实体、指标、数值，但"忘了"说时间。这种情况下，四元组是不完整的（只有三个维度有值），忠实度奖励无法惩罚一个"不存在的错误"（它没说错时间，只是没说），而信息量奖励只看总的原子知识单元数量，不看每个单元是否完整。

一个直觉的改进方案：在忠实度验证中增加一条规则------如果一个原子知识单元的四元组有维度缺失，视为不完整，给一个折扣分（比如 0.5 而不是 1）。这样模型就有动力补全时间戳，而不是省略它来规避惩罚。

工程落地建议

如果你在构建金融 RAG 系统（或任何需要高忠实度的垂直领域 RAG），以下几点可以直接借鉴：

1. 推理时加一层"逐条核查"后处理。 即便不做 RL 训练，在模型生成回答后，用一个较强的模型（如 GPT-4o 或 Qwen3-32B）把回答拆成原子知识单元，逐条和检索文档比对。标记出不一致的部分，要么自动修正，要么提示用户注意。这个步骤的成本远低于 RL 训练，但能显著提升输出质量。

2. 在 prompt 中显式强调时间维度。 83% 的残余错误与时间有关。在系统 prompt 中加入类似"回答中涉及的每个数据点都必须标明数据对应的时间信息，不要省略时间"的约束，可能是性价比最高的单点改进。

3. 警惕"越专业越不忠实"的陷阱。 如果你用金融领域 SFT 模型做 RAG 基座，务必测试它的忠实度是否反而下降了。一个简单的测试方法：准备 100 个问题，故意让检索文档中的数据和模型训练数据中的数据有冲突，看模型倾向于引用文档还是用自己的"记忆"。

4. 如果做 RL 训练，一定要加信息量约束。 这个教训不仅适用于金融场景------任何只优化准确率的 RL 训练，模型都可能学会"少说话"来规避犯错。信息量约束的具体形式可以调整（不一定是二元的），但"得有"这一点是刚性的。

5. 考虑分阶段训练。 先用细粒度忠实度奖励解决数值层面的错误，再用专门针对时间维度的奖励解决时间遗漏和时间错误。当前框架对四个维度"一视同仁"，但从错误分布看，时间维度明显是短板，可能需要单独加大权重。

论文关键信息卡

项目	内容
标题	Mitigating Hallucination in Financial RAG via Fine-Grained Knowledge Verification
核心贡献	RLFKV 框架（金融四元组分解 + 细粒度验证 + 双重奖励 + GRPO）、FDD-ANT 数据集
策略模型	Qwen3-8B、LLaMA3.1-8B-Instruct
评估模型	Qwen3-32B（知识单元分解与验证）、GPT-4o（最终评测）
优化算法	GRPO（每 query 采样 N=8 个回答）
关键结果	Qwen3 忠实度：86.5→89.5 (FDD)、90.2→93.3 (FDD-ANT)；细粒度 vs 粗粒度：93.3 vs 88.5
训练配置	8 × NVIDIA H20 GPU，lr=1e-6，1 epoch，ms-swift 框架
数据规模	训练 4,000 样本；评测 FDD 1,461 + FDD-ANT 2,000 样本
论文链接	https://arxiv.org/abs/2602.05723

给大模型装一台“事实核查显微镜“：RLFKV 如何用细粒度知识验证治愈金融 RAG 幻觉