时间复杂度 - 技术栈

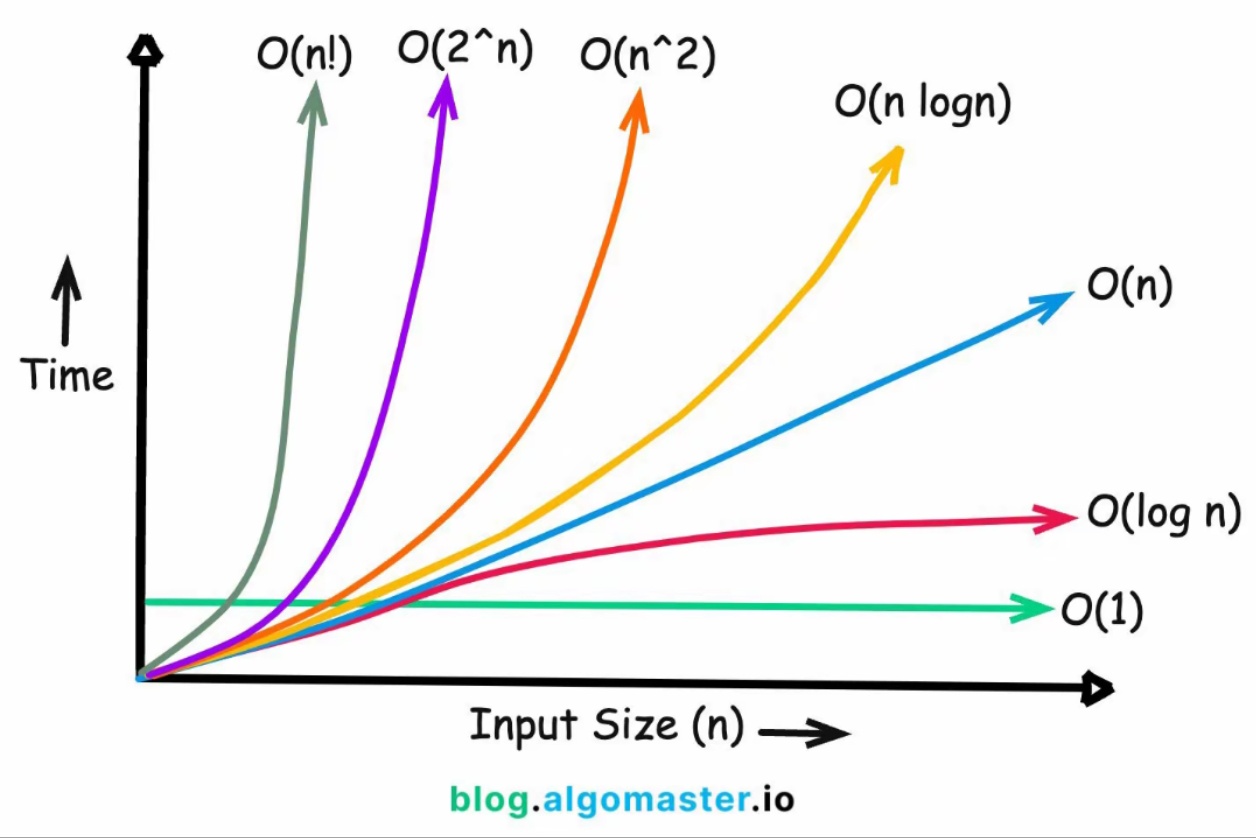
图1

图2

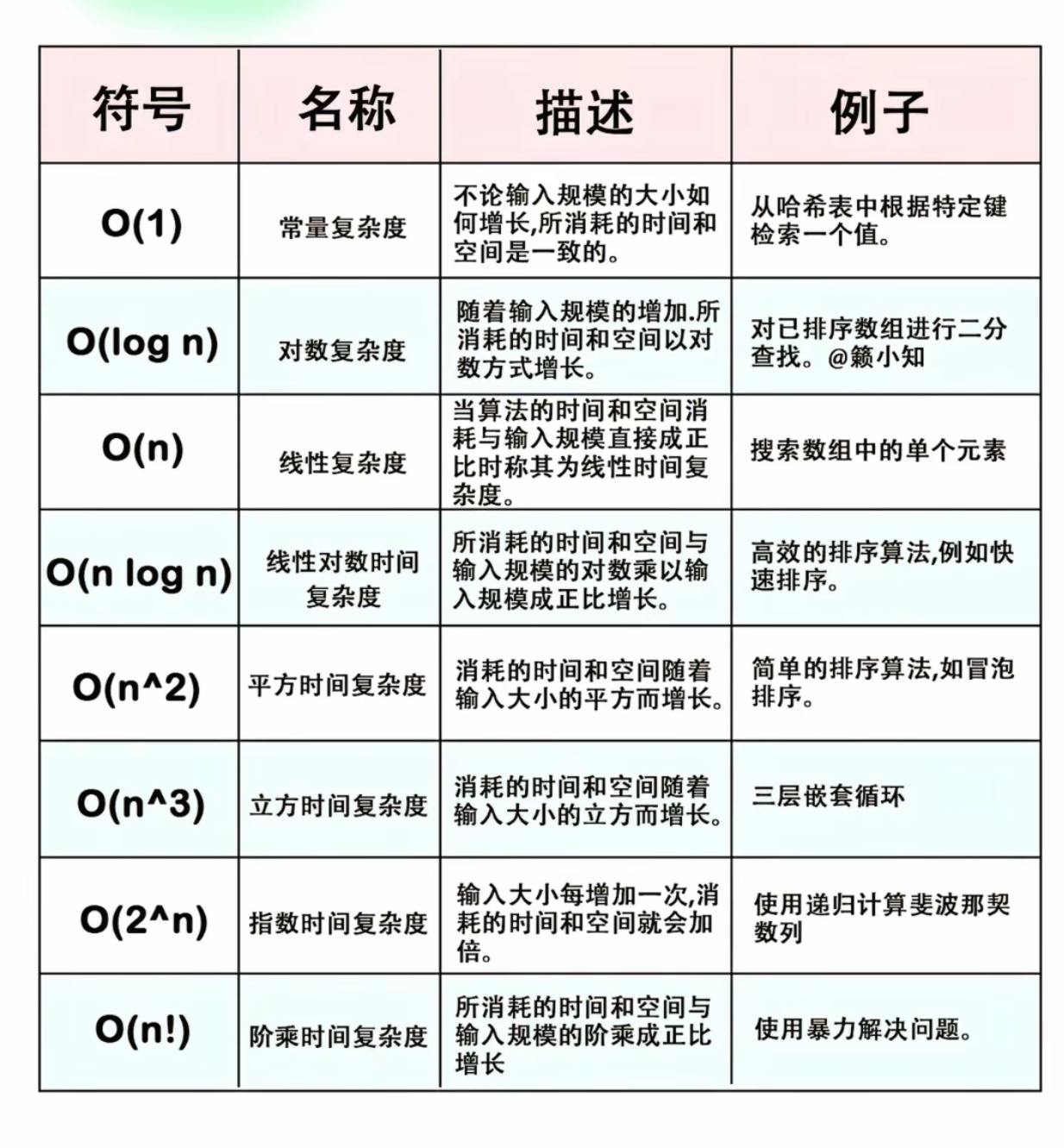
这个的时间复杂度和空间复杂度是多少

复制代码

const a = [1, 2, 3, 4, 5, 6, 7, 8]
a.forEach(element => {
  console.log(element)
});
a.forEach(element => {
  console.log(element)
});

时间复杂度是O(n),空间复杂度是O(1)[没有开辟新的内存空间]

代码中连续调用了两次 forEach，总操作次数是 n + n = 2n。

但在时间复杂度分析中，常数系数会被忽略 （因为复杂度关注的是 "随数据量增长的趋势"，而非具体次数），因此 2n 仍记为 O(n)。

简单理解：不管是遍历 1 次还是 100 次，只要是固定次数的遍历，时间复杂度都是 O (n)；只有嵌套遍历（比如 for 里套 for）才会变成 O (n²)

1. 时间复杂度为 O (log n) 的代码示例（二分查找）

二分查找是典型的 O (log n) 时间复杂度算法，每次轮操作都会将问题规模缩小一半。

二分查找算法（O(log n)）

复制代码

/**
 * 二分查找：在有序数组中查找目标值
 * @param {number[]} nums 有序数组
 * @param {number} target 目标值
 * @return {number} 目标值索引，未找到返回-1
 */
function binarySearch(nums, target) {
    let left = 0;
    let right = nums.length - 1;
    
    // 每轮循环将搜索范围缩小一半
    while (left <= right) {
        const mid = Math.floor((left + right) / 2);
        
        if (nums[mid] === target) {
            return mid; // 找到目标，返回索引
        } else if (nums[mid] < target) {
            left = mid + 1; // 目标在右侧
        } else {
            right = mid - 1; // 目标在左侧
        }
    }
    
    return -1; // 未找到目标
}

// 示例
const arr = [1, 3, 5, 7, 9, 11, 13];
console.log(binarySearch(arr, 7)); // 输出: 3（7在数组中的索引）
console.log(binarySearch(arr, 4)); // 输出: -1（4不在数组中）

时间复杂度分析 ：每次循环都会将搜索范围从 n 缩小到 n/2，再到 n/4... 直到范围为 1，总循环次数为 log₂n，因此时间复杂度为 O (log n)。

2. 时间复杂度为 O (n log n) 的代码示例（归并排序）

归并排序是典型的 O (n log n) 时间复杂度算法，通过分治策略将数组拆分后合并，拆分过程是 O (log n)，合并过程是 O (n)。

归并排序算法（O(n log n)）

复制代码

/**
 * 归并排序：将数组递归拆分为子数组，再合并为有序数组
 * @param {number[]} arr 待排序数组
 * @return {number[]} 排序后的数组
 */
function mergeSort(arr) {
    // 递归终止条件：数组长度为1时无需排序
    if (arr.length <= 1) {
        return arr;
    }
    
    // 拆分：将数组分为两半（O(log n) 层拆分）
    const mid = Math.floor(arr.length / 2);
    const left = mergeSort(arr.slice(0, mid)); // 左半部分递归排序
    const right = mergeSort(arr.slice(mid));   // 右半部分递归排序
    
    // 合并：将两个有序数组合并为一个有序数组（每层合并总耗时O(n)）
    return merge(left, right);
}

/**
 * 合并两个有序数组
 * @param {number[]} left 有序数组1
 * @param {number[]} right 有序数组2
 * @return {number[]} 合并后的有序数组
 */
function merge(left, right) {
    const result = [];
    let i = 0, j = 0;
    
    // 比较两个数组的元素，按顺序放入结果数组
    while (i < left.length && j < right.length) {
        if (left[i] <= right[j]) {
            result.push(left[i]);
            i++;
        } else {
            result.push(right[j]);
            j++;
        }
    }
    
    // 处理剩余元素
    while (i < left.length) {
        result.push(left[i]);
        i++;
    }
    while (j < right.length) {
        result.push(right[j]);
        j++;
    }
    
    return result;
}

// 示例
const arr = [8, 3, 1, 7, 0, 10, 2];
console.log(mergeSort(arr)); // 输出: [0, 1, 2, 3, 7, 8, 10]

时间复杂度分析：

拆分过程：将数组递归拆分为 2ⁿ 个子数组，需要 log₂n 层递归，即 O (log n)。
合并过程：每一层的合并操作总耗时为 O (n)（所有子数组的元素总数为 n）。
总时间复杂度：O (n log n)（每层 O (n) × log n 层）。

总结

O (log n)：常见于「二分查找」「平衡二叉树操作」等，每步将问题规模减半。
O (n log n)：常见于「归并排序」「快速排序（平均情况）」「堆排序」等，结合了线性遍历和对数级拆分。