数学建模 —— 数学规划模型（5）

一、数学规划

**数学规划(Mathematical Programming)**是应用数学的一个重要分支，并非指某种特定的面向数学的计算机编程技术。

该术语由哈佛大学的Robert Dorfman****最先使用，其初始含义具有相当的包容性，从数学的角度表达了人们处理实际问题的一种理念。如下图所示：

五步法建模：

1.1 数学规划问题一般形式

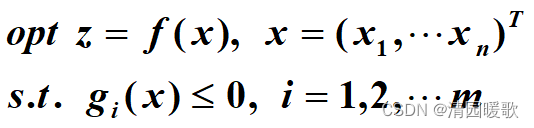
满足约束条件的解叫做可行解，由所有可行解组成的集合叫做可行域。

于是数学规划问题可以表述为：求满足约束条件的*x****，使f(x*)成为最优（最小或最大值），而将x*称为数学规划问题的最优解，将f*=f(x*)称为最优值****。相当于高等数学里的条件极值。**

数学规划的研究对象是数值最优化问题，所以，数学规划现在被通俗的称为最优化(optimization)****。

二、常见规划模型

2.1 线性规划（Linear Programming）

2.1.1 定义

数学规划模型中，如果

（1）目标函数为决策变量的线性函数；

（2）约束条件为决策变量的线性等式或线性不等式，

则称之为线性规划(Linear programming,记为LP）。

2.1.2 一般形式

目标函数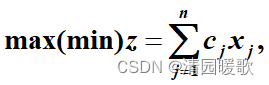

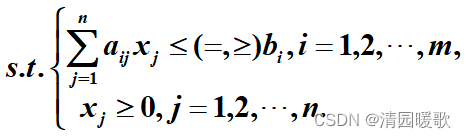
2.1.3 标准形式

目标函数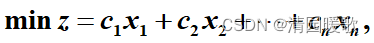

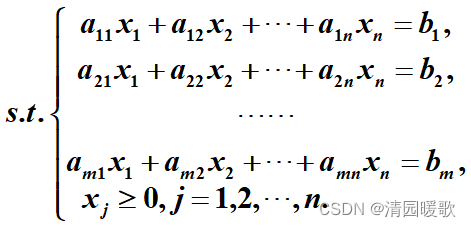
或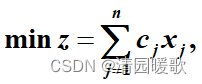

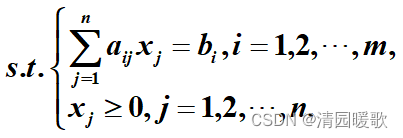
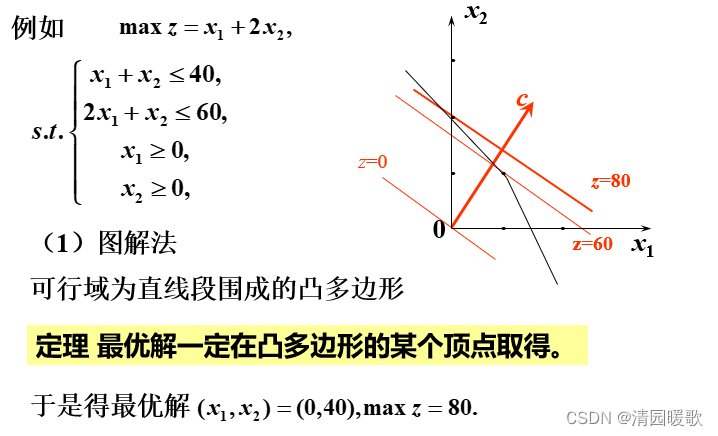
2.1.4 求解

2.2 整数规划（Integer Programming）

2.2.1 单目标规划

定义**：数学规划中的变量****(部分或全部)限制为整数时，称为整数规划。缩写IP****。**

若在线性规划中，变量限制为整数，则称为整数线性规划。若无特别说明，整数规划一般指整数线性规划**。**

若整数规划中某个变量仅取0和1，则称为 0-1型整数规划。

分类**：变量全部限制为整数时，称为纯****(完全)**整数规划。

变量部分限制为整数时，称为混合整数规划。

特点**：**

（1）原线性规划有最优解，当变量限制为整数后，整数规划解的可能情况：

①原线性规划的最优解全为整数，则整数规划的最优解不变；

②整数规划无可行解；

③有可行解（当然就存在最优解），但最优解值变差。

**（2）**整数规划最优解不能按实数最优解简单取整而获得。

2.2.2 两目标规划

若进行加权形成一个目标：

2.3 非线性规划（Nonlinear Programming）

2.3.1 定义

定义：如果线性规划的目标函数或约束函数中含非线性函数，则称之为非线性规划。

注意**：**

**（1）**线性规划与非线性规划区别，若线性规划的最优解存在，则只能在可行域的边界特别是顶点达到，而非线性规划则可能在可行域的任意一点达到；

**（2）**非线性规划目前没有一般的算法，各方法都有特定的适用范围，解非线性规划问题比解线性规划问题困难很多。

2.3.2 灵敏性及稳健性分析

（1）灵敏性

数学建模的整个过程从一些假设开始，但我们很少能保证这些假设是完全正确的，因此需要考虑所得结果对每一条假设的敏感程度。

（2）稳健性

一个数学模型称为稳健的，是指即使模型不完全精确，由其导出的结论也是可靠的。

2.3.3 求解

（1）无约束条件最优解：多元函数求极值；

有约束条件最优解：条件极值，拉格朗日乘数法

（2）计算软件

用Matlab工具箱求解非线性规划问题（略）

三、注意

1**、**尽量使用实数优化，减少整数约束和整数变量

2**、**尽量使用光滑优化，减少非光滑约束的个数

如：尽量少使用绝对值、符号函数、多个变量求最大**/**最小

值、四舍五入、取整函数等

3**、**尽量使用线性模型，减少非线性约束和非线性变量的个数

（如x/y**<5****改为x<5y）**

4**、**合理设定变量上下界，尽可能给出变量初始值

5**、模型中使用的参数数量级要适当(如小于103)**