半导体光子电学期末笔记1: 电磁光学基本理论

Chapter 2: 电磁光学基本理论

电磁光学理论概述

真空中麦克斯韦方程组[p9]

在自由空间中，麦克斯韦方程组可以写成如下形式：

{ ∇ × H = ϵ 0 ∂ E ∂ t (1) ∇ × E = − μ 0 ∂ H ∂ t (2) ∇ ⋅ E = 0 (3) ∇ ⋅ H = 0 (4) \begin{cases} \nabla \times \mathbf{H} = \epsilon_0 \frac{\partial \mathbf{E}}{\partial t} & \text{(1)} \\ \nabla \times \mathbf{E} = -\mu_0 \frac{\partial \mathbf{H}}{\partial t} & \text{(2)} \\ \nabla \cdot \mathbf{E} = 0 & \text{(3)} \\ \nabla \cdot \mathbf{H} = 0 & \text{(4)} \end{cases} ⎩ ⎨ ⎧∇×H=ϵ0∂t∂E∇×E=−μ0∂t∂H∇⋅E=0∇⋅H=0(1)(2)(3)(4)

其中， ϵ 0 \epsilon_0 ϵ0 是自由空间的电容率， μ 0 \mu_0 μ0 是自由空间的磁导率。
意义：

麦克斯韦方程组通过这四个方程完整地描述了电磁场的动态行为：

法拉第电磁感应定律（变化的磁场产生旋转的电场）。
安培环路定律（麦克斯韦修正）（变化的电场产生旋转的磁场）。
高斯定律（电场）（电场的源是电荷）。
高斯定律（磁场）（磁场线总是闭合的）。

波动方程的推导（P5）

首先，对方程 (1) 取旋度：

∇ × ( ∇ × H ) = ∇ × ( ϵ 0 ∂ E ∂ t ) \nabla \times (\nabla \times \mathbf{H}) = \nabla \times \left( \epsilon_0 \frac{\partial \mathbf{E}}{\partial t} \right) ∇×(∇×H)=∇×(ϵ0∂t∂E)

利用矢量分析中的公式 (\nabla \times (\nabla \times \mathbf{A}) = \nabla (\nabla \cdot \mathbf{A}) - \nabla^2 \mathbf{A})，并结合方程 (3)，有：

∇ × ( ∇ × H ) = − ∇ 2 H \nabla \times (\nabla \times \mathbf{H}) = -\nabla^2 \mathbf{H} ∇×(∇×H)=−∇2H

因此，原方程变为：

− ∇ 2 H = ϵ 0 ∂ ∂ t ( ∇ × E ) -\nabla^2 \mathbf{H} = \epsilon_0 \frac{\partial}{\partial t} (\nabla \times \mathbf{E}) −∇2H=ϵ0∂t∂(∇×E)

再利用方程 (2)，代入得到：

∇ 2 H = μ 0 ϵ 0 ∂ 2 H ∂ t 2 \nabla^2 \mathbf{H} = \mu_0 \epsilon_0 \frac{\partial^2 \mathbf{H}}{\partial t^2} ∇2H=μ0ϵ0∂t2∂2H

类似地，对方程 (2) 取旋度：

∇ × ( ∇ × E ) = − ∇ × ( μ 0 ∂ H ∂ t ) \nabla \times (\nabla \times \mathbf{E}) = -\nabla \times \left( \mu_0 \frac{\partial \mathbf{H}}{\partial t} \right) ∇×(∇×E)=−∇×(μ0∂t∂H)

同样利用矢量分析公式和方程 (4)，得到：

∇ 2 E = μ 0 ϵ 0 ∂ 2 E ∂ t 2 \nabla^2 \mathbf{E} = \mu_0 \epsilon_0 \frac{\partial^2 \mathbf{E}}{\partial t^2} ∇2E=μ0ϵ0∂t2∂2E

这两个方程即为自由空间中的电磁波动方程：

{ ∇ 2 E − μ 0 ϵ 0 ∂ 2 E ∂ t 2 = 0 ∇ 2 H − μ 0 ϵ 0 ∂ 2 H ∂ t 2 = 0 \begin{cases} \nabla^2 \mathbf{E} - \mu_0 \epsilon_0 \frac{\partial^2 \mathbf{E}}{\partial t^2} = 0 \\ \nabla^2 \mathbf{H} - \mu_0 \epsilon_0 \frac{\partial^2 \mathbf{H}}{\partial t^2} = 0 \end{cases} {∇2E−μ0ϵ0∂t2∂2E=0∇2H−μ0ϵ0∂t2∂2H=0

波动方程中的系数 (\mu_0 \epsilon_0) 与光速 (c) 的关系如下：

c = 1 μ 0 ϵ 0 c = \frac{1}{\sqrt{\mu_0 \epsilon_0}} c=μ0ϵ0 1

电磁波动方程可以简化为标量波动方程，如图所示：

∇ 2 u − 1 c 2 ∂ 2 u ∂ t 2 = 0 \nabla^2 u - \frac{1}{c^2} \frac{\partial^2 u}{\partial t^2} = 0 ∇2u−c21∂t2∂2u=0

通过解这个方程，可以得到波在介质中的传播速度、方向和波形。这个方程描述了波在自由空间中的传播特性，并遵循线性方程的叠加原理。

无源介质中的麦克斯韦方程组（P6)

在没有自由电荷和电流的介质中，除了电场 E ( r , t ) \mathbf{E}(r, t) E(r,t)和磁场 H ( r , t ) \mathbf{H}(r, t) H(r,t) 之外，还需要引入两个附加的矢量场：

电位移矢量 D ( r , t ) \mathbf{D}(r, t) D(r,t)：描述电场在介质中的表现。
磁感应强度 B ( r , t ) \mathbf{B}(r, t) B(r,t)：描述磁场在介质中的表现。

D = ϵ 0 E + P \mathbf{D} = \epsilon_0 \mathbf{E} + \mathbf{P} D=ϵ0E+P

B = μ 0 H + μ 0 M \mathbf{B} = \mu_0 \mathbf{H} + \mu_0 \mathbf{M} B=μ0H+μ0M

极化密度 P \mathbf{P} P：描述电场作用下，介质中电偶极子的排列情况。它反映了介质对外加电场的响应。
磁化密度 M \mathbf{M} M：描述磁场作用下，介质中磁偶极子的排列情况。它反映了介质对外加磁场的响应。

在没有自由电荷和电流的介质中，麦克斯韦方程组的形式为：

{ ∇ × H = ∂ D ∂ t (1) ∇ × E = − ∂ B ∂ t (2) ∇ ⋅ D = 0 (3) ∇ ⋅ B = 0 (4) \begin{cases} \nabla \times \mathbf{H} = \frac{\partial \mathbf{D}}{\partial t} & \text{(1)} \\ \nabla \times \mathbf{E} = -\frac{\partial \mathbf{B}}{\partial t} & \text{(2)} \\ \nabla \cdot \mathbf{D} = 0 & \text{(3)} \\ \nabla \cdot \mathbf{B} = 0 & \text{(4)} \end{cases} ⎩ ⎨ ⎧∇×H=∂t∂D∇×E=−∂t∂B∇⋅D=0∇⋅B=0(1)(2)(3)(4)

这些关系说明了介质的电磁特性如何通过极化和磁化影响电磁场的传播.

边界条件（Boundary Conditions）(P7)

连续性条件 ：在两个介电介质的交界面上，连续性条件保证了电磁场在过渡时的平滑性和物理合理性。这些条件来源于麦克斯韦方程组，并确保电磁波能够在不同介质中无反射或无畸变地传播。
图 (a) ：在两个介电介质的交界面上，电场 E \mathbf{E} E、磁场 H \mathbf{H} H、电位移矢量 D \mathbf{D} D 和磁感应强度 B \mathbf{B} B 的表现。其中， E \mathbf{E} E 和 H \mathbf{H} H 的切向分量连续， D \mathbf{D} D和 B \mathbf{B} B 的法向分量连续。
切向电场为零 ：在介电介质与理想导体的交界面上，切向电场为零的条件反映了理想导体内部的电场为零的性质。这对于理解导体在电磁波传播中的屏蔽效应和反射特性非常重要。
图 (b)：在介电介质和理想导体的交界面上，电场的切向分量必须为零，这表明在理想导体表面没有切向电场，确保电场线垂直于导体表面。

电磁波在不同介质交界面上的边界条件。

强度、功率与能量:坡印廷定理（Poynting Theorem）[P8]

1. 坡印廷矢量（Poynting Vector）

坡印廷矢量 S \mathbf{S} S 描述了电磁波的能量流密度 ，表示电磁能量在空间中的流动方向和强度。方向为电磁能量传播的方向，其大小表示单位时间内通过单位面积的能量。其定义为：
S = E × H \mathbf{S} = \mathbf{E} \times \mathbf{H} S=E×H
∇ ⋅ S = − ∂ W ∂ t \nabla \cdot \mathbf{S} = -\frac{\partial \mathcal{W}}{\partial t} ∇⋅S=−∂t∂W

能量密度 W \mathcal{W} W 表示为：
W = 1 2 ϵ E 2 + 1 2 μ H 2 \mathcal{W} = \frac{1}{2} \epsilon \mathbf{E}^2 + \frac{1}{2} \mu \mathbf{H}^2 W=21ϵE2+21μH2
2. 光强度（Optical Intensity）

光强度 I ( r , t ) I(r, t) I(r,t) 是时间平均的坡印廷矢量的大小，单位为 W / m 2 \text{W}/\text{m}^2 W/m2。光强度描述了电磁波在单位面积上的能量流动速率。
I ( r , t ) = ⟨ S ⟩ I(r, t) = \langle \mathbf{S} \rangle I(r,t)=⟨S⟩

时间平均的坡印廷矢量 ⟨ S ⟩ \langle \mathbf{S} \rangle ⟨S⟩ 表示在一个周期内坡印廷矢量的平均值。

3. 坡印廷定理（Poynting Theorem）

坡印廷定理是能量守恒定律在电磁场中的体现。它描述了电磁场中能量的变化、传输和消耗。定理的数学表达式为：
∇ ⋅ S = − ∂ ∂ t ( 1 2 ϵ 0 E 2 + 1 2 μ 0 H 2 ) − E ⋅ ∂ P ∂ t − μ 0 H ⋅ ∂ M ∂ t \nabla \cdot \mathbf{S} = -\frac{\partial}{\partial t} \left( \frac{1}{2} \epsilon_0 \mathbf{E}^2 + \frac{1}{2} \mu_0 \mathbf{H}^2 \right) - \mathbf{E} \cdot \frac{\partial \mathbf{P}}{\partial t} - \mu_0 \mathbf{H} \cdot \frac{\partial \mathbf{M}}{\partial t} ∇⋅S=−∂t∂(21ϵ0E2+21μ0H2)−E⋅∂t∂P−μ0H⋅∂t∂M

坡印廷定理反映了电磁场中的能量守恒。它说明了电磁能量的三个主要方面：

能量的流动: ∇ ⋅ S \nabla \cdot \mathbf{S} ∇⋅S 表示单位体积内能量流的净流出量。
能量的存储: ∂ ∂ t ( 1 2 ϵ 0 E 2 + 1 2 μ 0 H 2 ) \frac{\partial}{\partial t} \left( \frac{1}{2} \epsilon_0 \mathbf{E}^2 + \frac{1}{2} \mu_0 \mathbf{H}^2 \right) ∂t∂(21ϵ0E2+21μ0H2) 表示电磁波中的能量密度随时间的变化，其中 1 2 ϵ 0 E 2 \frac{1}{2} \epsilon_0 \mathbf{E}^2 21ϵ0E2 是电场的能量密度， 1 2 μ 0 H 2 \frac{1}{2} \mu_0 \mathbf{H}^2 21μ0H2 是磁场的能量密度。
能量的消耗（通过介质的极化和磁化作用）。 E ⋅ ∂ P ∂ t + μ 0 H ⋅ ∂ M ∂ t \mathbf{E} \cdot \frac{\partial \mathbf{P}}{\partial t} + \mu_0 \mathbf{H} \cdot \frac{\partial \mathbf{M}}{\partial t} E⋅∂t∂P+μ0H⋅∂t∂M.这部分表示电磁场与介质相互作用过程中功率的消耗或存储。

电磁波在介电介质中的传播

先介绍线性、非色散、均匀和各向同性介质中的传播的basic版本，后介绍非均匀，各向异，非线性介质对极化密度P的影响，从而导致其他性质的变化。

线性、非色散、均匀和各向同性介质中的传播 [p10]

其他所有形式的basic版本。

1. 极化密度与电场的关系:
P = ϵ 0 χ E \mathbf{P} = \epsilon_0 \chi \mathbf{E} P=ϵ0χE

线性关系，电极化率 χ \chi χ：介质对电场响应的程度。
2. 电位移矢量与电场的关系:
D = ϵ E \mathbf{D} = \epsilon \mathbf{E} D=ϵE

电容率 ϵ \epsilon ϵ：介质的电容率，定义为 ϵ = ϵ 0 ( 1 + χ ) \epsilon = \epsilon_0 (1 + \chi) ϵ=ϵ0(1+χ)。
3. 麦克斯韦方程组:

此时麦克斯韦方程组可以写成以下形式：
{ ∇ × H = ϵ ∂ E ∂ t (1) ∇ × E = − μ ∂ H ∂ t (2) ∇ ⋅ E = 0 (3) ∇ ⋅ H = 0 (4) \begin{cases} \nabla \times \mathbf{H} = \epsilon \frac{\partial \mathbf{E}}{\partial t} & \text{(1)} \\ \mathbf{\nabla} \times \mathbf{E} = -\mu \frac{\partial \mathbf{H}}{\partial t} & \text{(2)} \\ \nabla \cdot \mathbf{E} = 0 & \text{(3)} \\ \nabla \cdot \mathbf{H} = 0 & \text{(4)} \end{cases} ⎩ ⎨ ⎧∇×H=ϵ∂t∂E∇×E=−μ∂t∂H∇⋅E=0∇⋅H=0(1)(2)(3)(4)
4. 在介质中的波速:

通过麦克斯韦方程组，可以推导出电磁波在介质中的波动方程：
∇ 2 u − 1 c 2 ∂ 2 u ∂ t 2 = 0 \nabla^2 u - \frac{1}{c^2} \frac{\partial^2 u}{\partial t^2} = 0 ∇2u−c21∂t2∂2u=0描述电磁波在介质中的传播特性。从而推导出波速，与介质的电容率和磁导率有关，定义为 c = 1 ϵ μ c = \frac{1}{\sqrt{\epsilon \mu}} c=ϵμ 1。

5. 折射率

介质的折射率 n n n 定义为电磁波在真空中的速度与在介质中的速度之比：
n = c 0 c = ϵ μ ϵ 0 μ 0 n = \frac{c_0}{c} = \sqrt{\frac{\epsilon \mu}{\epsilon_0 \mu_0}} n=cc0=ϵ0μ0ϵμ

非均匀介质（inhomogeneous media）中的传播特性 [P11]

在均匀介质中，极化密度 P \mathbf{P} P 和电场 E \mathbf{E} E 的关系与位置 r r r 无关。这意味着介质在所有位置具有相同的电学特性。

在非均匀介质中，电极化率 χ \chi χ:
χ = χ ( r ) \chi = \chi(r) χ=χ(r)

从而使 P \mathbf{P} P也成为与位置相关的矢量。

从而含有这些变量的相关方程的性质也会随位置变化

扰动理论（Perturbation Theory）

n = n 0 + Δ n n = n_0 + \Delta n n=n0+Δn这种假设表明折射率 n n n 可以看作一个基准值 n 0 n_0 n0 加上一个小的扰动 Δ n \Delta n Δn。

各向异性介质（Anisotropic Media）[P12]

在各向异性介质中，极化密度 KaTeX parse error: Unexpected end of input in a macro argument, expected '}' at end of input: \mathbf{P 依赖于电场矢量 E \mathbf{E} E 的方向。这与各向同性介质不同，在各向同性介质中，极化密度与电场的关系与方向无关。
P i = ϵ 0 ∑ j χ i j E j P_i = \epsilon_0 \sum_j \chi_{ij} E_j Pi=ϵ0j∑χijEj
D i = ∑ j ϵ i j E j D_i = \sum_j \epsilon_{ij} E_j Di=j∑ϵijEj
χ i j \chi_{ij} χij 是一个 3 × 3 3 \times 3 3×3 的矩阵，表示电极化率张量。每个元素 χ i j \chi_{ij} χij 描述了电场分量 E j E_j Ej 对极化密度分量 P i P_i Pi 的贡献。 ϵ i j \epsilon_{ij} ϵij同理。

非线性介质（Nonlinear Media）[P13]

在非线性介质中，极化密度 P \mathbf{P} P 与电场 E \mathbf{E} E之间存在非线性关系。通常表示为：
P = Ψ ( E ) \mathbf{P} = \Psi(\mathbf{E}) P=Ψ(E)

Elementary EM waves

单色电磁波（Monochromatic EM Waves）(频域分析）[P14]

单色电磁波是指频率固定的谐波电磁波，其电场和磁场均为时间的简谐函数。
1. 单色电磁波的定义

单色电磁波的电场 E ( r , t ) \mathbf{E}(r, t) E(r,t) 和磁场 H ( r , t ) \mathbf{H}(r, t) H(r,t) 可以表示为时间的谐波函数，其形式为： E ( r , t ) = Re { E ( r ) exp ⁡ ( j ω t ) } \mathbf{E}(r, t) = \text{Re} \{ \mathbf{E}(r) \exp(j \omega t) \} E(r,t)=Re{E(r)exp(jωt)} H ( r , t ) = Re { H ( r ) exp ⁡ ( j ω t ) } \mathbf{H}(r, t) = \text{Re} \{ \mathbf{H}(r) \exp(j \omega t) \} H(r,t)=Re{H(r)exp(jωt)}

E ( r ) \mathbf{E}(r) E(r) 和 H ( r ) \mathbf{H}(r) H(r)：表示空间位置 r r r 处的电场和磁场的复振幅。

2. 单色电磁波的麦克斯韦方程组

对于单色电磁波，麦克斯韦方程组可以简化为： ∇ × H = j ω D \nabla \times \mathbf{H} = j \omega \mathbf{D} ∇×H=jωD ∇ × E = − j ω B \nabla \times \mathbf{E} = -j \omega \mathbf{B} ∇×E=−jωB ∇ ⋅ D = 0 \nabla \cdot \mathbf{D} = 0 ∇⋅D=0 ∇ ⋅ B = 0 \nabla \cdot \mathbf{B} = 0 ∇⋅B=0

3. 复坡印廷矢量（Complex Poynting Vector）

复坡印廷矢量用于描述电磁波的能量流密度，其定义为： S = 1 2 E × H ∗ \mathbf{S} = \frac{1}{2} \mathbf{E} \times \mathbf{H}^* S=21E×H∗

解释：

S \mathbf{S} S：复坡印廷矢量。
E \mathbf{E} E：电场矢量。
H ∗ \mathbf{H}^* H∗：磁场矢量的复共轭。

4. 光强度（Optical Intensity）

光强度是时间平均的坡印廷矢量的大小，描述了电磁波在单位面积上的能量流动速率。光强度的计算公式为：

⟨ S ⟩ = 1 4 ( E × H ∗ + E ∗ × H ) = 1 2 ( S + S ∗ ) = Re { S } \langle \mathbf{S} \rangle = \frac{1}{4} (\mathbf{E} \times \mathbf{H}^* + \mathbf{E}^* \times \mathbf{H}) = \frac{1}{2} (\mathbf{S} + \mathbf{S}^*) = \text{Re} \{ \mathbf{S} \} ⟨S⟩=41(E×H∗+E∗×H)=21(S+S∗)=Re{S}

公式中的 1 4 \frac{1}{4} 41 和 1 2 \frac{1}{2} 21 是归一化因子，确保计算出的光强度是平均值。

平面电磁波[P15-16]

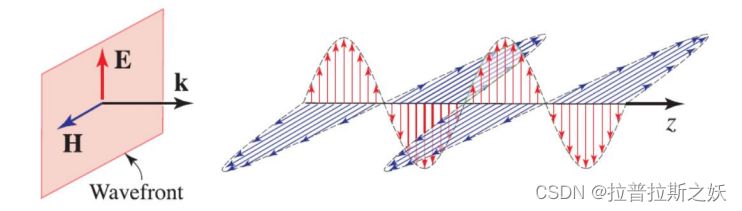
平面电磁波解 ：通过亥姆霍兹方程，对于单色平面电磁波，电场和磁场可以分别表示为：
H ( r ) = H 0 exp ⁡ ( − j k ⋅ r ) E ( r ) = E 0 exp ⁡ ( − j k ⋅ r ) \mathbf{H}(\mathbf{r}) = \mathbf{H}_0 \exp(-j\mathbf{k} \cdot \mathbf{r})\\ \mathbf{E}(\mathbf{r}) = \mathbf{E}_0 \exp(-j\mathbf{k} \cdot \mathbf{r}) H(r)=H0exp(−jk⋅r)E(r)=E0exp(−jk⋅r)

这里， H 0 \mathbf{H}_0 H0 和 E 0 \mathbf{E}_0 E0 是磁场和电场的复数振幅， k \mathbf{k} k 是波矢量， r \mathbf{r} r 是位置矢量， j j j 是虚数单位。这些表达式描述了电磁波在空间中的传播特性。
电磁波的关系式 ：电场和磁场之间的关系式：
k × H 0 = − ω ϵ E 0 k × E 0 = ω μ H 0 \mathbf{k} \times \mathbf{H}_0 = -\omega \epsilon \mathbf{E}_0 \\ \mathbf{k} \times \mathbf{E}_0 = \omega \mu \mathbf{H}_0 k×H0=−ωϵE0k×E0=ωμH0

这些关系式表明，在平面电磁波中，电场和磁场是相互垂直的，并且它们的振动方向也与波的传播方向垂直。这种波被称为横电磁波（Transverse Electromagnetic Wave, TEM）。(如图所示）
介质阻抗和波阻抗 ：介质的阻抗（Impedance）：
η = E 0 H 0 = μ ϵ \eta = \frac{E_0}{H_0} = \sqrt{\frac{\mu}{\epsilon}} η=H0E0=ϵμ

对于非磁性介质（ μ = μ 0 \mu = \mu_0 μ=μ0），阻抗简化为：
η = μ 0 ϵ \eta = \sqrt{\frac{\mu_0}{\epsilon}} η=ϵμ0

在真空中，这个阻抗值为：
η 0 = μ 0 ϵ 0 ≈ 120 π ≈ 377 Ω \eta_0 = \sqrt{\frac{\mu_0}{\epsilon_0}} \approx 120\pi \approx 377 \Omega η0=ϵ0μ0 ≈120π≈377Ω
能量流密度和强度 ：坡印廷矢量（Poynting Vector）描述了电磁波的能量流密度，其方向与波矢量 (\mathbf{k}) 平行：
S = 1 2 E × H ∗ \mathbf{S} = \frac{1}{2} \mathbf{E} \times \mathbf{H}^* S=21E×H∗

这里， H ∗ \mathbf{H}^* H∗ 表示磁场的共轭复数。电磁波的强度（Intensity）可以通过坡印廷矢量计算：
I = ∣ E 0 ∣ 2 2 η I = \frac{|E_0|^2}{2\eta} I=2η∣E0∣2

电偶极子辐射的球面波 Dipole (Spherical wave)

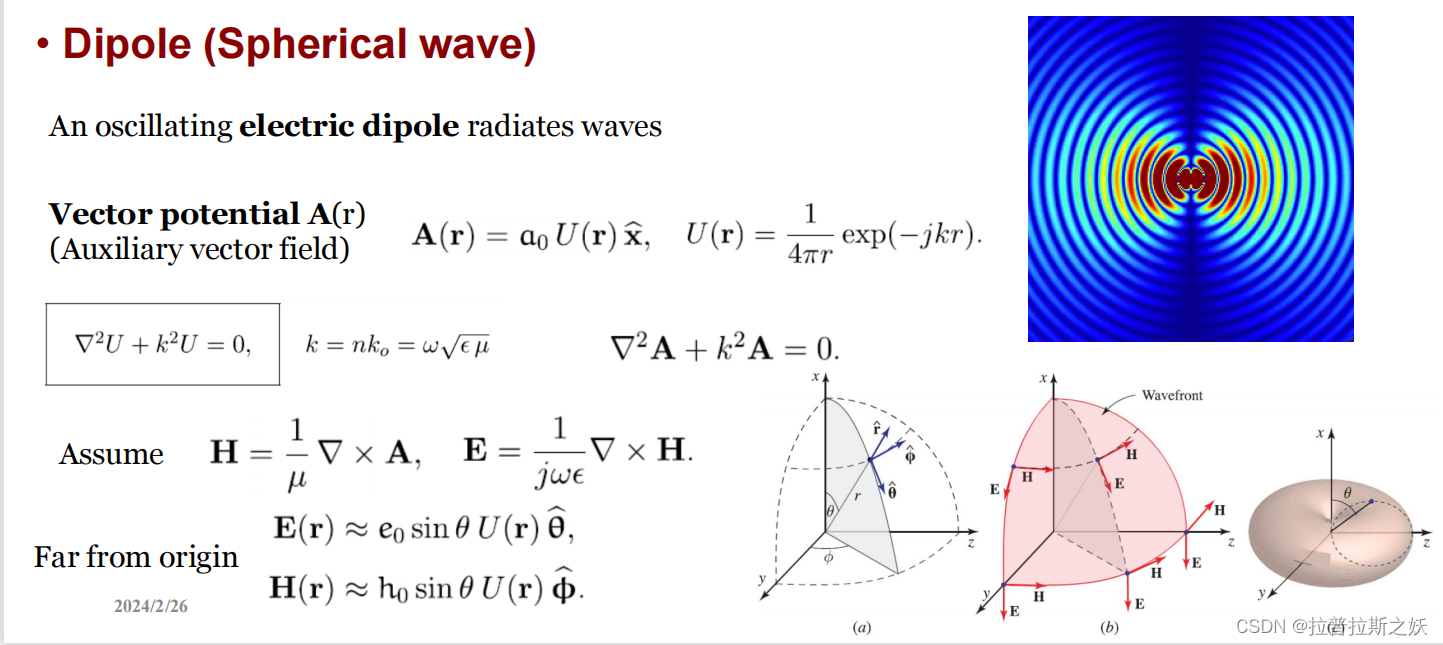
电偶极子是两个电荷大小相等、符号相反且距离很近的点电荷系统。当电偶极子振荡时，它会辐射电磁波。与平面波不同，这是球面波，但同样有电场和磁场垂直的特性。

在远离电偶极子（远场）时，电场和磁场的表达式可以近似为：
E ( r ) ≈ e 0 sin ⁡ θ U ( r ) θ ^ H ( r ) ≈ h 0 sin ⁡ θ U ( r ) ϕ ^ \mathbf{E(r)} \approx e_0 \sin \theta \, U(r) \, \hat{\theta} \\ \mathbf{H(r)} \approx h_0 \sin \theta \, U(r) \, \hat{\phi} E(r)≈e0sinθU(r)θ^H(r)≈h0sinθU(r)ϕ^

这意味着，在远场区域，电场和磁场主要分布在垂直于辐射方向的平面上，并且它们的幅度与距离的平方成反比。

矢量光束（Vector Beams）[P18]

矢量光束是光学领域中一种特殊的光束，它的电场矢量方向在空间上是不均匀的。这种非均匀性使得矢量光束在许多应用中表现出独特的性质。

方位角极化（Azimuthal Polarization）：

在这种极化形式下，电场矢量沿着方位角方向分布。图(a)显示了这种极化形式，电场矢量（E）沿着环形的方位角方向排列。这种极化的光束在横截面上形成一个圆环状的极化模式。

径向极化（Radial Polarization）：

在这种极化形式下，电场矢量沿径向方向分布。图(b)显示了径向极化形式，电场矢量从中心向外沿径向方向排列。这种极化形式使得光束在焦点附近能够聚焦到一个非常小的点，这对于高分辨率显微镜技术特别有用。

Absorption and dispersion

吸收现象（Absorption）

我们得到了弱吸收材质和强吸收材质的近似折射率和吸收系数表达式

基础概念：

电磁极化率（Electric Susceptibility）: 电磁极化率χ是一个复数，可以表示为：
χ = χ ′ + j χ ′ ′ \chi = \chi' + j\chi'' χ=χ′+jχ′′
其中，χ'是实部，代表介质的电极化能力；χ''是虚部，代表介质的吸收损耗。
波数（Wave Number） : k = ω ϵ μ = k 0 1 + χ = k 0 1 + χ ′ + j χ ′ ′ k = \omega \sqrt{\epsilon \mu} = k_0 \sqrt{1 + \chi} = k_0 \sqrt{1 + \chi' + j\chi''} k=ωϵμ =k01+χ =k01+χ′+jχ′′
波数的分解（Decomposition of Wave Number） :将波数k表示为复数形式可以分解为：
k = β − j 1 2 α k = \beta - j\frac{1}{2}\alpha k=β−j21α
- $ \beta $ 是相位常数（real part of the wave number），描述了波的相位随传播距离 $ z $ 的变化率。
- $ \alpha $ 是吸收系数（imaginary part of the wave number），描述了波的振幅随传播距离 $ z $ 的衰减率。

电磁波的复指数表示与吸收现象

在理想情况下，平面波的表达式为：
A exp ⁡ ( − j k z ) A \exp(-jkz) Aexp(−jkz)

结合波数的复数形式，可以表示为：
A exp ⁡ ( − 1 2 α z ) exp ⁡ ( − j β z ) A \exp\left( -\frac{1}{2}\alpha z \right) \exp(-j\beta z) Aexp(−21αz)exp(−jβz)

这表明平面波在传播过程中不仅存在相位变化（由β决定），还存在幅度衰减（由α决定）。

对于吸收系数α大于零的情况，波的强度会随传播距离衰减。具体表现为：
∣ exp ⁡ ( − 1 2 α z ) ∣ 2 = exp ⁡ ( − α z ) \left| \exp\left( -\frac{1}{2}\alpha z \right) \right|^2 = \exp(-\alpha z) exp(−21αz) 2=exp(−αz)

这说明波的强度I随着传播距离z的增加呈指数衰减，吸收系数α决定了衰减的快慢。

复折射率的表示
β \beta β是传播常数，描述了电磁波相位随距离z的变化率，定义为：
β = n k 0 \beta = nk_0 β=nk0

折射率n可以是复数，其表达式为：
n − j 1 2 α = ϵ ϵ 0 = 1 + χ = 1 + χ ′ + j χ ′ ′ n - j\frac{1}{2}\alpha = \sqrt{\frac{\epsilon}{\epsilon_0}} = \sqrt{1 + \chi} = \sqrt{1 + \chi' + j\chi''} n−j21α=ϵ0ϵ =1+χ =1+χ′+jχ′′

弱吸收介质（Weakly Absorbing Media）

在弱吸收介质中，假设吸收较弱，即 χ ′ ′ ≪ 1 + χ ′ \chi'' \ll 1 + \chi' χ′′≪1+χ′，我们可以对复电磁极化率进行近似处理：
1 + χ ′ + j χ ′ ′ = 1 + χ ′ 1 + j χ ′ ′ 1 + χ ′ ≈ 1 + χ ′ ( 1 + j 1 2 δ ) \sqrt{1 + \chi' + j\chi''} = \sqrt{1 + \chi'}\sqrt{1 + j\frac{\chi''}{1 + \chi'}} \approx \sqrt{1 + \chi'} (1 + j\frac{1}{2}\delta) 1+χ′+jχ′′ =1+χ′ 1+j1+χ′χ′′ ≈1+χ′ (1+j21δ)

其中， δ \delta δ是一个小量。由此可以得到折射率n和吸收系数α的近似表达式：
n ≈ 1 + χ ′ n \approx \sqrt{1 + \chi'} n≈1+χ′
α ≈ k 0 n χ ′ ′ \alpha \approx \frac{k_0}{n} \chi'' α≈nk0χ′′

这表明在弱吸收介质中，折射率主要由 χ ′ \chi' χ′决定，而吸收系数 α \alpha α与 χ ′ ′ \chi'' χ′′成正比。

强吸收介质（Strongly Absorbing Media）

在强吸收介质中，假设吸收很强，即 χ ′ ′ ≫ 1 + χ ′ \chi'' \gg 1 + \chi' χ′′≫1+χ′，我们可以进行不同的近似处理：
1 + χ ′ + j χ ′ ′ ≈ j χ ′ ′ = − j ( − χ ′ ′ ) = ± 1 2 ( 1 − j ) − χ ′ ′ \sqrt{1 + \chi' + j\chi''} \approx \sqrt{j\chi''} = \sqrt{-j(-\chi'')} = \pm \frac{1}{\sqrt{2}}(1 - j)\sqrt{-\chi''} 1+χ′+jχ′′ ≈jχ′′ =−j(−χ′′) =±2 1(1−j)−χ′′

由此可以得到折射率n和吸收系数α的近似表达式：
n ≈ − χ ′ ′ 2 n \approx \frac{\sqrt{-\chi''}}{2} n≈2−χ′′
α ≈ 2 k 0 − χ ′ ′ \alpha \approx 2k_0\sqrt{-\chi''} α≈2k0−χ′′

这表明在强吸收介质中，吸收系数 α \alpha α与 χ ′ ′ \chi'' χ′′的平方根成正比，而折射率与 χ ′ ′ \chi'' χ′′的平方根成正比，但其数值较小。

例题：稀薄吸收介质（Dilute Absorbing Medium）的总体电磁极化率，折射率和吸收系数

题目描述了一个非吸收介质，其折射率为 ( n_0 $，其中悬浮了少量杂质，这些杂质的电磁极化率 ( \chi = \chi' + j\chi'' $ 满足 ( \chi' \ll 1 $ 和 ( \chi'' \ll 1 $。我们需要确定介质的总电磁极化率，并证明折射率和吸收系数的近似表达式如下：
n ≈ n 0 + χ ′ 2 n 0 n \approx n_0 + \frac{\chi'}{2n_0} n≈n0+2n0χ′
α ≈ k 0 χ ′ ′ n 0 \alpha \approx \frac{k_0 \chi''}{n_0} α≈n0k0χ′′

对于一个稀薄吸收介质，我们假设其复折射率可以表示为：
n − j 1 2 α = ϵ ϵ 0 = 1 + χ = 1 + χ ′ + j χ ′ ′ n - j\frac{1}{2}\alpha = \sqrt{\frac{\epsilon}{\epsilon_0}} = \sqrt{1 + \chi} = \sqrt{1 + \chi' + j\chi''} n−j21α=ϵ0ϵ =1+χ =1+χ′+jχ′′

因为 ( \chi' \ll 1 $ 和 ( \chi'' \ll 1 $，我们可以对上述表达式进行近似处理。利用泰勒展开和忽略高阶小量，我们可以得到：
1 + χ ′ + j χ ′ ′ ≈ 1 + χ ′ 1 + j χ ′ ′ 1 + χ ′ \sqrt{1 + \chi' + j\chi''} \approx \sqrt{1 + \chi'} \sqrt{1 + j\frac{\chi''}{1 + \chi'}} 1+χ′+jχ′′ ≈1+χ′ 1+j1+χ′χ′′

进一步简化为：
1 + χ ′ + j χ ′ ′ ≈ 1 + χ ′ ( 1 + j χ ′ ′ 2 ( 1 + χ ′ ) ) \sqrt{1 + \chi' + j\chi''} \approx \sqrt{1 + \chi'} \left(1 + j\frac{\chi''}{2(1 + \chi')}\right) 1+χ′+jχ′′ ≈1+χ′ (1+j2(1+χ′)χ′′)

折射率 ( n $ 可以表示为上述结果的实部部分：
n ≈ 1 + χ ′ ≈ 1 + χ ′ 2 n \approx \sqrt{1 + \chi'} \approx 1 + \frac{\chi'}{2} n≈1+χ′ ≈1+2χ′

但因为介质的本征折射率为 ( n_0 $，我们需要考虑这种基底效应。因此，对于总的折射率 ( n $ 我们有：
n ≈ n 0 + χ ′ 2 n 0 n \approx n_0 + \frac{\chi'}{2n_0} n≈n0+2n0χ′

吸收系数 ( \alpha $ 可以通过虚部部分来表示：
α ≈ 2 k 0 χ ′ ′ 2 ( 1 + χ ′ ) ≈ k 0 χ ′ ′ n 0 \alpha \approx \frac{2k_0 \chi''}{2(1 + \chi')} \approx \frac{k_0 \chi''}{n_0} α≈2(1+χ′)2k0χ′′≈n0k0χ′′

色散

色散是指光波或电磁波在介质中传播时，不同频率的波以不同的速度传播，导致波的各个频率分量发生分离的现象。色散的本质在于介质对不同频率的电磁波有不同的响应。

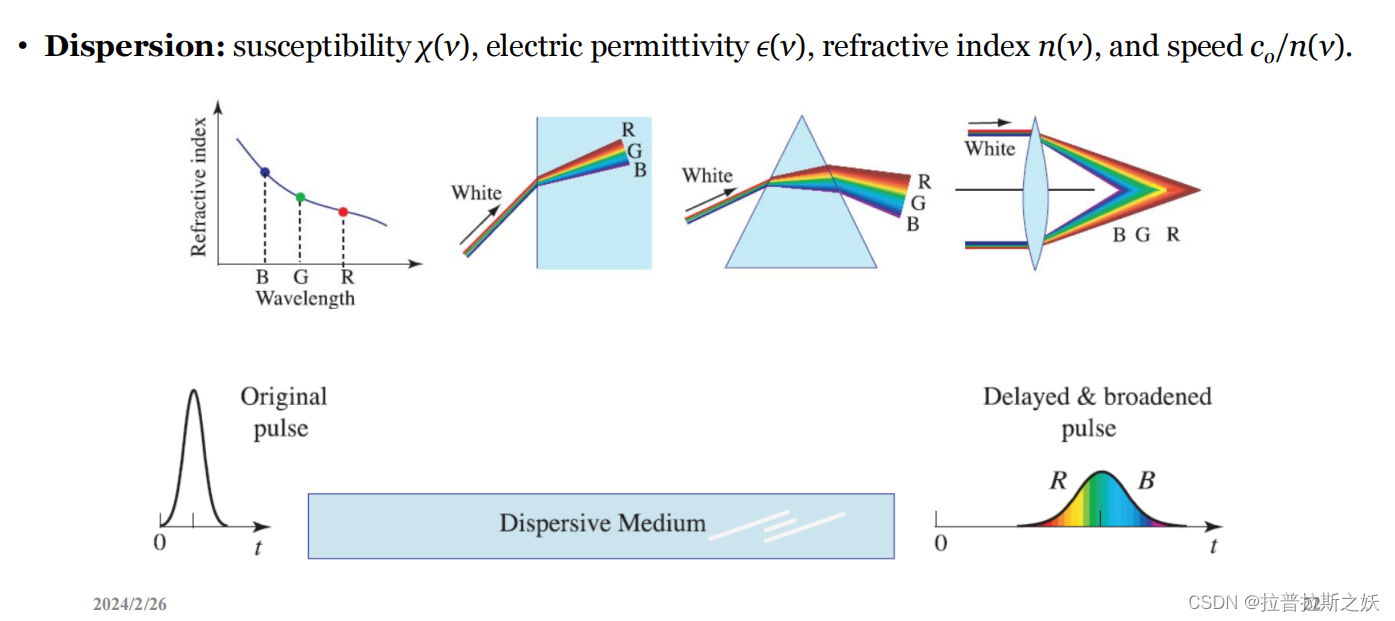
这种响应可以通过以下几个物理量来描述：

电极化率 (χ(ν))：描述介质对电场响应的程度，即电场对介质极化程度的影响。
电容率 (ε(ν))：描述介质对电场的响应能力，它与电极化率直接相关。
折射率 (n(ν))：描述光在介质中的传播速度与真空中光速的比值，折射率的频率依赖性即为色散的直接体现。
相速度 (c₀/n(ν))：光在介质中的传播速度，与折射率成反比。

吸收与色散的关系：克拉莫-克朗尼关系

克拉莫-克朗尼关系从数学上描述了介质的复电极化率（complex susceptibility）的实部和虚部之间的联系。电极化率 (\chi(\nu)) 通常被分解为实部 (\chi'(\nu)) 和虚部 (\chi''(\nu))，其中：

(\chi'(\nu))：描述介质的色散特性，如何影响光的相速度。
(\chi''(\nu))：描述介质的吸收特性，如何吸收光能量。

克拉莫-克朗尼关系的积分形式如下：

[ \chi'(\nu) = \frac{2}{\pi} \int_{0}^{\infty} \frac{s\chi''(s)}{s^2 - \nu^2} , ds ]

[ \chi''(\nu) = \frac{2\nu}{\pi} \int_{0}^{\infty} \frac{\chi'(s)}{\nu^2 - s^2} , ds ]

通过克拉莫-克朗尼关系，可以通过材料在某一频率的吸收特性（虚部）推导出其色散特性（实部），反之亦然。在光谱分析中，材料的吸收光谱可以通过克拉莫-克朗尼关系转换为折射率分布。

吸收与色散在共振频率附近的效果[P24-27]

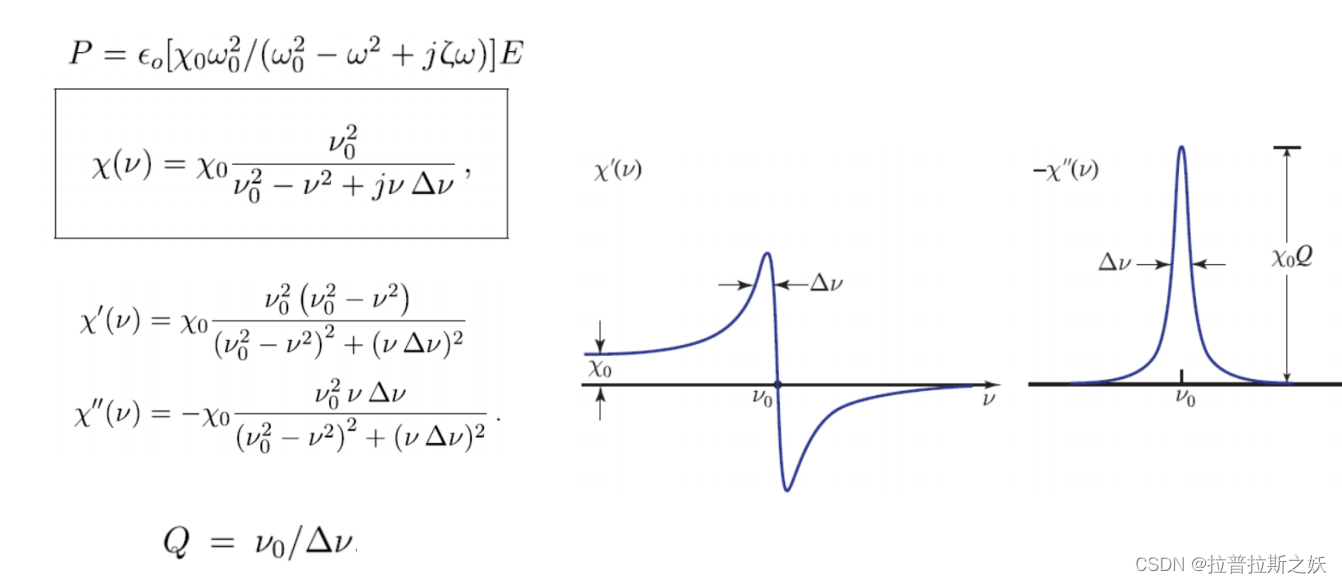
电极化率X（v)分析

洛伦兹振子模型（Lorentz Oscillator Model）的解： χ ( ν ) = χ 0 ν 0 2 ν 0 2 − ν 2 + j ν Δ ν , \chi(\nu)=\chi_0\frac{\nu_0^2}{\nu_0^2-\nu^2+j\nu \Delta\nu} , χ(ν)=χ0ν02−ν2+jνΔνν02,

χ 0 \chi_0 χ0 是静态电极化率；
ν 0 \nu_0 ν0 是共振频率；
Δ ν \Delta\nu Δν 是阻尼系数；
ν \nu ν 是外加电场的频率。

这个表达式描述了在频率为 ν \nu ν 的外加电场作用下，材料的电极化率如何随频率变化。此时，电极化率包含了实部和虚部，分别表示色散和吸收特性。

将电极化率 χ ( ν ) \chi(\nu) χ(ν) 分解为实部 χ ′ ( ν ) \chi'(\nu) χ′(ν) 和虚部 χ ′ ′ ( ν ) \chi''(\nu) χ′′(ν)，可以得到：
χ ′ ( ν ) = χ 0 ν 0 2 ( ν 0 2 − ν 2 ) ( ν 0 2 − ν 2 ) 2 + ( ν Δ ν ) 2 , \chi'(\nu) = \chi_0 \frac{\nu_0^2 (\nu_0^2 - \nu^2)}{(\nu_0^2 - \nu^2)^2 + (\nu \Delta\nu)^2}, χ′(ν)=χ0(ν02−ν2)2+(νΔν)2ν02(ν02−ν2),
χ ′ ′ ( ν ) = − χ 0 ν 0 2 ν Δ ν ( ν 0 2 − ν 2 ) 2 + ( ν Δ ν ) 2 . \chi''(\nu) = -\chi_0 \frac{\nu_0^2 \nu \Delta\nu}{(\nu_0^2 - \nu^2)^2 + (\nu \Delta\nu)^2}. χ′′(ν)=−χ0(ν02−ν2)2+(νΔν)2ν02νΔν.

实部 χ ′ ( ν ) \chi'(\nu) χ′(ν) 描述了介电常数随频率变化的色散特性，而虚部 χ ′ ′ ( ν ) \chi''(\nu) χ′′(ν) 则描述了材料对电磁波的吸收。

右侧的两个图展示了 χ ′ ( ν ) \chi'(\nu) χ′(ν) 和 χ ′ ′ ( ν ) \chi''(\nu) χ′′(ν) 随频率 ν \nu ν 的变化：

χ ′ ( ν ) \chi'(\nu) χ′(ν) 的图像：
- 当 ν = ν 0 \nu = \nu_0 ν=ν0 时，实部 χ ′ ( ν ) \chi'(\nu) χ′(ν) 出现共振峰，随后迅速下降并在 ν 0 \nu_0 ν0 附近出现一个负值的最小值。
- 在远离共振频率 ν 0 \nu_0 ν0 的地方， χ ′ ( ν ) \chi'(\nu) χ′(ν) 接近于零，表明色散效应不明显。
χ ′ ′ ( ν ) \chi''(\nu) χ′′(ν) 的图像：
- 虚部 χ ′ ′ ( ν ) \chi''(\nu) χ′′(ν) 在共振频率 ν 0 \nu_0 ν0 附近达到最大值，随后迅速减小。
- 这一峰值对应于材料的最大吸收率。
- 吸收带宽为 Δ ν \Delta\nu Δν，表示共振吸收的范围。

品质因数 Q Q Q 是衡量共振系统性能的重要参数，定义为：
Q = ν 0 Δ ν . Q = \frac{\nu_0}{\Delta\nu}. Q=Δνν0.

品质因数 Q Q Q 表示共振频率 ν 0 \nu_0 ν0 与吸收带宽 Δ ν \Delta\nu Δν 之比，反映了系统的共振锋利度。较高的 Q Q Q 值表示共振峰较窄，系统具有较高的选择性和较低的能量损耗。

共振附近的行为：
- 左边的表达式和右边的图像展示了 χ ( ν ) \chi(\nu) χ(ν) 在共振频率 ν 0 \nu_0 ν0 附近的行为。
- 实部 χ ′ ( ν ) \chi'(\nu) χ′(ν) 和虚部 χ ′ ′ ( ν ) \chi''(\nu) χ′′(ν) 都显示出在 ν 0 \nu_0 ν0 附近有显著变化，其中 χ ′ ′ ( ν ) \chi''(\nu) χ′′(ν) 在 ν 0 \nu_0 ν0 处有一个尖锐的峰值，表明最大吸收。
- 这种行为可以用来解释材料在特定频率范围内的强吸收和色散效应。
远离共振的行为：
- 右侧的简化公式表明当 ∣ ν − ν 0 ∣ ≫ Δ ν |\nu - \nu_0| \gg \Delta\nu ∣ν−ν0∣≫Δν 时，吸收可以忽略不计，电极化率主要由实部主导，且实部随频率的变化趋于平缓。

吸收系数 (\alpha(\nu))和折射率 (n(\nu))

吸收系数 α ( ν ) \alpha(\nu) α(ν) 描述了电磁波在介质中传播时的衰减程度。其表达式为：
α ( ν ) ≈ − ( 2 π ν n 0 c 0 ) χ ′ ′ ( ν ) \alpha(\nu) \approx -\left(\frac{2\pi\nu}{n_0 c_0}\right) \chi''(\nu) α(ν)≈−(n0c02πν)χ′′(ν)

折射率 n ( ν ) n(\nu) n(ν) 描述了电磁波在介质中传播时的相速度。其表达式为：
n ( ν ) ≈ n 0 + χ ′ ( ν ) 2 n 0 n(\nu) \approx n_0 + \frac{\chi'(\nu)}{2n_0} n(ν)≈n0+2n0χ′(ν)

其中：

n 0 n_0 n0 是介质的本征折射率；
这个表达式表明，折射率是介质本征折射率 n 0 n_0 n0 和电极化率实部的一部分。由于 χ ′ ( ν ) \chi'(\nu) χ′(ν) 在共振频率 ν 0 \nu_0 ν0 附近表现为一个具有明显变化的函数，因此折射率 n ( ν ) n(\nu) n(ν) 也会在共振频率附近发生显著变化。

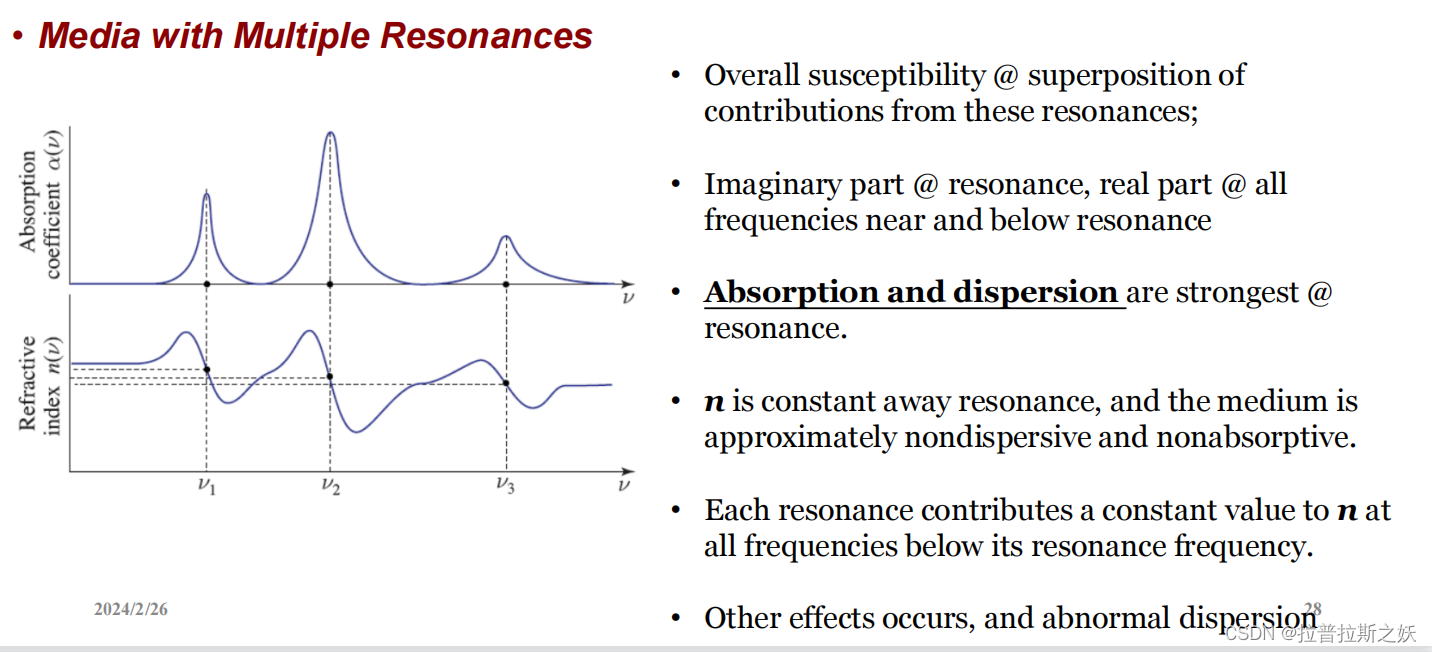
有多个共振频率的介质（Media with Multiple Resonances）[p28]

这一页讨论了具有多个共振频率的介质（Media with Multiple Resonances）的电磁特性。特别是关注在这些共振频率附近的吸收和色散行为。

总的电极化率：
- 总的电极化率是这些共振频率处的贡献的叠加。
- 在每个共振频率处，虚部（吸收）和实部（色散）都显著变化。
虚部和实部：
- 在共振频率处，虚部（吸收）显著。
- 在共振频率附近和以下的所有频率，实部（色散）显著。
吸收和色散最强点：
- 吸收和色散在共振频率处最强。
- 这意味着在这些频率下，介质对电磁波的影响最大。
远离共振频率时的行为：
- 当频率远离共振频率时，折射率 (n) 变得恒定，介质变得几乎无色散和无吸收。
- 这表明在这些频率下，介质对电磁波的影响较小。
各共振的贡献：
- 每个共振在所有低于其共振频率的频率处对折射率 (n) 贡献一个常数值。
- 这意味着在这些频率下，折射率受多个共振频率的影响，表现为多个常数值的叠加。
其他效应和异常色散：
- 由于多个共振频率的存在，还可能出现其他效应和异常色散现象。
- 异常色散通常表现为折射率在某些频率范围内的急剧变化，这在光学和电磁波传播研究中非常重要。

塞尔迈耶方程（Sellmeier Equation）[p29]

这一页介绍了塞尔迈耶方程（Sellmeier Equation），该方程用于描述材料的折射率 𝑛随波长的变化。

Scattering 散射

电磁波的散射现象可以简单理解为当电磁波遇到介质中的不均匀性时，波的传播路径发生改变。这种不均匀性可以是材料的缺陷、颗粒、悬浮粒子等。在一个均匀介质中，这些局部的不均匀性会导致散射波的产生。

Born 近似 [p30]

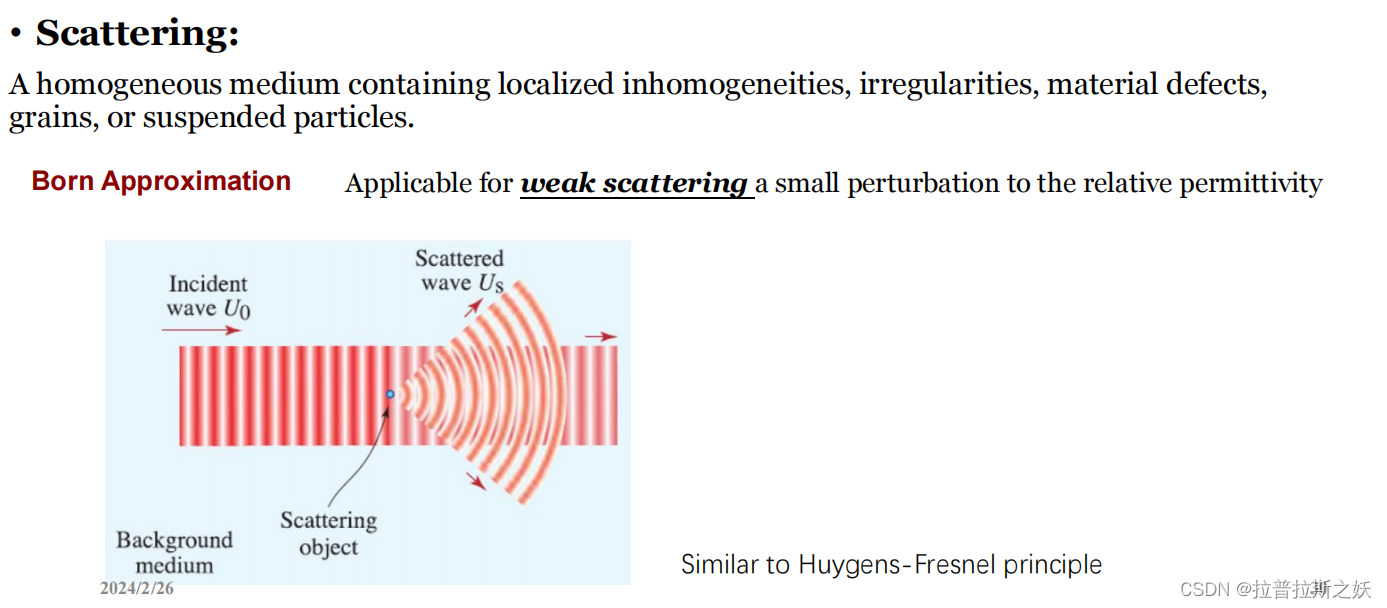
Born 近似是一种用于描述弱散射现象的数学方法。这种方法假设介质的相对**介电常数（permittivity)**只有微小的扰动，即散射非常微弱。这一近似是基于以下假设：

散射的强度较弱。
相对介电常数的变化是一个小扰动。

这种近似方法类似于 Huygens-Fresnel 原理，其中每一个散射点可以被看作是一个次级波源，发出次级波。这些次级波的相干叠加形成了最终的散射波。

图片展示了一个入射波 (U_0) 碰到散射物体后，形成了散射波 (U_s) 的过程。入射波在遇到散射物体时，由于介电常数的变化，导致了波的扰动和散射。这种散射可以用 Born 近似来描述，假设散射强度较弱，即扰动较小。

弱散射情况

在粒子尺寸远小于电磁波波长的条件下，Rayleigh 散射的近似非常有效。这个条件通常适用于气体分子或非常小的悬浮颗粒。例如，大气中的氮气和氧气分子对可见光的散射就是典型的 Rayleigh 散射。

对于弱散射情况，即散射粒子的散射强度较弱时，Born 近似是适用的。这种情况下，可以使用标量波（scalar waves）来描述散射现象。

散射功率公式

页面中的公式给出了总散射功率 P s P_s Ps 的表达式：
P s ≈ 1 6 π ∣ k s 2 − k 2 ∣ 2 V 2 I 0 P_s \approx \frac{1}{6\pi} \left| k_s^2 - k^2 \right|^2 V^2 I_0 Ps≈6π1 ks2−k2 2V2I0

其中：

k s k_s ks 和 k k k 分别是散射波和入射波的波数。
V V V 是散射体的体积。
I 0 I_0 I0 是入射光的强度。

Rayleigh 散射的一个显著特征是散射强度与波长的四次方成反比关系，即：
P s ∝ ω 4 P_s \propto \omega^4 Ps∝ω4

这里的 ω \omega ω 是入射波的角频率。这个关系说明，较短波长的光波（如蓝光）比较长波长的光波（如红光）更容易被散射。这也是为什么天空在白天呈现蓝色，因为大气中的气体分子对短波长的蓝光散射更强烈。

极化的影响

在 Rayleigh 散射中，粒子被认为是偶极子，因此极化效应必须考虑。入射光波会使散射粒子产生偶极子振荡，这些偶极子再发射出散射光波。

图中展示了一个典型的 Rayleigh 散射过程：

入射波 U 0 U_0 U0 遇到散射物体（如一个小粒子）后，粒子作为偶极子开始振荡。
由于偶极子的振荡，产生了散射波，散射波的强度和方向取决于入射波的频率、粒子的大小以及介质的性质。
散射波的强度在各个方向上是不均匀的，这由粒子的形状和极化效应决定。

Scattering cross section 散射截面

散射截面 σ s \sigma_s σs 是描述散射体在电磁波入射时散射能力的一个重要参数。它定义了一个等效的面积，表示这部分面积内截获的入射波能量等于实际散射的能量。

总散射功率 P s P_s Ps 表达为：
P s = σ s I 0 P_s = \sigma_s I_0 Ps=σsI0

其中：

I 0 I_0 I0 是入射光强（单位： W/m 2 \text{W/m}^2 W/m2），
σ s \sigma_s σs 是散射截面（单位： m 2 \text{m}^2 m2）。

这个公式表示，散射功率 P s P_s Ps 等于散射截面乘以入射光的强度。也就是说，散射截面越大，散射的功率就越大

对于一个球形介电散射体，其半径为 a a a，在介电常数为 ϵ \epsilon ϵ 的介质中，其自身的介电常数为 ϵ s \epsilon_s ϵs。散射截面 的公式为：
σ s = π a 2 Q s \sigma_s = \pi a^2 Q_s σs=πa2Qs

其中， Q s Q_s Qs 是散射效率（Scattering Efficiency）。

散射效率 Q s Q_s Qs 的表达式为：
Q s = 8 3 ∣ ϵ s − ϵ ϵ + 2 ϵ ∣ 2 ( 2 π a λ ) 4 Q_s = \frac{8}{3} \left| \frac{\epsilon_s - \epsilon}{\epsilon + 2 \epsilon} \right|^2 \left( \frac{2\pi a}{\lambda} \right)^4 Qs=38 ϵ+2ϵϵs−ϵ 2(λ2πa)4

其中：

ϵ s \epsilon_s ϵs 是散射体的介电常数，
ϵ \epsilon ϵ 是介质的介电常数，
a a a 是散射体的半径，
λ \lambda λ 是入射波的波长。

介电常数的影响：介电常数的差异越大，散射效率越高。这是因为介电常数的差异会导致更强的电场和磁场扰动，从而增强散射。
尺寸效应：散射效率与散射体尺寸的四次方成正比，说明粒子越大，散射越强。这也是为什么在大气中，较大的颗粒（如雾滴）会比小颗粒（如气体分子）产生更明显的散射效应。
波长效应：散射效率与波长的四次方成反比，短波长的光（如蓝光）散射效率更高，这解释了为什么天空在白天呈现蓝色（Rayleigh 散射）。

强散射

在强散射的情况下，介电常数的对比度（ ϵ s − ϵ \epsilon_s - \epsilon ϵs−ϵ）与介质的介电常数 ϵ \epsilon ϵ 的比值并不小。这意味着散射体和周围介质之间的介电常数差异显著，导致散射现象更为强烈。

强散射情况下，散射截面 σ s \sigma_s σs 和散射效率 Q s Q_s Qs 的公式如下：
σ s = π a 2 Q s \sigma_s = \pi a^2 Q_s σs=πa2Qs
Q s = 8 3 ∣ ϵ s − ϵ ϵ s + 2 ϵ ∣ 2 ( 2 π a λ ) 4 Q_s = \frac{8}{3} \left| \frac{\epsilon_s - \epsilon}{\epsilon_s + 2\epsilon} \right|^2 \left( \frac{2\pi a}{\lambda} \right)^4 Qs=38 ϵs+2ϵϵs−ϵ 2(λ2πa)4

其中：

σ s \sigma_s σs 是散射截面，表示一个等效的面积。
a a a 是纳米球的半径。
ϵ s \epsilon_s ϵs 是散射体（纳米球）的介电常数。
ϵ \epsilon ϵ 是介质的介电常数。
λ \lambda λ 是入射波的波长。

散射效率 Q s Q_s Qs 描述了散射强度的效率，强散射情况下，公式中的分母部分 ϵ s + 2 ϵ \epsilon_s + 2\epsilon ϵs+2ϵ 强调了介电常数的对比度对散射效率的影响。

对比弱散射公式：
σ s = π a 2 Q s \sigma_s = \pi a^2 Q_s σs=πa2Qs
Q s = 8 3 ∣ ϵ s − ϵ 3 ϵ ∣ 2 ( 2 π a λ ) 4 Q_s = \frac{8}{3} \left| \frac{\epsilon_s - \epsilon}{3\epsilon} \right|^2 \left( \frac{2\pi a}{\lambda} \right)^4 Qs=38 3ϵϵs−ϵ 2(λ2πa)4

在这种情况下，介电常数的对比度较小，导致分母部分不同，即为 ϵ \epsilon ϵ 的三倍。这种情况通常适用于介电常数差异较小的介质和散射体。

强散射弱散射对比：

介电常数的对比度：在强散射的公式中，介电常数的对比度对散射效率影响更大。这意味着当散射体和介质的介电常数差异显著时，散射效应更为明显。
尺寸和波长效应：无论是强散射还是弱散射，散射效率都与散射体尺寸的四次方和波长的四次方成正比。说明较大的粒子和较短的波长会增强散射效应。

Born 近似、Rayleigh 散射和 Mie 散射对比

Born 近似

Born 近似适用于所有尺寸的弱散射。这种近似假设散射介质中的不均匀性较小，使得散射场可以被视为入射场的一个小扰动。这一假设极大简化了散射问题的数学处理，尤其适用于描述在相对较均匀介质中的微弱散射现象。

Rayleigh 散射

Rayleigh 散射适用于粒子尺寸远小于波长的情况。在这种情况下，散射体可以被视为偶极子，其散射强度与波长的四次方成反比。Rayleigh 散射的重要特点是其散射强度在短波长（如蓝光）时更强，因此解释了为什么天空呈现蓝色，因为大气中的小气体分子对短波长光散射更强。

Mie 散射

Mie 散射描述了与波长相近甚至更大的球形粒子的散射现象。与 Rayleigh 散射不同，Mie 散射不仅仅适用于小粒子，还适用于较大的粒子。在 Mie 散射中，四极子解（quadrupole solutions）对于描述大球体的散射现象非常重要。

基本物理知识

散度与旋度

旋度（Curl, ∇ × \nabla \times ∇×）
旋度是一个向量运算符，用来描述向量场在某点处的旋转性质。对于一个向量场 F = ( F x , F y , F z ) \mathbf{F} = (F_x, F_y, F_z) F=(Fx,Fy,Fz)，其旋度定义为：

∇ × F = ( ∂ F z ∂ y − ∂ F y ∂ z , ∂ F x ∂ z − ∂ F z ∂ x , ∂ F y ∂ x − ∂ F x ∂ y ) \nabla \times \mathbf{F} = \left( \frac{\partial F_z}{\partial y} - \frac{\partial F_y}{\partial z}, \frac{\partial F_x}{\partial z} - \frac{\partial F_z}{\partial x}, \frac{\partial F_y}{\partial x} - \frac{\partial F_x}{\partial y} \right) ∇×F=(∂y∂Fz−∂z∂Fy,∂z∂Fx−∂x∂Fz,∂x∂Fy−∂y∂Fx)

旋度在某点的非零值表示在该点附近存在局部旋转。它的方向给出旋转的轴线，大小表示旋转的强度。

散度（Divergence, ∇ ⋅ \nabla \cdot ∇⋅）

散度是一个标量运算符，用来描述向量场在某点处的发散程度。对于一个向量场 F = ( F x , F y , F z ) \mathbf{F} = (F_x, F_y, F_z) F=(Fx,Fy,Fz)，其散度定义为：

∇ ⋅ F = ∂ F x ∂ x + ∂ F y ∂ y + ∂ F z ∂ z \nabla \cdot \mathbf{F} = \frac{\partial F_x}{\partial x} + \frac{\partial F_y}{\partial y} + \frac{\partial F_z}{\partial z} ∇⋅F=∂x∂Fx+∂y∂Fy+∂z∂Fz

散度的非零值表示在该点有净流出或净流入。比如，在电场中，正电荷是电场线的源（散度为正），负电荷是电场线的汇（散度为负）。

亥姆霍兹方程（Helmholtz equation）

它描述了标量场和矢量场的空间分布，当这些场在时间上以简单谐振荡形式表现时。亥姆霍兹方程通常出现在求解波动方程的时间谐解（steady-state solution）时。

在三维空间中，亥姆霍兹方程的一般形式为：

∇ 2 U + k 2 U = 0 \nabla^2 U + k^2 U = 0 ∇2U+k2U=0

这里， ∇ 2 \nabla^2 ∇2 是拉普拉斯算子， U U U 是标量场（例如压力场、电势场）或矢量场（例如电场、磁场）的一个分量， k k k 是波数，定义为 k = ω c k = \frac{\omega}{c} k=cω，其中 ω \omega ω是角频率， c c c 是波速。

亥姆霍兹方程可以从波动方程中导出。

在电磁学中，亥姆霍兹方程用于描述电磁场在自由空间或介质中的传播。例如，对于一个在均匀、无损耗介质中传播的单色平面电磁波，电场 E \mathbf{E} E 和磁场 H \mathbf{H} H可以分别用亥姆霍兹方程描述：

∇ 2 E + k 2 E = 0 \nabla^2 \mathbf{E} + k^2 \mathbf{E} = 0 ∇2E+k2E=0
∇ 2 H + k 2 H = 0 \nabla^2 \mathbf{H} + k^2 \mathbf{H} = 0 ∇2H+k2H=0

这些方程表示在空间中传播的电磁波的分布。

亥姆霍兹方程的解

亥姆霍兹方程的解形式取决于具体的边界条件和问题的几何配置。在自由空间中，平面波是亥姆霍兹方程的一个基本解，形式为：

Φ ( r ) = Φ 0 exp ⁡ ( j k ⋅ r ) \Phi(\mathbf{r}) = \Phi_0 \exp(j\mathbf{k} \cdot \mathbf{r}) Φ(r)=Φ0exp(jk⋅r)

这里， k \mathbf{k} k 是波矢量，指示波的传播方向和波长。

波数和波矢

波数（Wavenumber）

波数 k k k 通常表示波的空间频率，即波在单位距离内的振荡次数。它是一个标量，定义为：
k = 2 π λ k = \frac{2\pi}{\lambda} k=λ2π

其中 λ \lambda λ 是波长。

波数也可以通过波的传播常数和介质特性来表示。在介质中的波数为：
k = n k 0 k = nk_0 k=nk0

这里 n n n 是介质的折射率，而 k 0 k_0 k0 是在真空中的波数，定义为：
k 0 = ω c k_0 = \frac{\omega}{c} k0=cω

其中 ω \omega ω 是角频率， c c c 是光速。

波矢（Wave Vector）

波矢 k \mathbf{k} k 是一个向量，表示波的传播方向和波数。它不仅包含波的空间频率信息，还包含波传播的方向。波矢的大小等于波数 k k k，其方向与波的传播方向一致。波矢 k \mathbf{k} k 定义为：
k = k e ^ \mathbf{k} = k \hat{e} k=ke^

其中 e ^ \hat{e} e^ 是波的传播方向的单位向量。

波矢的分量可以用来描述波在各个方向上的传播特性。例如，在三维空间中，波矢可以写成：
k = k x i ^ + k y j ^ + k z k ^ \mathbf{k} = k_x \hat{i} + k_y \hat{j} + k_z \hat{k} k=kxi^+kyj^+kzk^

E ( r ) \mathbf{E(r)} E(r) 和 H ( r ) \mathbf{H(r)} H(r)：
- E ( r ) \mathbf{E(r)} E(r) 表示电场强度，单位为伏每米（V/m）。
- H ( r ) \mathbf{H(r)} H(r) 表示磁场强度，单位为安每米（A/m）。
e 0 e_0 e0 和 h 0 h_0 h0：
- e 0 e_0 e0 是电场强度的幅值常数。
- h 0 h_0 h0 是磁场强度的幅值常数。
U ( r ) U(r) U(r)：
- U ( r ) U(r) U(r) 是一个与距离 r r r 相关的标量势场，定义为：
  U ( r ) = 1 4 π r exp ⁡ ( − j k r ) U(r) = \frac{1}{4\pi r} \exp(-jkr) U(r)=4πr1exp(−jkr)
- 这里 r r r 是距离电偶极子的距离，单位为米（m）。
- k k k 是波数，表示波在空间中的传播常数。
- 这个标量场 U ( r ) U(r) U(r) 表示一个球面波的传播特性，包含幅度随距离 r r r 的衰减和相位的变化。
θ ^ \hat{\theta} θ^ 和 ϕ ^ \hat{\phi} ϕ^：
- θ ^ \hat{\theta} θ^ 和 ϕ ^ \hat{\phi} ϕ^ 是单位向量，分别表示在球坐标系中极角方向（ θ \theta θ 方向）和方位角方向（ ϕ \phi ϕ 方向）。

理解公式

电场 E ( r ) \mathbf{E(r)} E(r) 的方向由 θ ^ \hat{\theta} θ^ 决定，表示在球坐标系中极角方向的分量。
磁场 H ( r ) \mathbf{H(r)} H(r) 的方向由 ϕ ^ \hat{\phi} ϕ^ 决定，表示在球坐标系中方位角方向的分量。
在远场区域，电场和磁场的强度均与 sin ⁡ θ \sin \theta sinθ 成正比，表明电磁辐射在垂直于偶极子轴的平面内最强，而在偶极子轴线上最弱。
U ( r ) U(r) U(r) 的形式表示了辐射波的传播特性，包括幅度随距离的衰减和相位的变化。