1 文章信息
文章题目为"Deep Fuzzy Cognitive Maps for Interpretable Multivariate Time Series Prediction"，该文于2019年发表于"IEEE TRANSACTIONS ON FUZZY SYSTEMS"。文章提出了深度模糊认知图（FCM）用于多变量时间序列预测，同时增加了可解释性。
2 摘要
模糊认知图（FCM）是一种用于系统状态预测和可解释知识表示的强大模型。近年来，许多研究通过引入时间因素、不确定性或模糊规则从而提升模型的可解释性，引入模糊神经网络或小波方法从而改进时间序列预测精度。文章提出深度模糊认知图（DFCM）用于多元时间序列预测，该方法结合FCM在可解释性方面的优势和深度神经网络在预测方面的优势。具体而言，为提高预测性能，深度FCM利用一个全连接神经网络来模拟系统中概念（Concept） 之间的连接(Relationships)，并利用一个循环神经网络模拟影响系统动力学的未知外生因素。此外，为提高模型的可解释性，文章提出了一种基于偏导数的方法来测量深度FCM中概念之间的连接强度，并提出了一种替代函数梯度下降算法进行参数推理。深度FCM为构建现实应用中的可解释预测器提供了重要帮助。
3 准备知识
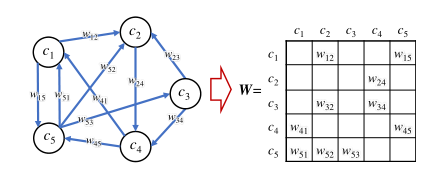
模糊认知图-FCM： 基本的FCM框架由三个元素描述:概念（Concept）、激活状态（Activation States）和关系（Relationships）。其中，概念表示系统中的组件，激活状态表示组件的状态，关系表示组件之间的影响。如上图所示，FCM利用构建一个由I个点构成的加权有向图刻画一个系统。设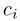
为图的节点，即第i个概念，
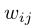表示节点i和节点j之前的加权边，
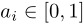表示第i个概念的激活状态，激活状态为1时表示完全激活，激活状态为0时表示完全不激活。对于第i个概念而言，其激活状态为一个动态的时间序列
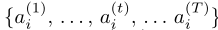，t+1时刻的激活状态可以由下式计算：
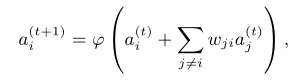
其中，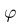
为隶属度函数，将激活状态模糊化至[0,1]区间内。通常情况下，激活状态即为观测的时间序列，但
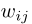通常难以直接获取。给定随机的初值，DHL算法通过t时刻的观测数据调整
：
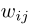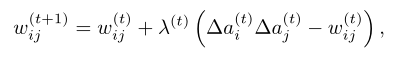
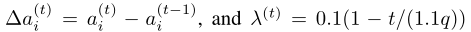
**相关符号定义：**文章涉及的符号定义如下所示。
4 深度模糊认知图-DFCM
模型的框架如图所示，将从4个部分进行介绍：时间序列模糊化、刻画非线性影响、刻画外在因素、衡量概念之间的联系。
时间序列模糊化： 给定一个由若干概念构成的系统，文章设第j个概念对应的原始时间序列为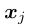
，其值为
。DFCM首先通过z-score对时间序列进行归一化处理：
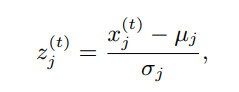
进一步，FCM利用隶属度函数对归一化后的时间序列进行模糊化，得到模糊状态，其中
为Sigmoid函数：
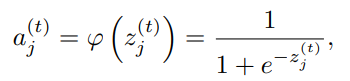
基于上式，给定一个由FDCM预测的模糊状态，为实现预测，文章通过下式对模糊状态进行去模糊化，得到预期的未来值：
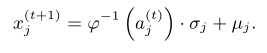
**刻画非线性影响：**基础FCM的一个缺点在于该模型难以刻画非线性关系，为解决这一问题，DFCM通过下式更新激活状态：
其中，
用于刻画系统状态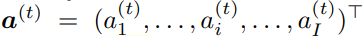
与aj的联系，称为f-函数 ；
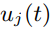用于刻画外在因素（未知因素）对于aj的影响，称为u-函数 。f-函数和u-函数的求和通过Sigmoid函数进行模糊化，从而生成下一个时刻的激活状态。显然，当u-函数为0，f-函数为
时，DFCM退化为基本的FCM。
文章定义f-函数为前馈神经网络，第k层中，第m个神经元在第t时刻的预测值通过下式计算：
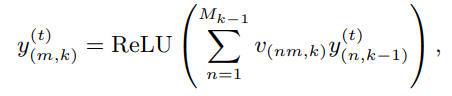
其中，在k=0时，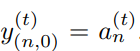
，且在最后一层不使用ReLU函数。
刻画外在因素：DFCM中的外在因素指那些对系统状态a有影响，但不能预先定义和直接测量的因素。以道路运输系统的DFCM为例，在该系统中，路段可以建模为概念，路段是否拥挤可以建模为激活状态。相邻路段的交通速度可以相互影响，形成概念之间的关系，可以用f-函数刻画。然而，交通速度也受到一些外生因素的影响，例如居民的通勤方式、交通管制、重大事件等。由于这些外生因素的状态不能直接测量，因此不能使用预定义的FCM概念来描述它们。为解决这个问题，文章提出基于LSTM的u-函数。具体而言，文章定义u-函数如下：
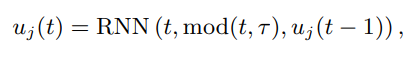
其中，包括三个输入时间步t，以及时间步与预测长度τ的模，以及历史外在因素。文章基于三个考虑将u-函数设计：1. u-函数是与时间步t相关的函数，因为外在因素的影响通常随时间变化；2. 在许多情况下，外在因素具有周期性，如一天、一周、一个月等，因此也采用时间步与预测长度τ的模作为输入；3. 外在因素的动态通常具有"记忆"，即依赖于它们的历史状态。值得注意的是，对于u-函数的计算从t=2时开始。
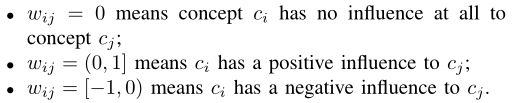
衡量概念之间的联系：FCM的最大优势在于它能够揭示复杂系统中的概念关系。这种优势也被称为FCM的可解释性，如上图所示。简单而言，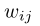
刻画当概念cj增加时，概念ci增加的程度。类似的，文章提出一种基于偏导数的关系计算方式：
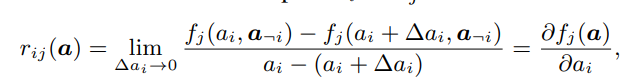
其中，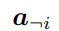
表示除了ai以外的所有激活状态。该偏导数反映了在给定所有激活状态的条件下，当ai增加时，fj增加的幅度。值得注意的是，
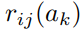是一个关于非关注状态（除ak以外的状态）对应激活状态的函数，为除去这些非关注状态的影响，文章对所有
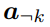的可能值计算了
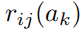的期望值：
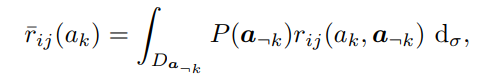
进一步，概念ai对于aj的总影响通过下式计算：
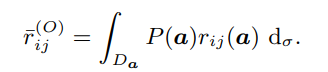
在实际应用中，依据大数定律对上述两式进行近似，由于FCM框架要求关系的值在[−1,1]的范围内，因此文章使用Tanh函数对关系值进行调整。
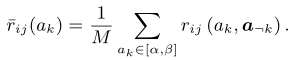
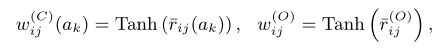
此外，由于文章设定的DFCM模型定义f-函数为全连接神经网络，因此可以通过链式法则对部分偏导数进行计算，如下式所示，其中，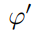
为ReLU函数的导数。
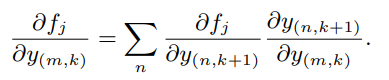
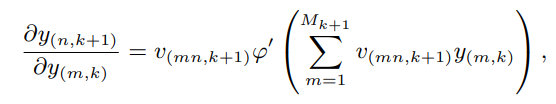
5 目标函数和AFGD算法
目标函数构建： 由于文章构建的DFCM模型刻画了未知的外在因素，因此预测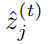值
和真实值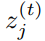
之间的误差应该是一个随机误差，文章假设
服从0均值的高斯噪声，文章利用最大似然估计（MLE）构建目标函数：
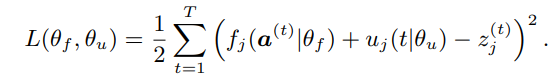
AFGD算法： DFCM与基本FCM的最大区别在于DFCM包含了许多深度神经网络成分，如f-函数和u-函数。然而，传统的FCM训练算法不能直接用于训练深度神经网络，因此文章基于反向传播算法提出一种新的训练方法，称为交替函数梯度下降(AFGD)。AFGD算法通过迭代的方式学习f-函数和u-函数中的参数，如下式所示：
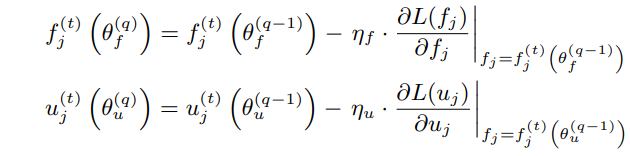
进一步，上述计算公式可转化为下述公式：
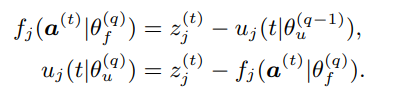
上述两式可以直观地理解为u-函数和f-函数交替使用对方的预测残差来训练它们的参数。F-函数的预测残差是无法用内部FCM概念建模的影响，即外在因素的影响，因此应由u-函数吸收。相反，u-函数的预测残差应该通过f-函数进行刻画。算法总结如下：
6 实验
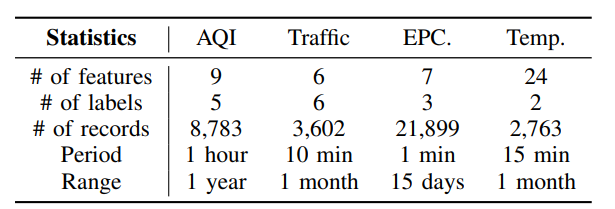
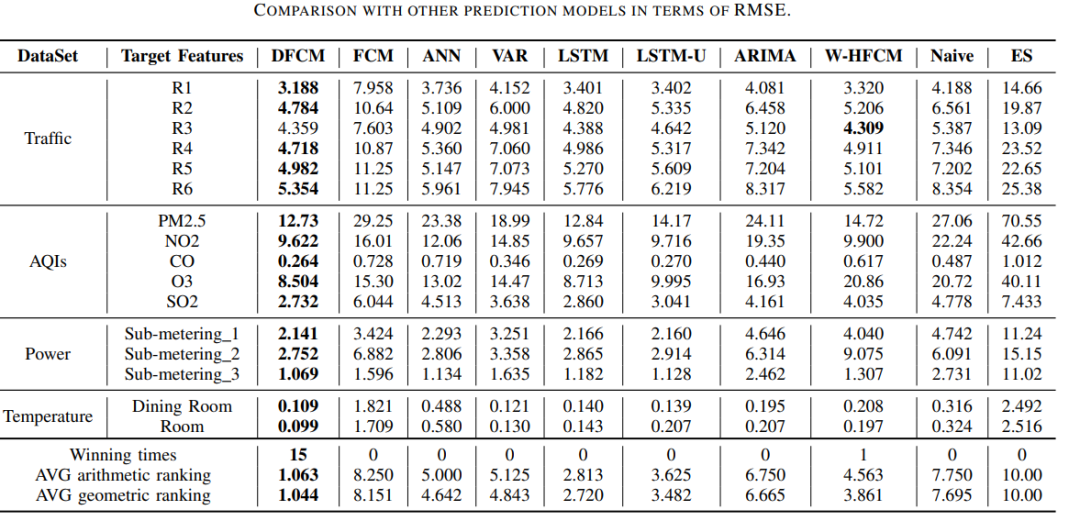
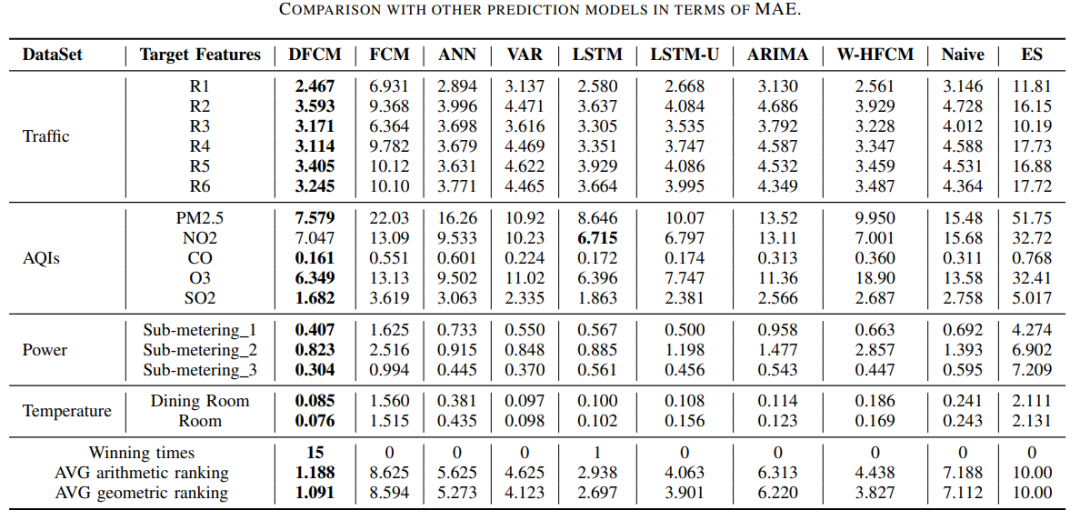
文章选用的数据集如上表所示，包括空气质量数据集、交通速度数据集、电力消耗数据集和温度数据集。具体而言，空气质量指数（AQI）： 该数据集包含2017年2月至2018年2月在中国北京收集的气象和空气质量指数的时间序列。文章使用4个气象指标和5个时间点的空气质量指标作为输入来预测时间点t+1的空气质量指数；交通数据集（Traffic）： 该数据集包含2016年4月1日至30日北京6个路段的交通速度。文章使用t时刻所有路段的交通速度作为输入来预测t+1时刻每个路段的速度。电力消耗数据集（EPC）： 该数据集包含一个家庭的电力消耗测量数据3。不同的电量和一些分计量值是可用的。文章实验所用数据集对应的时间跨度为2016年12月16日至31日。文章使用四个电量和三个分计量值作为输入来预测下一个周期的三个分计量值。**温度数据集（Temp）：**该数据集包含24个特征，这些特征是从安装在家庭房屋中的监控系统收集的。文章使用的数据集对应时间跨度为2012年3月3日至4月11日。文章使用时间t的所有特征来预测时间t+1时餐厅和房间的室内温度。实验结果如下表所示，可以看到DFCM取得了较好的预测性能。
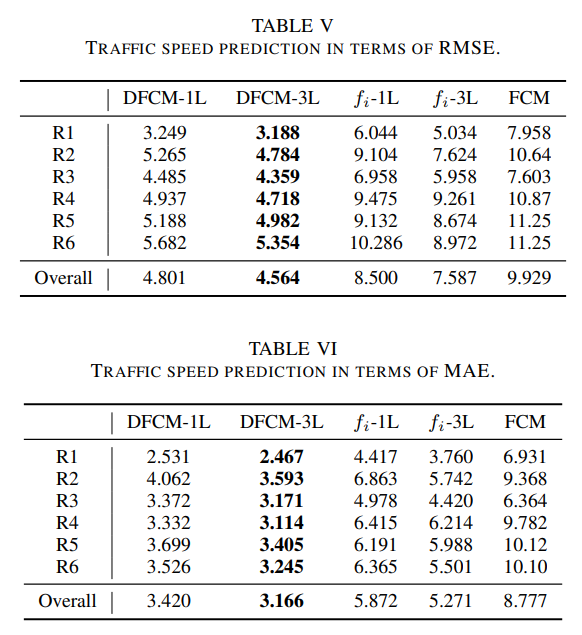
此外，文章利用交通速度数据集对模型的组成成分进行消融实验，DFCM-1L：该模型包含一个f-函数隐藏层和一个u-函数隐藏层；DFCM-3L: 该模型包含三个f-函数隐藏层和一个u-函数隐藏层；fi-1L：该模型仅包含一层f-函数隐藏层；fi-3L: 该模型仅包含三个f-函数隐藏层；FCM：基础的FCM模型。实验结果如下。
7 总结
文章提出了一种基于深度神经网络的模糊认知图模型，称为DFCM，以实现可解释的多元时间序列预测。DFCM模型将深度神经网络模型引入到FCM的知识表示框架中，从而将FCM在解释方面的优势和深度神经网络在预测方面的优势集成到同一个模型中。文章通过真实数据集验证了深度FCM在可解释性和预测能力方面的优异性能。深度FCM为构建现实应用中的可解释预测器提供了重要帮助。