文章目录
前言
前面发布的【图形学初识】系列文章,坐标基本上都指代屏幕空间的二维坐标,迟迟没有进入真正的3维世界。为了真正进入三维世界,就需要存在一种工具将三维坐标映射为二维坐标,这个工具就涉及到数学中的线性代数中的一些概念,如:矩阵、向量、行列式等等!本章节就针对这些概念和相关计算做说明!
正文
向量
什么是向量?
概念:向量的相对概念是标量,以下是两者的对比:
向量: 既有大小,又有方向;
标量: 只有大小,没有方向;
举个例子:
向量: 速度、加速度、力等
标量: 颜色、温度、质量等
基本表示: a ⃗ = A B ⃗ = B − A \vec{a} = \vec{AB} = B - A a =AB =B−A 。一个不太准确,但又十分形象的图形表示如下图:

a ⃗ \vec{a} a 的大小:AB之间的距离
a ⃗ \vec{a} a 的方向:A指向B的这个方向
三维空间下,假设 A = ( x 0 , y 0 , z 0 ) , B = ( x 1 , y 1 , z 1 ) A = (x_0, y_0, z_0),B = (x_1, y_1, z_1) A=(x0,y0,z0),B=(x1,y1,z1),则 A B ⃗ = B − A = ( x 1 − x 0 , y 1 − y 0 , z 1 − z 0 ) \vec{AB} = B - A = (x_1 - x_0, y_1 - y_0, z_1 - z_0) AB =B−A=(x1−x0,y1−y0,z1−z0)
本质上,上述的坐标表示法,其实是针对三维空间正交向量基的i、j、k的加权组合,但是因为目前还没有讲向量乘法、向量加法,所以没法解释,可以直观的认为就是这样做!
向量涉及哪些常见计算?
1、取模
假设 A = ( x 0 , y 0 , z 0 ) , B = ( x 1 , y 1 , z 1 ) , A B ⃗ = ( x 1 − x 0 , y 1 − y 0 , z 1 − z 0 ) A = (x_0,y_0,z_0),B=(x_1,y_1,z_1), \vec{AB} = (x_1-x_0,y_1-y_0,z_1-z_0) A=(x0,y0,z0),B=(x1,y1,z1),AB =(x1−x0,y1−y0,z1−z0),记 ∥ A B ⃗ ∥ \|\vec{AB}\| ∥AB ∥ 是 A B ⃗ \vec{AB} AB 模,本质就是向量的长度
计算公式如下:
∥ A B ⃗ ∥ = ( x 1 − x 0 ) 2 + ( y 1 − y 0 ) 2 + ( z 1 − z 0 ) 2 \|\vec{AB}\| = \sqrt{(x_1-x_0)^2 + (y_1-y_0)^2 + (z_1-z_0)^2} ∥AB ∥=(x1−x0)2+(y1−y0)2+(z1−z0)2
2、归一化
假设 A = ( x 0 , y 0 , z 0 ) , B = ( x 1 , y 1 , z 1 ) , A B ⃗ = ( x 1 − x 0 , y 1 − y 0 , z 1 − z 0 ) A = (x_0,y_0,z_0),B=(x_1,y_1,z_1), \vec{AB} = (x_1-x_0,y_1-y_0,z_1-z_0) A=(x0,y0,z0),B=(x1,y1,z1),AB =(x1−x0,y1−y0,z1−z0),记 A B ^ \hat{AB} AB^ 是 A B ⃗ \vec{AB} AB 的归一化向量
归一化本质:计算一个方向不变,长度变为1的对应向量
计算公式如下:
A B ^ = A B ⃗ ∥ A B ⃗ ∥ \hat{AB} = \frac{\vec{AB}}{\|\vec{AB}\|} AB^=∥AB ∥AB
3、向量加法
假设 a ⃗ = ( x 0 , y 0 , z 0 ) , b ⃗ = ( x 1 , y 1 , z 1 ) \vec{a} = (x_0,y_0,z_0),\vec{b} =(x_1,y_1,z_1) a =(x0,y0,z0),b =(x1,y1,z1) 那么 c ⃗ = a + b ⃗ = ( x 1 + x 0 , y 1 + y 0 , z 1 + z 0 ) \vec{c} = \vec{a + b} = (x_1+x_0,y_1+y_0,z_1+z_0) c =a+b =(x1+x0,y1+y0,z1+z0)
代数解释:对应坐标相加
几何解释:
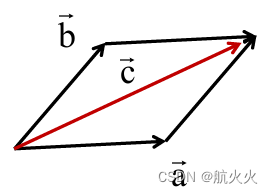
(1)两向量移动到统一起点,构成平行四边形,副对角线即为加和结果
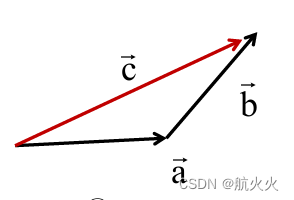
(2)把b向量移动到a向量的末尾,从a起点连接b终点,得到的向量即为加和结果
4、向量减法
假设 a ⃗ = ( x 0 , y 0 , z 0 ) , b ⃗ = ( x 1 , y 1 , z 1 ) \vec{a} = (x_0,y_0,z_0),\vec{b} =(x_1,y_1,z_1) a =(x0,y0,z0),b =(x1,y1,z1) 那么 c ⃗ = b − a ⃗ = ( x 1 − x 0 , y 1 − y 0 , z 1 − z 0 ) \vec{c} = \vec{b - a} = (x_1-x_0,y_1-y_0,z_1-z_0) c =b−a =(x1−x0,y1−y0,z1−z0)
代数解释:对应坐标相减
几何解释:向量a的末端连接向量b末端的一个新向量
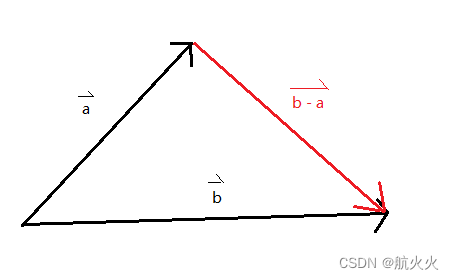
5、向量与标量乘
假设 a ⃗ = ( x 0 , y 0 , z 0 ) \vec{a} = (x_0,y_0,z_0) a =(x0,y0,z0) 那么 c ⃗ = k a ⃗ = ( k x 0 , k y 0 , k z 0 ) \vec{c} = k\vec{a} = (kx_0,ky_0,kz_0) c =ka =(kx0,ky0,kz0)
代数解释:对应坐标乘标量k
几何解释:当 k ! = 0 k\ !=0 k !=0,向量等比例调整长度,k为缩放比例
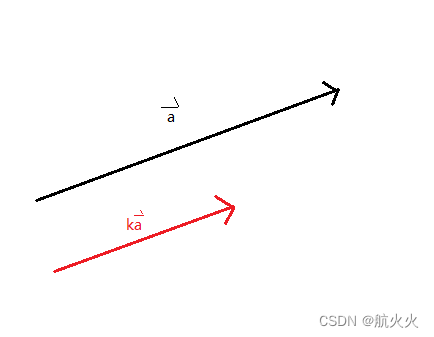
6、向量点乘(内积)
假设 a ⃗ = ( x 0 , y 0 , z 0 ) , b ⃗ = ( x 1 , y 1 , z 1 ) \vec{a} = (x_0,y_0,z_0),\vec{b} =(x_1,y_1,z_1) a =(x0,y0,z0),b =(x1,y1,z1) 那么记点乘 c ⃗ = a ⃗ ⋅ b ⃗ = x 1 x 0 + y 1 y 0 + z 1 z 0 \vec{c} = \vec{a} \cdot \vec{b} = x_1x_0 + y_1y_0+z_1z_0 c =a ⋅b =x1x0+y1y0+z1z0
注意:点乘的结果是一个标量
代数解释:对应坐标相乘然后相加
几何解释: a ^ ⋅ b ^ = ∥ a ⃗ ∥ ∥ b ⃗ ∥ cos θ \hat a \cdot \hat b = \|\vec{a}\|\|\vec{b}\|\cos \theta a^⋅b^=∥a ∥∥b ∥cosθ, 如下图所示
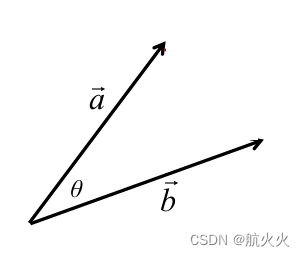
7、向量投影
假设 a ⃗ = ( x 0 , y 0 , z 0 ) , b ⃗ = ( x 1 , y 1 , z 1 ) \vec{a} = (x_0,y_0,z_0),\vec{b} =(x_1,y_1,z_1) a =(x0,y0,z0),b =(x1,y1,z1) 那么记 a ⃗ \vec a a 在 b ⃗ \vec b b 上的投影为 a p r j b ⃗ \vec{a_{prjb}} aprjb ,计算公式如下:
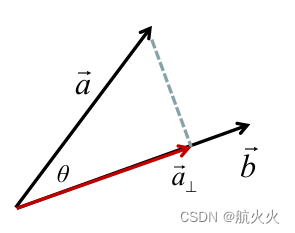
a p r j b ⃗ = b ^ ∗ ∥ a ⊥ ⃗ ∥ = b ⃗ ∥ b ⃗ ∥ ∗ cos θ ∗ ∥ a ⃗ ∥ = b ⃗ ∥ b ⃗ ∥ ∗ a ⃗ ⋅ b ⃗ ∥ a ⃗ ∥ ∥ b ⃗ ∥ ∗ ∥ a ⃗ ∥ = a ⃗ ⋅ b ⃗ ∥ b ⃗ ∥ 2 b ⃗ \begin{align} \vec{a_{prjb}} &= \hat b * \|\vec{a_{\perp}}\|\\ &=\frac{\vec b}{\|\vec b\|} * \cos \theta * \|\vec a\|\\ &=\frac{\vec b}{\|\vec b\|} * \frac{\vec a \cdot \vec b}{\|\vec a\| \|\vec b\|} * \|\vec a\|\\ &=\frac{\vec a \cdot \vec b}{\|\vec b\|^2}\vec b \end{align} aprjb =b^∗∥a⊥ ∥=∥b ∥b ∗cosθ∗∥a ∥=∥b ∥b ∗∥a ∥∥b ∥a ⋅b ∗∥a ∥=∥b ∥2a ⋅b b
假设被投影的向量为单位向量,则结果可以简化: a p r j b ⃗ = ( a ⃗ ⋅ b ⃗ ) b ⃗ \vec{a_{prjb}} = (\vec a \cdot \vec b)\ \vec b aprjb =(a ⋅b ) b
向量有哪些基本应用?
(1)判断两向量是否同向(重要)

利用向量点乘的结果判断,如果结果为负数,则不是同向,如果结果为正数,则同向。
(2)计算投影
略(上述已给出计算公式)
(3)计算夹角
略(也是利用点乘,计算 cos θ \cos \theta cosθ,从而计算出夹角)
矩阵
什么是矩阵?
矩阵本质就是一个二维数组,有行、有列,其中存储许多数字,每个数字叫做矩阵的元素。第i行、j列的记作 a i j a_{ij} aij,当行和列相等时,我们叫做方阵!
如下图就是3x3的方阵,,我们常记作矩阵为 M M M :
10 12 30 − 1 3 0 2 96 123 \] \\begin{bmatrix} 10 \& 12 \& 30 \\\\ -1 \& 3 \& 0 \\\\ 2 \& 96 \& 123\\\\ \\end{bmatrix} 10−1212396300123 当方阵的只有主对角线元素为1,其余所有元素为0,我们记矩阵为单位矩阵,记 I n I_n In,如下图: \[ 1 0 0 0 1 0 0 0 1 \] \\begin{bmatrix} 1 \& 0 \& 0 \\\\ 0 \& 1 \& 0 \\\\ 0 \& 0 \& 1 \\\\ \\end{bmatrix} 100010001 #### 矩阵涉及哪些常见计算? ##### 1、矩阵加法 前提:两矩阵行列数相同 计算规则:对应元素相加 ##### 2、矩阵减法 前提:两矩阵行列数相同 计算规则:对应元素相减 ##### 3、矩阵乘法 前提:矩阵 A A A 左乘矩阵 B B B ,要求A的列数与B的行数相同 计算规则:假设矩阵 C C C 的每个元素为 c i j c_{ij} cij ,矩阵 A A A的每个元素为 a i j a_{ij} aij ,矩阵 B B B的每个元素为 b i j b_{ij} bij ,如果 C = A B C = AB C=AB 则 C C C的每个元素: c i j = ( a i 0 a i 1 a i 2 . . . a i n ) ⋅ ( b 0 j b 1 j b 2 j . . . b n j ) c_{ij} = \\begin{pmatrix} a_{i0}\\\\ a_{i1}\\\\ a_{i2}\\\\ ...\\\\ a_{in}\\\\ \\end{pmatrix} \\cdot \\begin{pmatrix} b_{0j}\\\\ b_{1j}\\\\ b_{2j}\\\\ ...\\\\ b_{nj}\\\\ \\end{pmatrix} cij= ai0ai1ai2...ain ⋅ b0jb1jb2j...bnj 给个示例图: 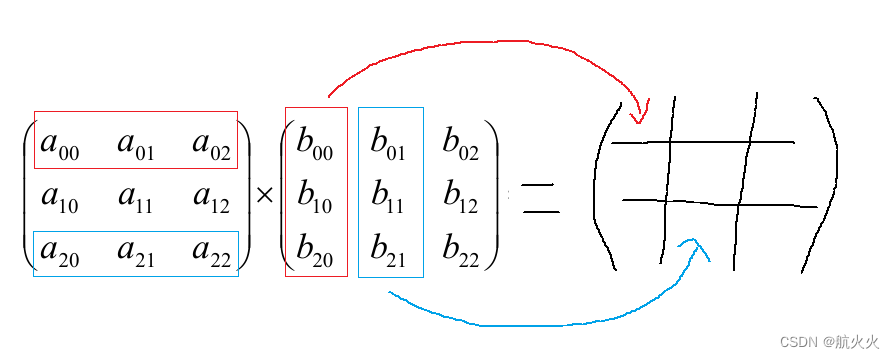 **几个常见的乘法性质:** ( A B ) C = A ( B C ) A ( B + C ) = A B + A C ( A + B ) C = A C + B C (AB)C = A(BC)\\\\ A(B+C) = AB + AC\\\\ (A+B)C = AC + BC (AB)C=A(BC)A(B+C)=AB+AC(A+B)C=AC+BC **注意:** 矩阵乘法没有交换律,一般来说: A B ! = B A AB\\ != BA AB !=BA ##### 4、矩阵和向量乘法 我们可以将向量理解为列或者行为1的矩阵,这样问题就转化为矩阵的乘法类似,不多赘述! 如下图: 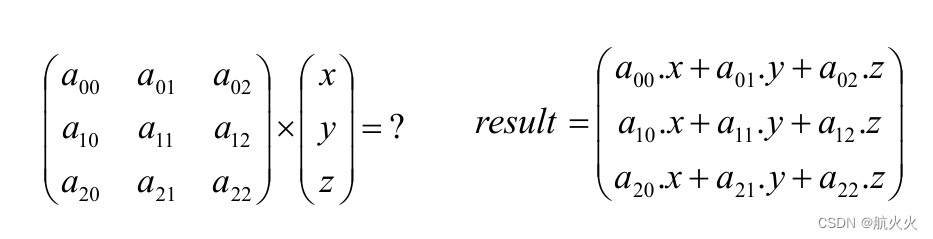 #### 矩阵有哪些基本应用? 无所不能,在图形学领域最重要的概念就是MVP变换,本质上就是对应三个矩阵!这方面内容会在后面章节详细讲解哦!大家拭目以待! ## 结尾:喜欢的小伙伴可以点点关注+赞哦 希望对各位小伙伴能够有所帮助哦,永远在学习的道路上伴你而行, 我是航火火,火一般的男人!