目录
- [1. 作者介绍](#1. 作者介绍)
- [2. 什么是AdaBoost?](#2. 什么是AdaBoost?)
- [2.1 什么是弱分类器](#2.1 什么是弱分类器)
-
- [2.2 什么是强分类器](#2.2 什么是强分类器)
- [2.3 如何自适应增强](#2.3 如何自适应增强)
- [2.4 如何组合弱分类器成为一个强分类器?](#2.4 如何组合弱分类器成为一个强分类器?)
- [3. 什么是Wine数据集](#3. 什么是Wine数据集)
-
- [3.1 Wine 数据集](#3.1 Wine 数据集)
- [3.2 Wine 数据集结构](#3.2 Wine 数据集结构)
- [4. 使用AdaBoost分类方法实现对Wine数据集分类](#4. 使用AdaBoost分类方法实现对Wine数据集分类)
- [5. 完整代码](#5. 完整代码)
1. 作者介绍
赵俊旗,男,西安工程大学电子信息学院,2023级研究生
研究方向:水下目标检测与信号处理
电子邮件:2230648022@qq.com
徐达,男,西安工程大学电子信息学院,2023级研究生,张宏伟人工智能课题组
研究方向:机器视觉与人工智能
电子邮件:1374455905@qq.com
2. 什么是AdaBoost?
AdaBoost (Adaptive Boosting-自适应增强), AdaBoost通过组合多个弱分类器(那些比随机猜测略好的分类器)来构建一个强分类器。
这短短一句话读完就会发现信息量挺大的,什么是弱分类器?什么是强分类器?是如何进行自适应增强的?以及怎么组合成一个强分类器的?把这四个问题搞懂,可能就会更容易理解AdaBoost.
2.1 什么是弱分类器
弱分类器是指分类准确率在 60% 到 80% 之间的分类器,即比随机预测略好,但准确率不高。比如一个二分类问题,随机猜测进行分类的正确率都有50%,所以弱分类器比随即猜测略好一些。
弱分类器的常用类型包括:决策树桩、K近邻分类器、朴素贝叶斯分类器等。
如决策树桩:

2.2 什么是强分类器
强分类器是指分类准确率在 90% 以上的分类器。
2.3 如何自适应增强
这是理解Adaboost的一个重点!其核心思想是关注那些被前一轮弱分类器错误分类的样本,通过逐步调整样本的权重,使后续的弱分类器更注重这些困难样本,从而提高整体分类器的准确性。
抽象的概念不容易理解? 举个例子:
有一个简单的分类任务,将5个颜色分别为红色(标签+1)和蓝色(标签-1)的圆点分开,使用3个决策树桩作为弱分类器。
STEP1:使用第一个弱分类器h1(即使用第1个决策树)
(1)初始化样本权重(使所有样本权重相等),因为共5个圆点,所以共5个样本,每个样本的权重为wi =1/5。
(2)计算第一个弱分类器的错误率ϵ1和权重α1
①计算第一个弱分类器错误率ϵ1:
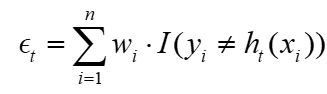
其中wi为样本权重(即上述的1/5), I(yi≠hi(xi))为指示函数, hi(xi)为弱分类器的预测, yi为真实值,指示函数在这里的意义是当预测与真实值相等时,指示函数为0;当预测与真实值不相等时,指示函数为1,所以在这里就相当于增加了错误样本的权重,对应上述"更注重分类错误的样本"。
如我们这5个样本里有两个被分类错误,分别是第1个和第3个,则错误率ϵ1计算为:
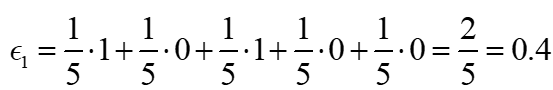
②计算第一个弱分类器的权重α1
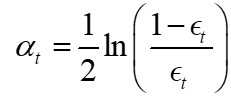
其中ϵt为第①步计算出来的错误率。可以根据表达式看到,错误率越大,此弱分类器的权重越小,此弱分类器在所有的3个弱分类器的话语权也就越低。反之,错误率越小,其权重越大,此弱分类器在所有的3个弱分类器的话语权也就越高。
所以第一个弱分类器的权重α1计算为:
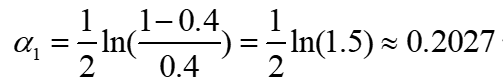
(3)更新样本权重
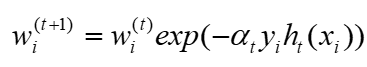
根据初始样本权重wi和计算出来的第一个弱分类器的权重α1以及其是否被真实预测可得到新的样本权重。其中若被真实预测, yiht(xi)的值为11或(-1) (-1)均为1,若没有被真实预测,则yiht(xi)的值为1*(-1)或(-1)*1均为-1,可以根据表达式观察到,当其没有被真实预测时,其下一次的权重将会增大。
所以经过第一个弱分类器得到新的样本权重为:
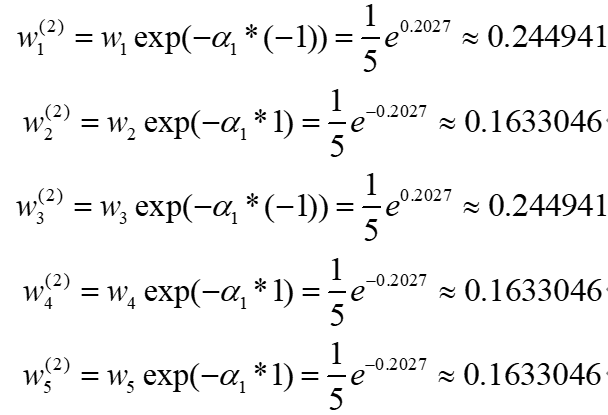
可以看到,在第1个和第3个样本被错误分类时,其样本的权重会增大,回扣AdaBoost核心思想里"更注重分类错误的样本"。
现在经过第一个分类器后,可以得到其样本新的权重 和第1个弱分类器的权重α1。
STEP2: 使用第二个弱分类器h2(即使用第2个决策树),此时不再使所有样本权重相等,而是使用经第一个弱分类器更新完成的新的权重wi(2),计算第2个弱分类器的错误率ϵ2从而得到权重α2,进而可以得到一个更新的样本权重wi(3)(即重复STEP1)。
STEP3:使用第三个弱分类器h3(即使用第3个决策树),此时使用经第二个弱分类器更新完成的更新的权重wi(3),计算第3个弱分类器的错误率ϵ3从而得到权重α3,进而可以得到一个最新的样本权重wi(4)(即重复STEP1)。
好了,现在得到了三个弱分类器的权重,是时候要将他们组合在一起了。
2.4 如何组合弱分类器成为一个强分类器?
强分类器𝐻(𝑥)的预测结果通过弱分类器加权投票决定。
现在有三个弱分类器 h1,h2,h3 及其对应的权重 α1,α2,α3,每个弱分类器会对输入样本进行分类,得到的结果是要么是+1要么是-1(即二分类任务中的类别标签)。
现在有一个输入样本x,
1.弱分类器1(h1)对输入样本x的预测是 -1,权重α1 = 0.2027
2.弱分类器2(h2)对输入样本x的预测是 +1,权重α2= 0.5
3.弱分类器3(h3)对输入样本x的预测是 +1,权重α3 =0.8
组合最终的强分类器
强分类器 𝐻(𝑥)的预测结果通过加权投票决定:
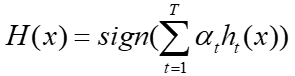
其中sign(x)为符号函数,当x大于0时值为+1,x小于0时值为-1。所以加权投票组成强分类器分类结果为:
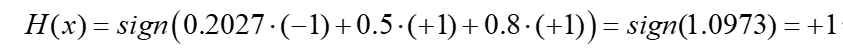
至此我们更能清晰地理解何为AdaBoost自适应增强。
注意:一般的AdaBoost自适应增强需要多个弱分类器才能达到最好的效果,此处为了简便理解,选择3个弱分类器;同时要注意理解样本的权重和弱分类器的权重,样本权重是为了下一个弱分类器更关注上一个分类错误的样本,弱分类器的权重是为了看出其在构建强分类器时话语权的强弱。
AdaBoost的部分优点如下:
简单且灵活:AdaBoost可以与任何弱分类器一起使用,且易于实现。
无需调整参数:AdaBoost对弱分类器的选择和参数设定相对不敏感。
自动聚焦难分类样本:通过动态调整样本权重,AdaBoost使后续的分类器更关注难分类的样本。
AdaBoost的部分缺点如下:
对噪声敏感:因为错误分类的样本权重会增加,数据集中存在的噪声点可能会导致模型过拟合。
需要多个弱分类器:AdaBoost的性能依赖于多个弱分类器的结合,单个弱分类器的性能不能太差。
3. 什么是Wine数据集
Wine 数据集是一个经典的机器学习数据集,用于多分类任务。该数据集包含来自意大利同一地区的三种不同类型的葡萄酒的化学分析结果。每种葡萄酒的特征和类别标签都已标注,用于分类模型的训练和评估。
3.1 Wine 数据集

3.2 Wine 数据集结构
在python的scikit-learn 库中,Wine 数据集可以直接通过 load_wine 函数加载,其中alcohol, malic_acid, ash,等是特征列,target 是目标变量,表示红酒的类别。
导入并查看前5行数据(以图片展示,完整程序附后):
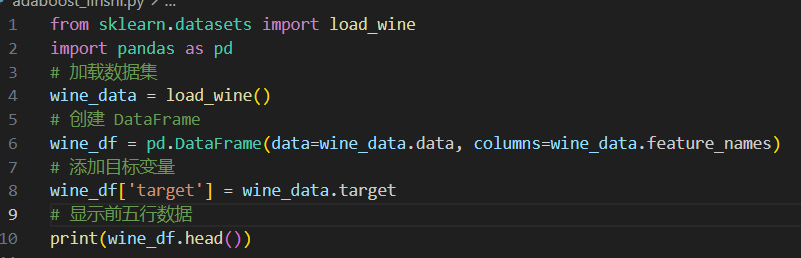
其数据集结构为:

4. 使用AdaBoost分类方法实现对Wine数据集分类
(1)首先pip安装scikit-learn 和 pandas 库
python
pip install scikit-learn pandas(2) 加载并预处理数据集
• 使用 scikit-learn 自带的 Wine 数据集,它已经分为特征数据x和目标标签y
• 对特征数据进行标准化处理,确保每个特征的均值为0,方差为 1,有助于提升模型的性能。
• 将数据集划分为训练集(70%)和测试集(30%)
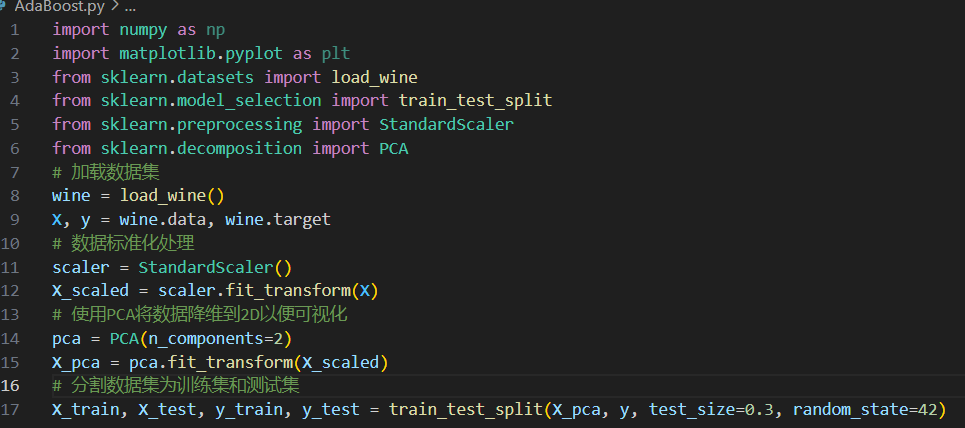
(3)构建并训练 AdaBoost 模型
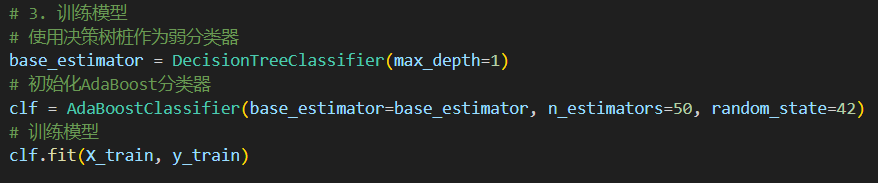
• 使用决策树桩作为弱分类器
• 构建一个 AdaBoost 分类器,并用训练集数据训练模型n_estimators=50 表示使用 50 个弱分类器
(4)预测与评估
对测试集进行预测,并使用准确率来评估模型的性能。
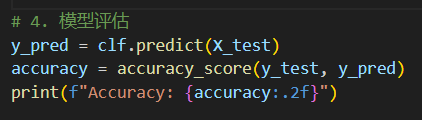
打印输出:

(5)可视化分类结果
①混淆矩阵
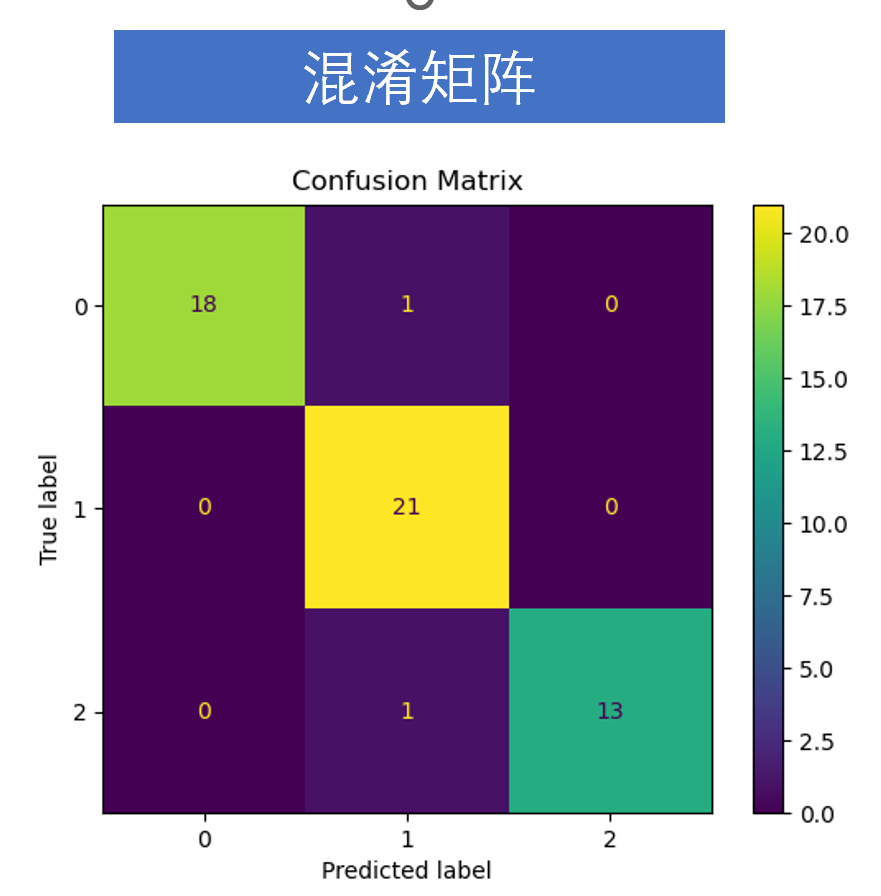
③决策边界
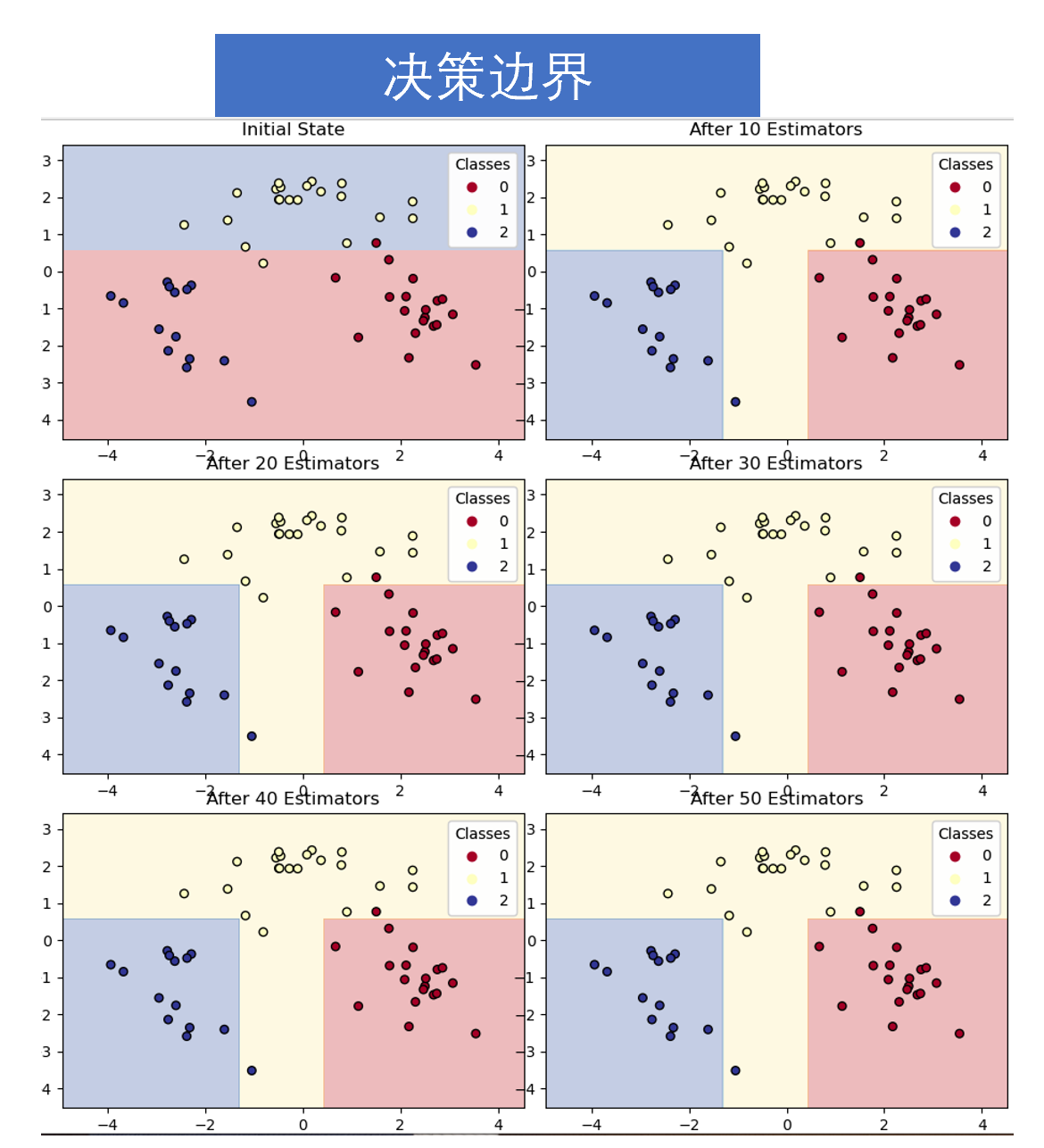
④学习曲线
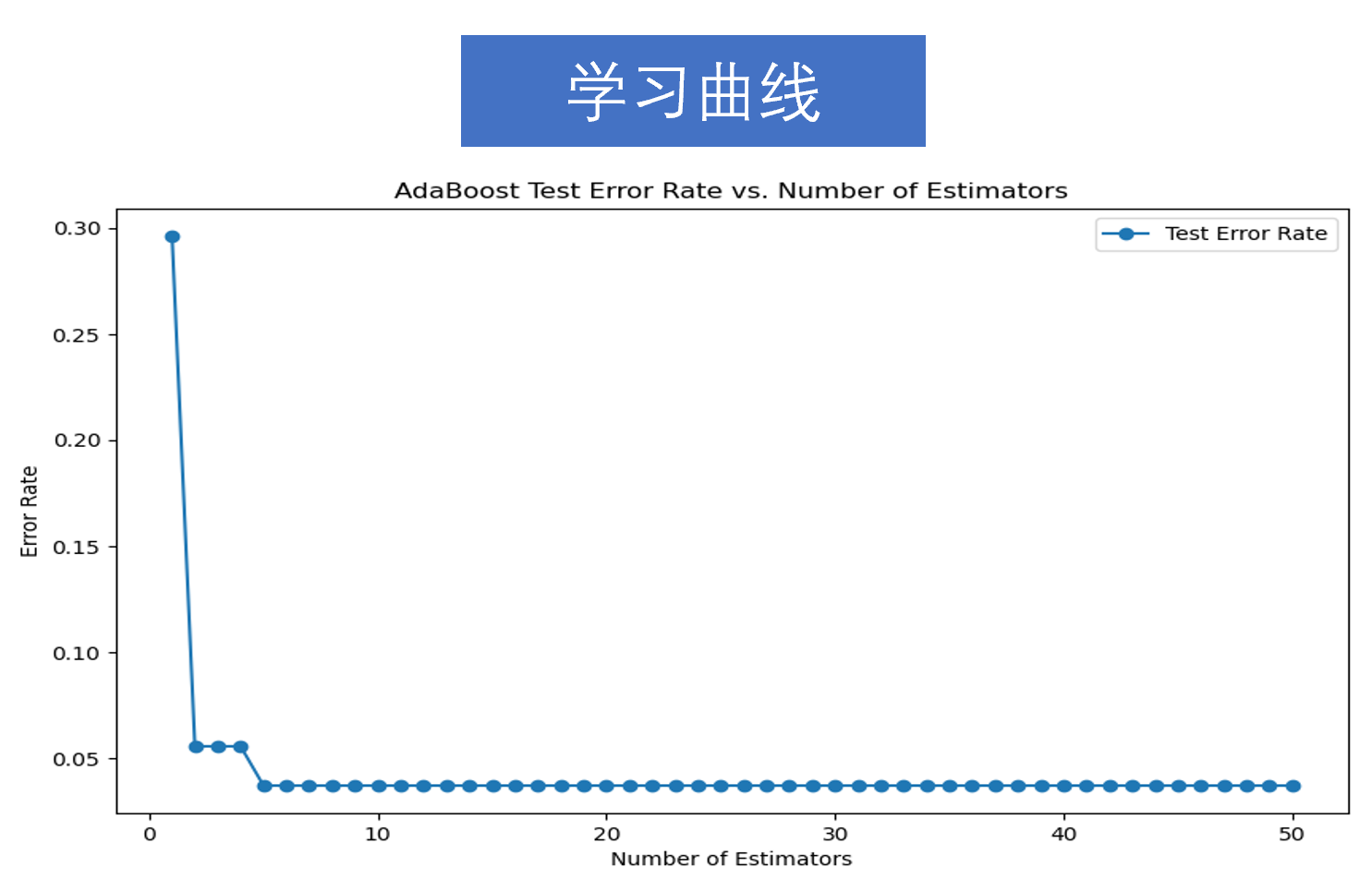
⑤特征重要性
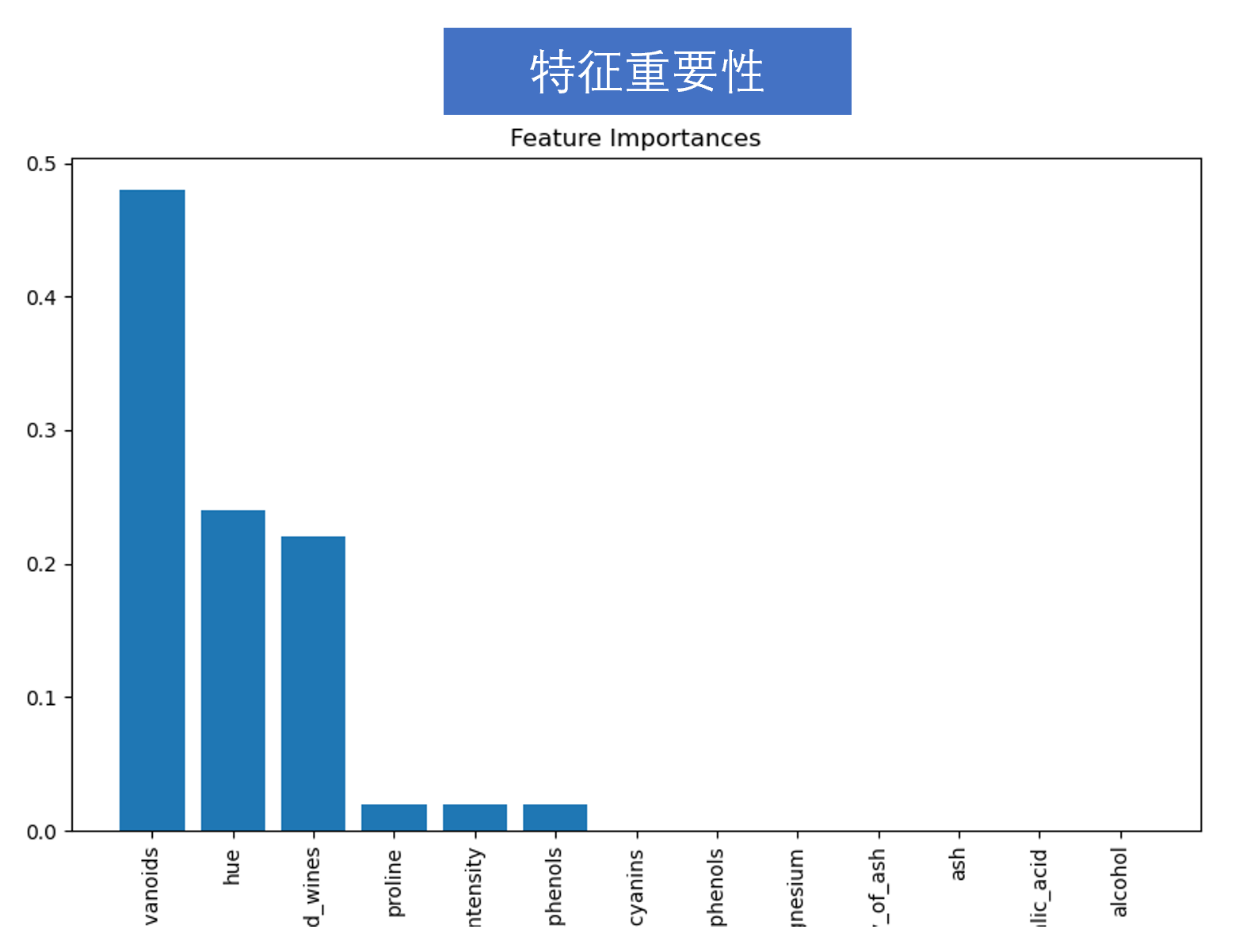
另外:可以考虑改变训练集和测试集比例对结果的影响,以及改变迭代次数(弱分类器个数)对结果的影响。
5. 完整代码
python
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from sklearn.datasets import load_wine
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
from sklearn.ensemble import AdaBoostClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.metrics import accuracy_score, confusion_matrix, ConfusionMatrixDisplay
# 加载数据集
wine = load_wine()
X, y = wine.data, wine.target
# 数据标准化处理
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
# 使用PCA将数据降维到2D以便可视化
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X_scaled)
# 分割数据集为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X_pca, y, test_size=0.3, random_state=42)
# 使用决策树桩作为弱分类器
base_estimator = DecisionTreeClassifier(max_depth=1)
# 初始化AdaBoost分类器,训练模型n_estimators=50,即为50个弱分类器(可更改分类器个数观察分类效果)
clf = AdaBoostClassifier(base_estimator=base_estimator, n_estimators=50, random_state=42)
clf.fit(X_train, y_train)
# 评估模型,观察准确率
y_pred = clf.predict(X_test)
accuracy = accuracy_score(y_test, y_pred)
print(f"Accuracy: {accuracy:.2f}")
# 绘制混淆矩阵
cm = confusion_matrix(y_test, y_pred, labels=clf.classes_)
disp = ConfusionMatrixDisplay(confusion_matrix=cm, display_labels=clf.classes_)
disp.plot()
plt.title("Confusion Matrix")
plt.show()
# 绘制决策边界函数
def plot_decision_boundary(X, y, clf, ax, title=""):
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.02),
np.arange(y_min, y_max, 0.02))
Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
ax.contourf(xx, yy, Z, alpha=0.3, cmap=plt.cm.RdYlBu)
scatter = ax.scatter(X[:, 0], X[:, 1], c=y, s=30, edgecolor='k', cmap=plt.cm.RdYlBu)
legend = ax.legend(*scatter.legend_elements(), title="Classes")
ax.add_artist(legend)
ax.set_title(title)
# 初始化决策树桩分类器并训练初始模型
initial_clf = DecisionTreeClassifier(max_depth=1)
initial_clf.fit(X_train, y_train)
# 绘制初始状态和每10次迭代的决策边界观察第1、10、20、30、40、50次迭代的决策边界
fig, axes = plt.subplots(3, 2, figsize=(20, 15))
axes = axes.flatten()
plot_decision_boundary(X_test, y_test, initial_clf, axes[0], title="Initial State")
for i in range(1, 6):
n_estimators = i * 10
clf_partial = AdaBoostClassifier(base_estimator=base_estimator, n_estimators=n_estimators, random_state=42)
clf_partial.fit(X_train, y_train)
plot_decision_boundary(X_test, y_test, clf_partial, axes[i], title=f"After {n_estimators} Estimators")
plt.tight_layout()
plt.show()
# 提取和显示特征重要性
original_clf = AdaBoostClassifier(base_estimator=base_estimator, n_estimators=50, random_state=42)
original_clf.fit(X_scaled, y)
feature_importances = np.mean([
tree.feature_importances_ for tree in original_clf.estimators_
], axis=0)
# 特征重要性可视化,观察数据集哪几个特征为主要影响因素
features = wine.feature_names
indices = np.argsort(feature_importances)[::-1]
plt.figure(figsize=(10, 6))
plt.title("Feature Importances")
plt.bar(range(X.shape[1]), feature_importances[indices], align="center")
plt.xticks(range(X.shape[1]), np.array(features)[indices], rotation=90)
plt.xlim([-1, X.shape[1]])
plt.show()
# 绘制学习曲线,观察其错误率随迭代次数的变化
n_estimators = len(clf.estimators_)
error_rate = np.zeros(n_estimators)
for i, y_pred_iter in enumerate(clf.staged_predict(X_test)):
error_rate[i] = 1 - accuracy_score(y_test, y_pred_iter)
plt.figure(figsize=(10, 6))
plt.plot(range(1, n_estimators + 1), error_rate, marker='o', label='Test Error Rate')
plt.xlabel('Number of Estimators')
plt.ylabel('Error Rate')
plt.title('AdaBoost Test Error Rate vs. Number of Estimators')
plt.legend(loc='best')
plt.show()