小波分析方法近些年逐步得到发展的一门数学分析技术,它对许多学科都有十分重要的影响。与傅立叶变换等其他传统方法相比,小波分解的方法中所用的小波基有着多种多样的结构,总结来说又包括正交小波系与非正交小波系。正交小波在信号处理领域目前有着最多的应用,如Haar小波、Daubechies小波系等。非正交小波这些年来也逐步得到发展和应用,最具有代表性之一的就是Morlet小波。
1988年S.Mallat首先提多分辨率分析这一观点,结合小波基的结构特点,从从几何角度分析了正交小波,并提出了一种基于正交小波的快速算法,即Mallat算法。正因为有了Mallat快速算法,使正交小波在多个领域有了广泛的应用。与有着Mallat算法的正交小波不同,关于非正交小波理论研究及使用的文章相对较少,实际使用也不多见,但最近一些年发展很快。主要有如下几点:
(1)广泛地应用于各类机械故障诊断中。当信噪比不高,而又要被测量的信号有许多需要关注的频带且随时间变化时,非正交小波是一种十分有效的处理方法。
(2)在某些结构封闭,或者正在高速运转的机械进行信号特征提取时,非正交小波有着非常好的效果。
(3)非正交小波在非破坏性监测方面成果显著,如从高速运转的飞机发动机位置采集振动信号,进而提取细节信息来判断发动机的运行情况。
(4)非正交小波在也应用于结构模态参数识别中。
(5)基于非正交小波的滤波技术研究。其中重要研究成果有:基于母小波的低通滤波算法;扫频和脉冲两种激励下的Morlet小波去噪算法。
(6)通过Morlet小波变换获得信号强度随时间变换规律。如家用电器里常用的开关零件,在切换的瞬间会产生高强度的信号变化,通过分析此时的信号可以得到其内部零件的状态、在熔炉运行过程中通过分析其瞬时电压信号改变来判断其运转状态、用Morlet小波变换的方法得到瞬时正弦分量的幅值等。
(7)其他方面的一些应用,如对某些非直线和非稳定信号的测量值与处理结果的对比研究、在有风的情况下四周能量的测定、频带细分应用等。
鉴于此,提出一种基于优化Morlet小波的一维信号瞬态特征提取方法运行环境为MATLAB R2018A。程序测试了模拟信号,地震信号,发动机销子活塞故障振动信号,发动机气门正常振动信号,发动机排气门故障振动信号,结果如下。

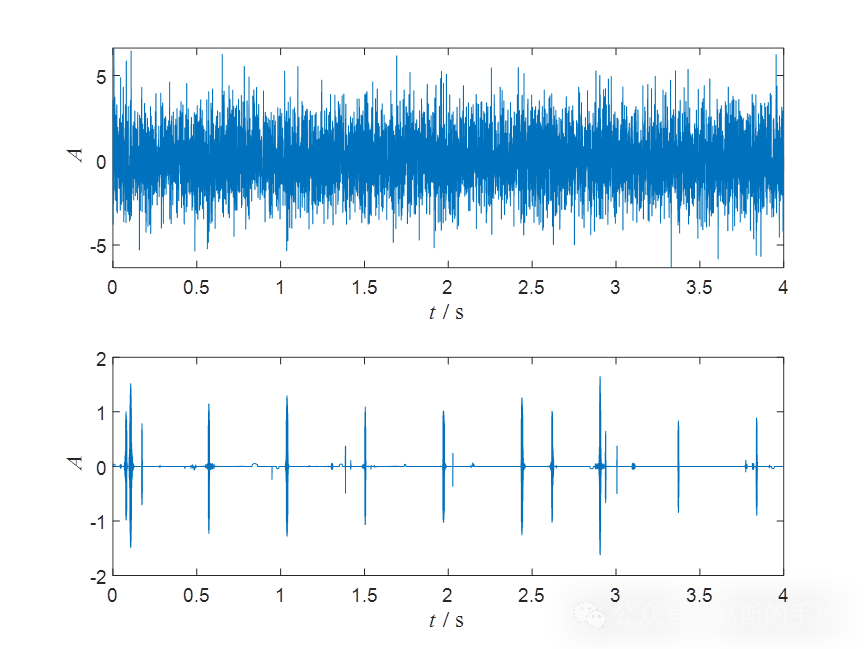
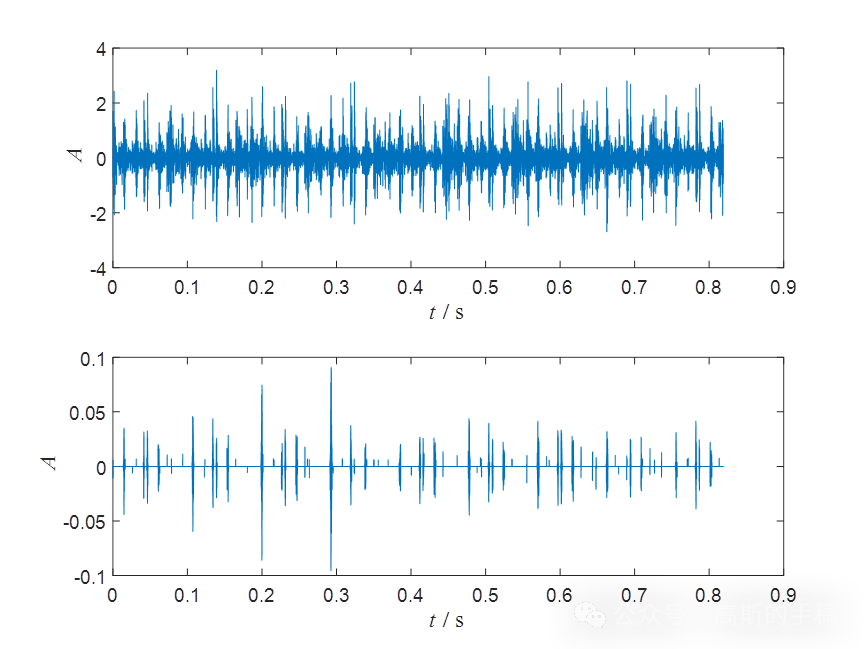
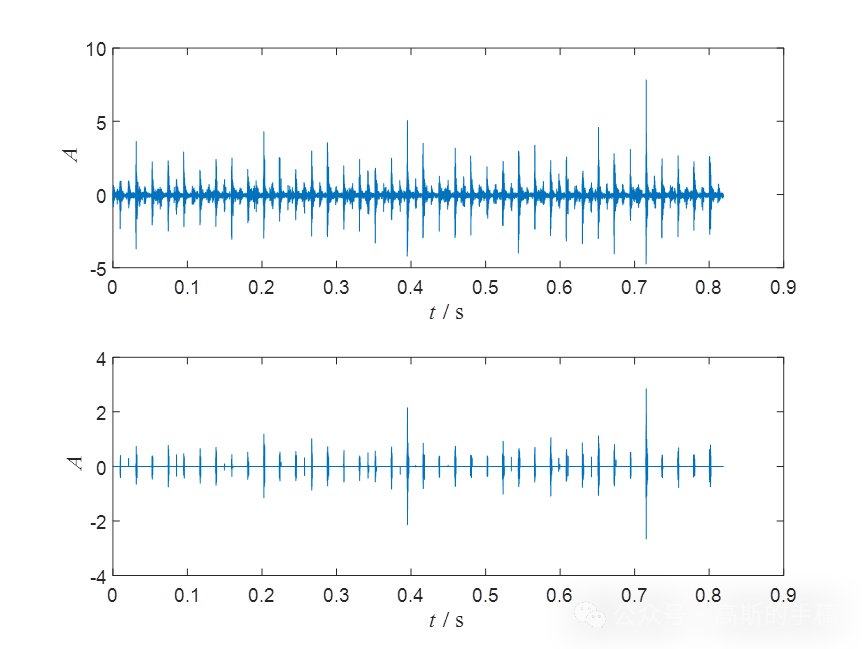

完整代码可通过知乎学术咨询获得。
工学博士,担任《Mechanical System and Signal Processing》《中国电机工程学报》《控制与决策》等期刊审稿专家,擅长领域:现代信号处理,机器学习,深度学习,数字孪生,时间序列分析,设备缺陷检测、设备异常检测、设备智能故障诊断与健康管理PHM等。