文章目录
- [1. 矩阵分解](#1. 矩阵分解)
- [2. S = Q Λ Q T S=Q\Lambda Q^T S=QΛQT](#2. S = Q Λ Q T S=Q\Lambda Q^T S=QΛQT)
- [3. A = U Σ V T A=U\Sigma V^T A=UΣVT](#3. A = U Σ V T A=U\Sigma V^T A=UΣVT)
- [4. A = LU 分解](#4. A = LU 分解)
- [5. 矩阵的四个子空间](#5. 矩阵的四个子空间)
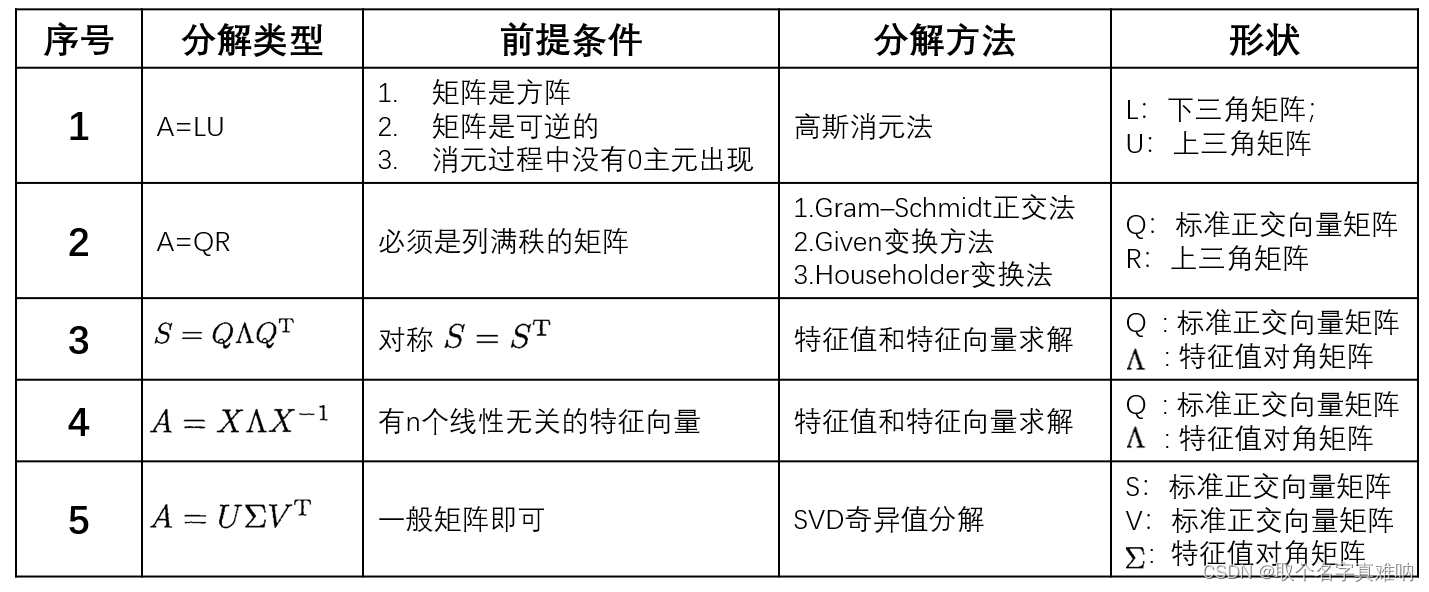
1. 矩阵分解
目前我们有很多重要的矩阵分解,每个分解对应于多个前提条件,分解方法,分解后的形状会中如下:
2. S = Q Λ Q T S=Q\Lambda Q^T S=QΛQT
当S为对称矩阵的时候,可以将S分解: S = Q Λ Q T S=Q\Lambda Q^T S=QΛQT,展开可得:
S = λ 1 q 1 q 1 T + λ 2 q 2 q 2 T + ⋯ λ n q n q n T \begin{equation} S=\lambda_1q_1q_1^T+\lambda_2q_2q_2^T+\cdots\lambda_nq_nq_n^T \end{equation} S=λ1q1q1T+λ2q2q2T+⋯λnqnqnT
- 两边乘以 q i q_i qi可得:
S q i = λ 1 q 1 q 1 T q i + λ 2 q 2 q 2 T + ⋯ + λ i q i q i T q i + ⋯ + λ n q n q n T q i ; q i T q i = 1 , q j T q i = 0 , i ≠ j \begin{equation} Sq_i=\lambda_1q_1q_1^Tq_i+\lambda_2q_2q_2^T+\cdots+\lambda_iq_iq_i^Tq_i+\cdots+\lambda_nq_nq_n^Tq_i;q_i^Tq_i=1,q_j^Tq_i=0,i\neq j \end{equation} Sqi=λ1q1q1Tqi+λ2q2q2T+⋯+λiqiqiTqi+⋯+λnqnqnTqi;qiTqi=1,qjTqi=0,i=j
S q i = λ i q i → λ i = q i T S q i \begin{equation} Sq_i=\lambda_iq_i\rightarrow \lambda_i=q_i^TSq_i \end{equation} Sqi=λiqi→λi=qiTSqi
3. A = U Σ V T A=U\Sigma V^T A=UΣVT
奇异值分解可以对任何实数矩阵有效,这里面核心的有两点:
-
- 通过 A A T AA^T AAT来算 σ 2 \sigma^2 σ2时,我们需要对A的 σ \sigma σ的正负号进行验证.
-
- 我们需要了解U,V正交单位特征向量与A的四个子空间的关系:真神奇!!!

- 我们需要了解U,V正交单位特征向量与A的四个子空间的关系:真神奇!!!
4. A = LU 分解
假设我们有矩阵A,我们希望对其进行LU分解如下:
A = L U → [ 2 3 4 7 ] = [ 1 0 2 1 ] [ 2 3 0 1 ] \begin{equation} A=LU\rightarrow\begin{bmatrix} 2&3\\\\ 4&7 \end{bmatrix}=\begin{bmatrix} 1&0\\\\ 2&1 \end{bmatrix}\begin{bmatrix} 2&3\\\\ 0&1 \end{bmatrix} \end{equation} A=LU→ 2437 = 1201 2031
- 矩阵A分解为两个秩为1的矩阵相加:
2 3 4 7 \] = \[ 2 3 4 6 \] + \[ 0 0 0 1 \] = \[ 1 2 \] \[ 2 3 \] + \[ 0 1 \] \[ 0 1 \] \\begin{equation} \\begin{bmatrix} 2\&3\\\\\\\\ 4\&7 \\end{bmatrix}=\\begin{bmatrix} 2\&3\\\\\\\\ 4\&6 \\end{bmatrix}+\\begin{bmatrix} 0\&0\\\\\\\\ 0\&1 \\end{bmatrix}=\\begin{bmatrix}1\\\\\\\\2\\end{bmatrix}\\begin{bmatrix}2\&3\\end{bmatrix}+\\begin{bmatrix}0\\\\\\\\1\\end{bmatrix}\\begin{bmatrix}0\&1\\end{bmatrix} \\end{equation} 2437 = 2436 + 0001 = 12 \[23\]+ 01 \[01
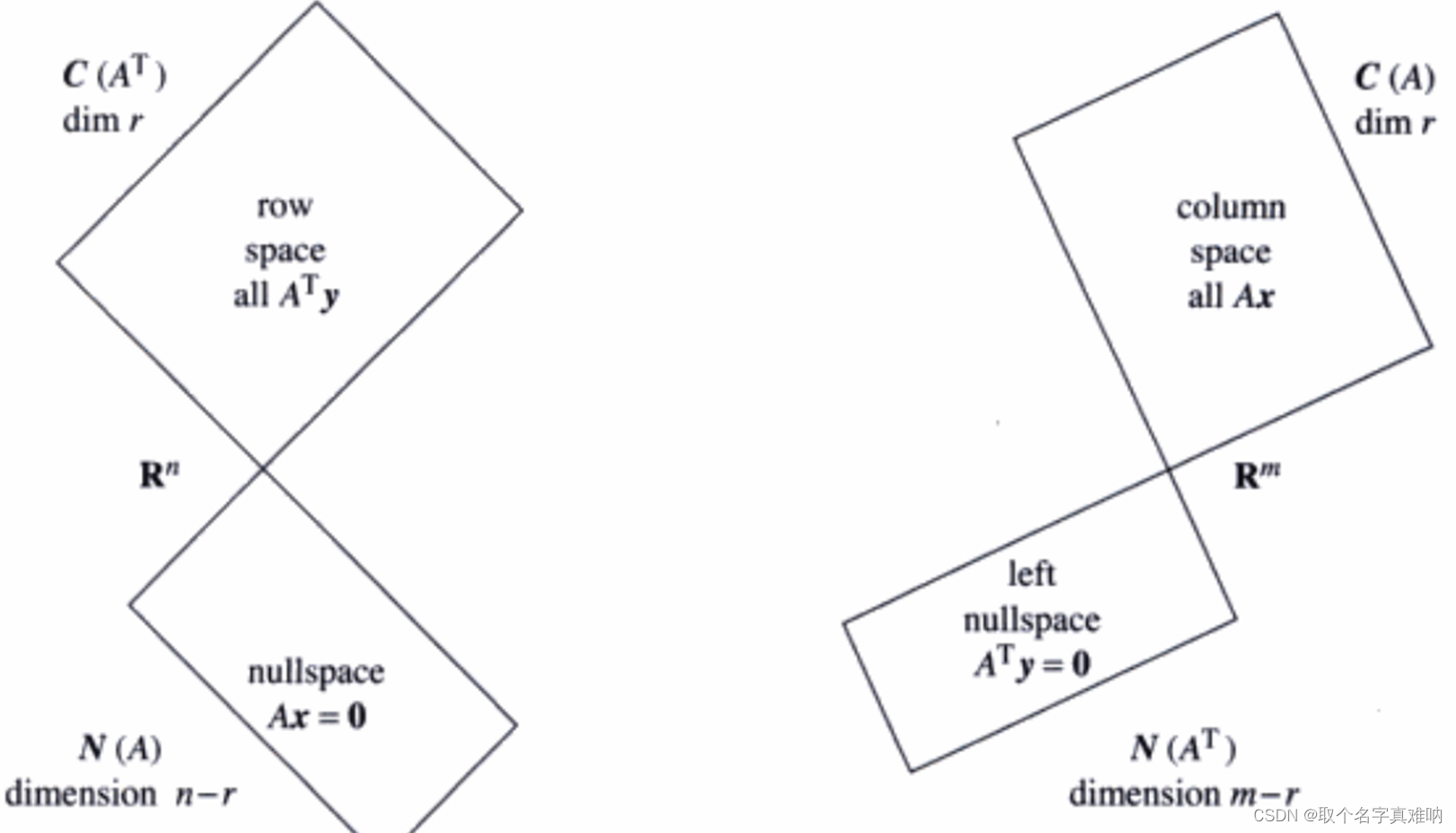
5. 矩阵的四个子空间
我们知道,对于一个m 行 n 列的矩阵A来说,根据列和行来说,分成4个空间,
- C ( A ) C(A) C(A)列空间(
columns space),维度为 R m R^m Rm - C ( A T ) C(A^T) C(AT)行空间(
rows space),维度为 R n R^n Rn - N ( A ) N(A) N(A)零空间(
rows space),维度为 R n R^n Rn - N ( A T ) N(A^T) N(AT)左零空间(
rows space),维度为 R m R^m Rm
四个子空间的相互关系如下: