归并排序法是典型的分治算法应用,1946年由冯.诺伊曼发明。
**算法思路:**归并排序算法有两个基本操作,一是分,也就是把原数组划分成两个子数组的过程,另一个是治,它将两个有序数组合并成一个更大的有序数组。
图解算法:分而治之
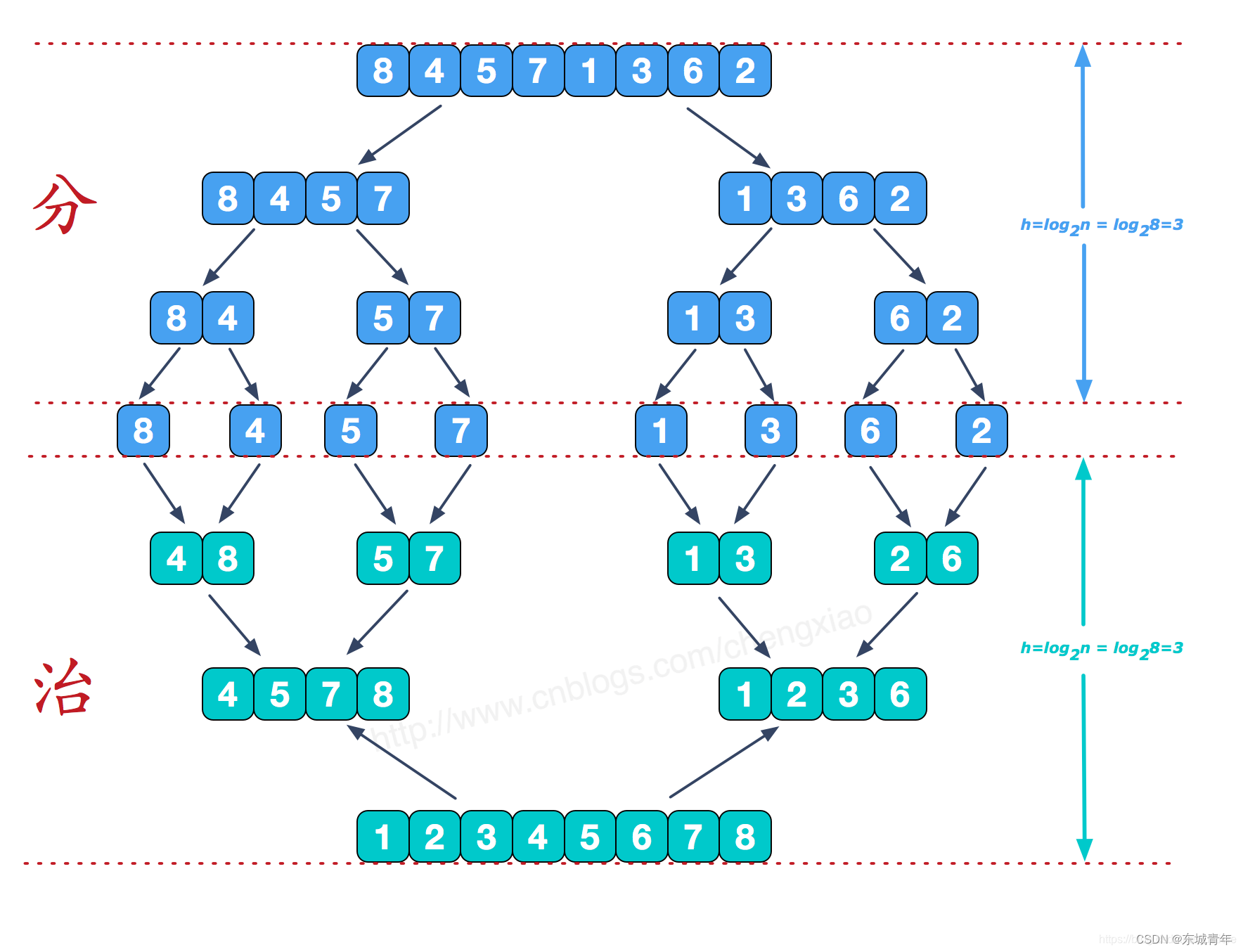
合并两个有序数组流程
我们需要将两个已经有序的子序列合并成一个有序序列,比如上图中的最后一次合并,要将[4,5,7,8]和[1,2,3,6]两个已经有序的子序列,合并为最终序列[1,2,3,4,5,6,7,8],来看下实现步骤。
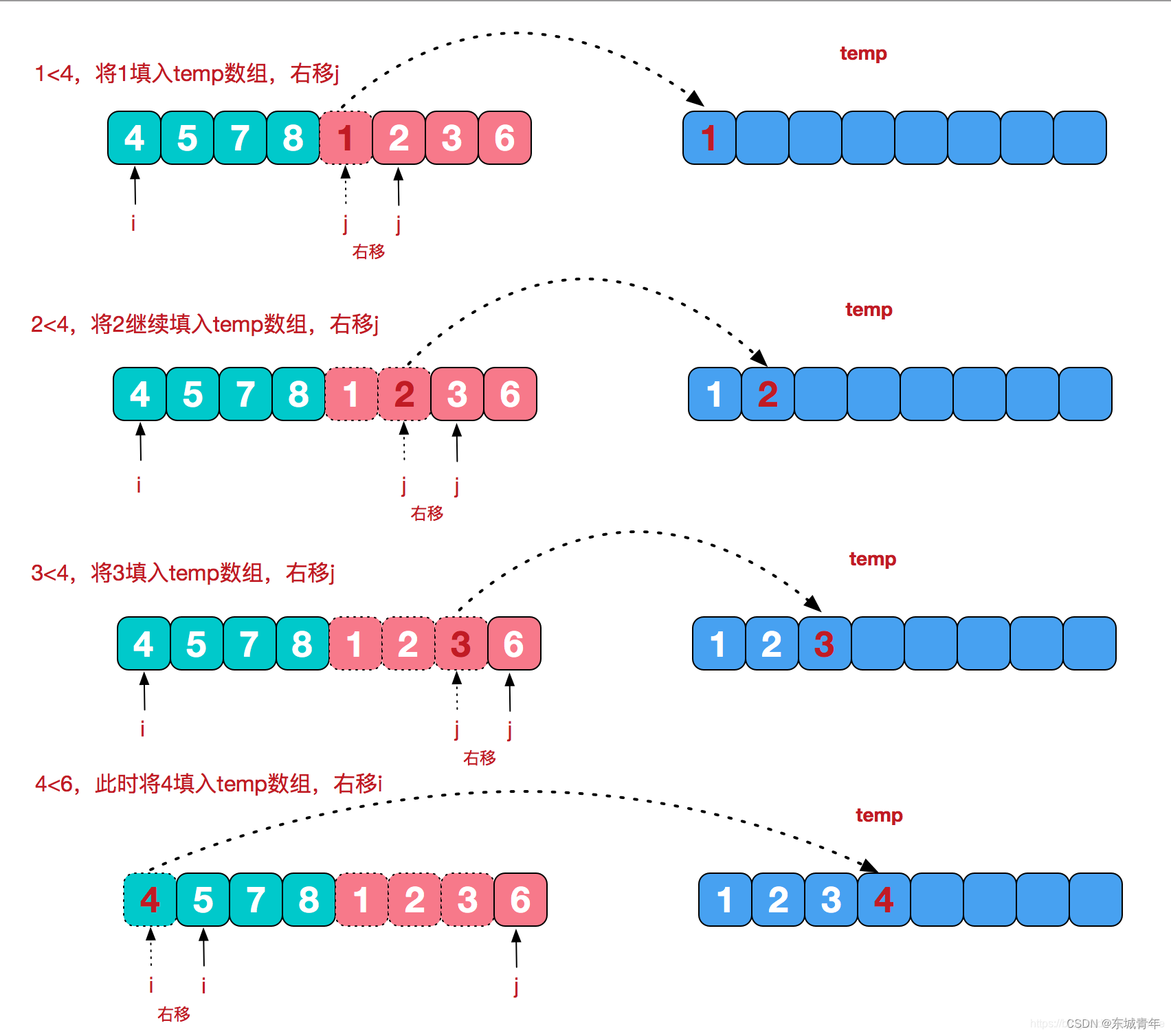
时间复杂度 O(Nlog(N))。
空间复杂度O(N):需要一个与原数组相同长度的数组做辅助来排序。
代码实现:
cpp
void Merge(int arr[], int tmpArr[], int left, int mid, int right)
{
// 标记左半区第一个元素
int l_pos = left;
// 标记右半区第一个元素
int r_pos = mid + 1;
// 临时数组元素下标
int pos = left;
// 合并
while (l_pos <= mid && r_pos <= right) {
if (arr[l_pos] < arr[r_pos]) {
tmpArr[pos++] = arr[l_pos++];
}
else {
tmpArr[pos++] = arr[r_pos++];
}
}
// 合并左半区剩余元素
while (l_pos <= mid) {
tmpArr[pos++] = arr[l_pos++];
}
// 合并右半区剩余元素
while (r_pos <= right) {
tmpArr[pos++] = arr[r_pos++];
}
// 把临时数组中合并后的元素复制回原来数组
while (left <= right) {
arr[left] = tmpArr[left];
left++;
}
}
void MergeSort(int arr[], int tmpArr[], int left, int right)
{
// 找中间点
int mid = (left + right) / 2;
if (left < right) {
// 递归划分左半区
MergeSort(arr, tmpArr, 0, mid);
// 递归划分右半区
MergeSort(arr, tmpArr, mid + 1, right);
// 合并已经排序的部分
Merge(arr, tmpArr, left, mid, right);
}
}