库存管理III ---- 分治-快排

题目:

分析:

这道题本质上是一个topK问题, 我们能够想到三种解决办法
解法一: 排序
解法二: 堆
解法三: 快速选择排序, 时间复杂度最好, 而且题目要求返回的顺序不限, 所以这个方法最好
数组中的第K个最大元素 ---- 分治-快排-CSDN博客, 我们在这道题中学习了快速选择排序, 这道题要求的是返回第K大的元素, 而这道题要的是前K个小的元素, 我们想到, 找第K大的元素, K左边的元素一定是<=K, K右边的元素一定是>=K,但是是无序的, 与这道题的要求恰好相同
那么我们想要前K小的元素, 只需要创建一个数组, 来存储K前面的元素即可, 所以这道题和上一道题其实是相同的, 这道题只是找第K小的元素
那么在后面的判断条件中, 我们还是设每一块区域元素个数为a,b,c
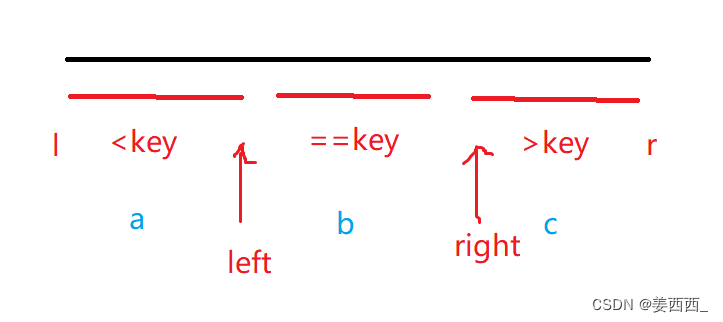
情况一: 如果第k个最小元素落在<key的区间, 说明此时a一定是>=k的, 此时只需要去[l, left]区间去找第k个最小元素即可
情况二: 如果第k个最小元素落在=key的区间, 那么b+c一定是>=k的, 此时只需要返回key即可, 因为这个区间都是key
情况三: 如果不是上述两种情况, 那么第k个最小元素一定落在>key的区间, , 此时需要去[right, r]区间去找, 但是我们要找的是第k-b-c小的元素, 因为我们舍去了=key和<key的区间

代码:

java 复制代码

class Solution {
    public int[] inventoryManagement(int[] stock, int cnt) {
        qsort(stock, 0, stock.length - 1, cnt);
        int[] ret = new int[cnt];
        for (int i = 0; i < cnt; i++) {
            ret[i] = stock[i];
        }
        return ret;
    }

    public void qsort(int[] nums, int l, int r, int k) {
        if (l >= r)
            return;
        int left = l - 1;
        int right = r + 1;
        int i = l;
        int key = nums[new Random().nextInt(r - l + 1) + l];
        while (i < right) {
            if (nums[i] < key)
                swap(nums, i++, ++left);
            else if (nums[i] == key)
                i++;
            else
                swap(nums, i, --right);
        }
        int a = left - l + 1;
        int b = right - left - 1;
        if (a > k)
            qsort(nums, l, left, k);
        else if (a + b >= k)
            return;
        else
            qsort(nums, right, r, k - a - b);
    }

    public void swap(int[] nums, int i, int j) {
        int tmp = nums[i];
        nums[i] = nums[j];
        nums[j] = tmp;
    }
}