165.二叉树：对称二叉树（力扣）

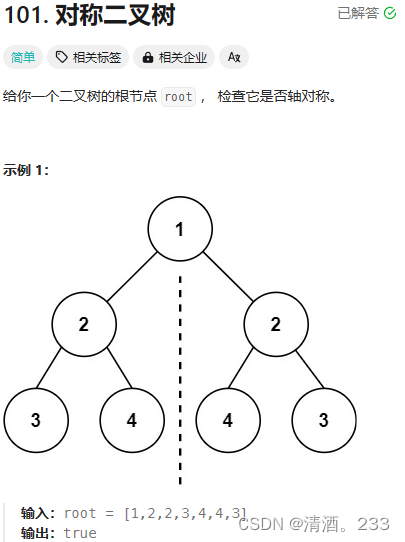
代码解决

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool compare(TreeNode* left, TreeNode* right)
    {
        // 两个子节点都为空，说明是对称的
        if (left == nullptr && right == nullptr) return true;
        // 只有一个子节点为空，说明不对称
        if (left == nullptr || right == nullptr) return false;
        // 两个子节点的值不相等，说明不对称
        if (left->val != right->val) return false;

        // 递归比较外侧和内侧节点
        bool outside = compare(left->left, right->right);
        bool inside = compare(left->right, right->left);

        // 只有外侧和内侧都对称，整个树才对称
        return outside && inside;
    }

    bool isSymmetric(TreeNode* root) 
    {
        // 空树是对称的
        if (root == nullptr) return true;
        // 检查左右子树是否对称
        return compare(root->left, root->right);
    }
};

1. 定义一个比较函数 compare，它接受两个 TreeNode* 类型的参数，代表要比较的两个子节点。
2. 在 compare 函数中，首先检查两个子节点是否都为空，如果是，则返回 true。
3. 如果只有一个子节点为空，则返回 false。
4. 如果两个子节点的值不相等，则返回 false。
5. 递归地调用 compare 函数来比较外侧节点（左子节点的左子节点和右子节点的右子节点）和内侧节点（左子节点的右子节点和右子节点的左子节点）。
6. 如果外侧和内侧节点都对称，则返回 true，否则返回 false。
7. 在 isSymmetric 函数中，首先检查根节点是否为空，如果是，则返回 true。
8. 调用 compare 函数来比较根节点的左子树和右子树是否对称。

这个算法的时间复杂度是 O(n)，因为每个节点都会被访问一次，其中 n 是树中节点的数量。空间复杂度也是 O(n)，因为需要存储递归调用的栈。