用最直观的方式告诉你：什么是主成分分析PCA_哔哩哔哩_bilibili
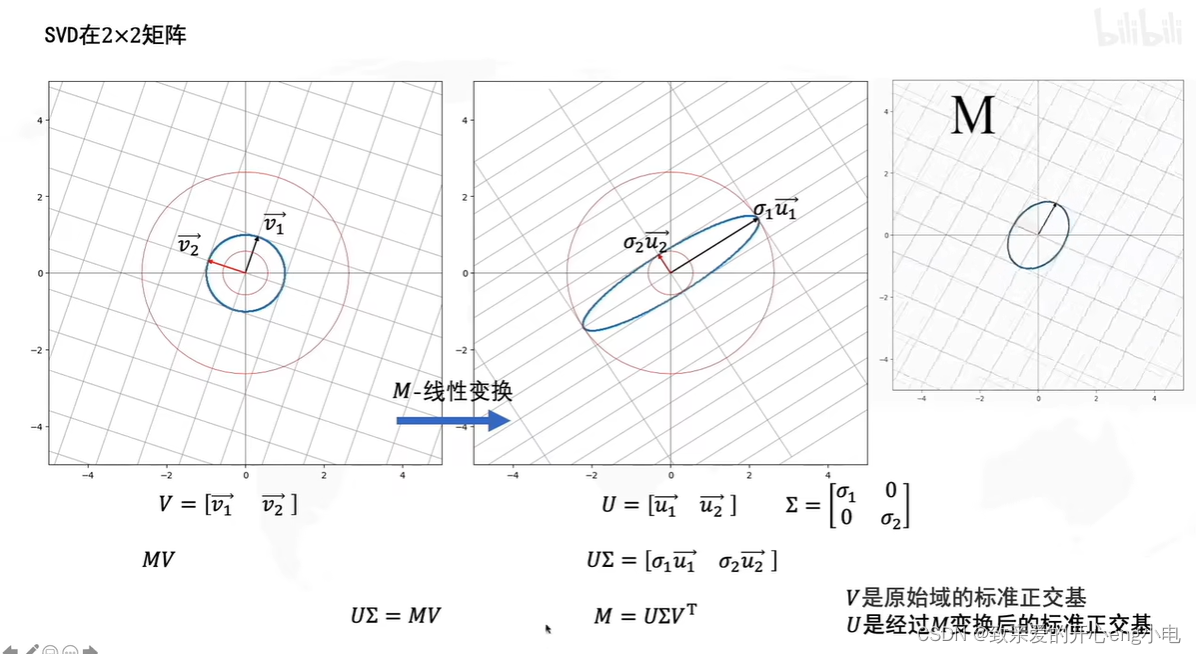
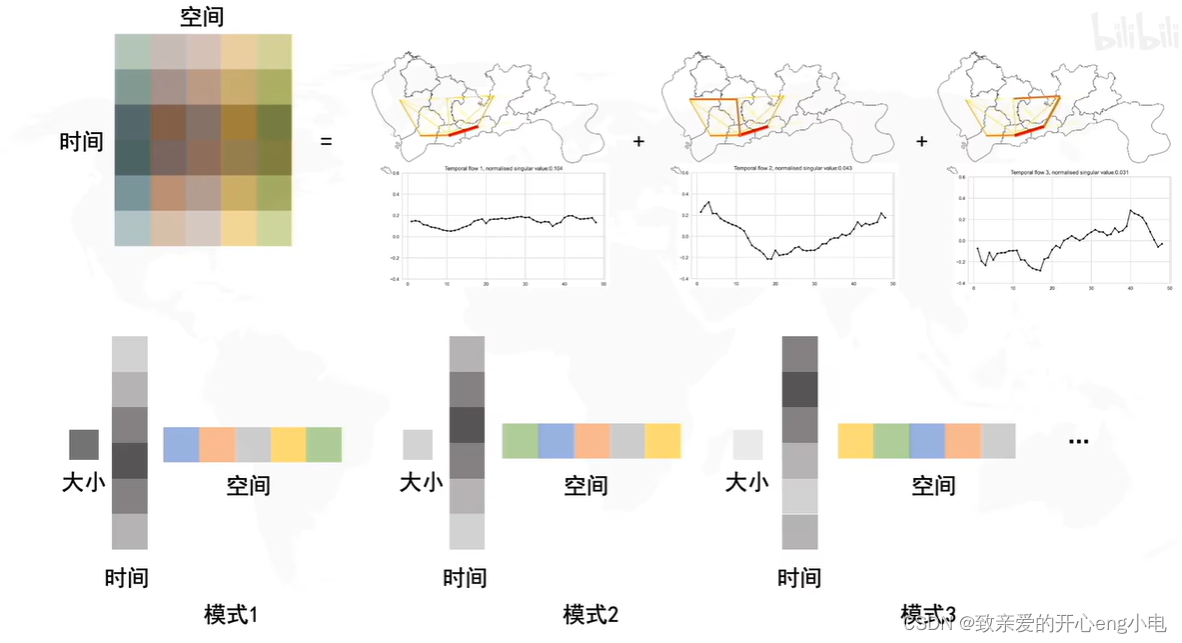
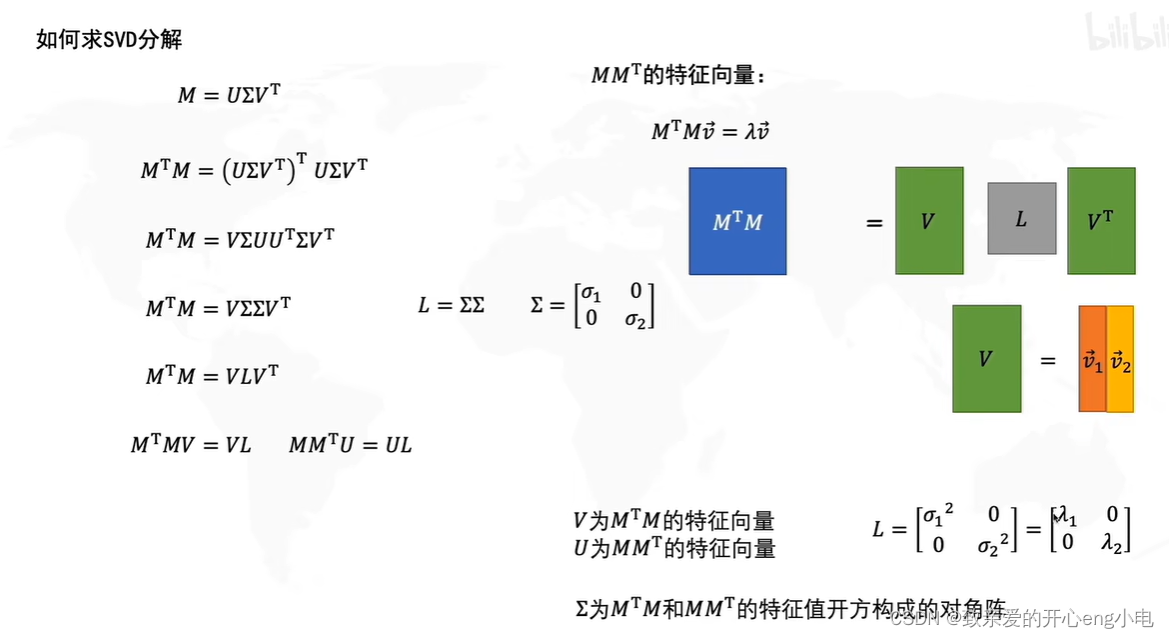
奇异值分解singular value decomposition，SVD
principal component analysis,PCA
降维操作
pca就是降维后使得信息损失最小
投影在坐标轴上的点越分散，信息保留越多
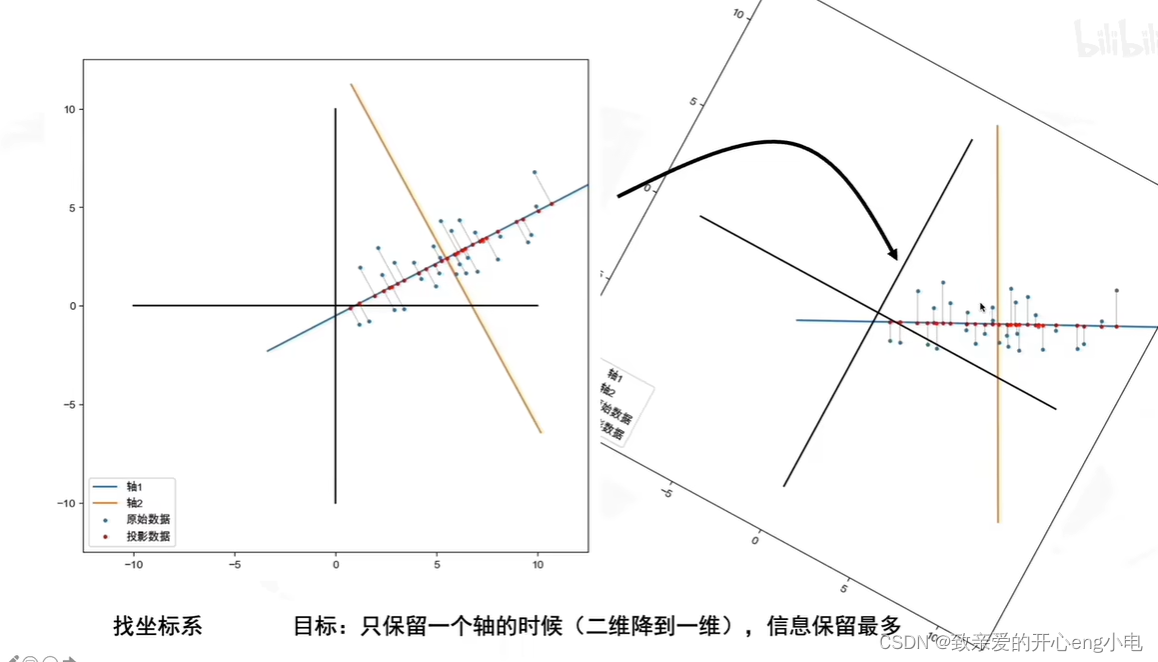
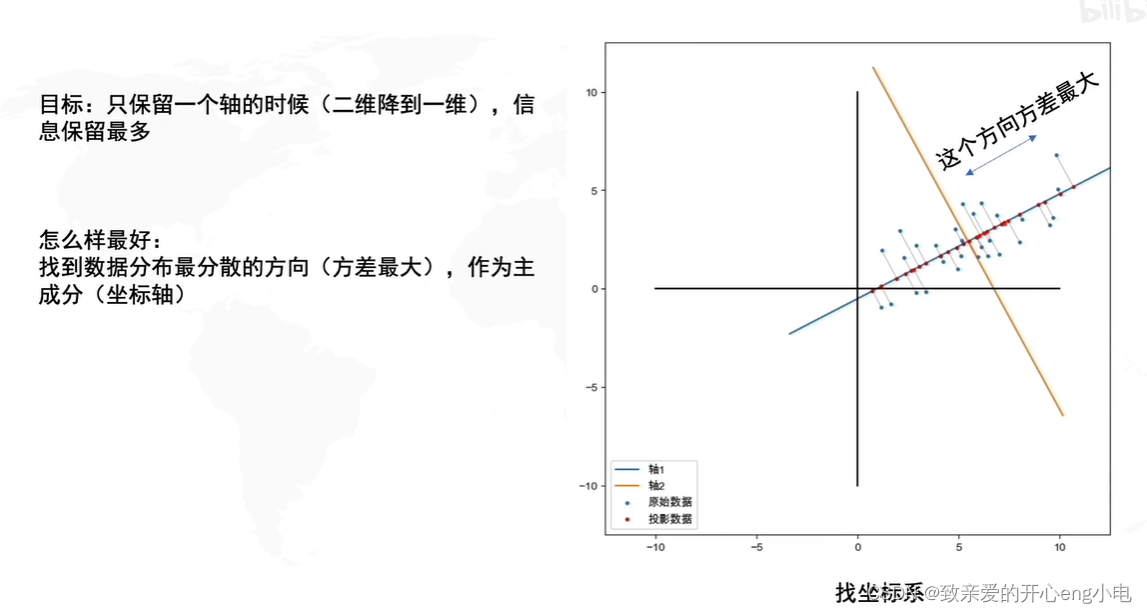
pca的实现
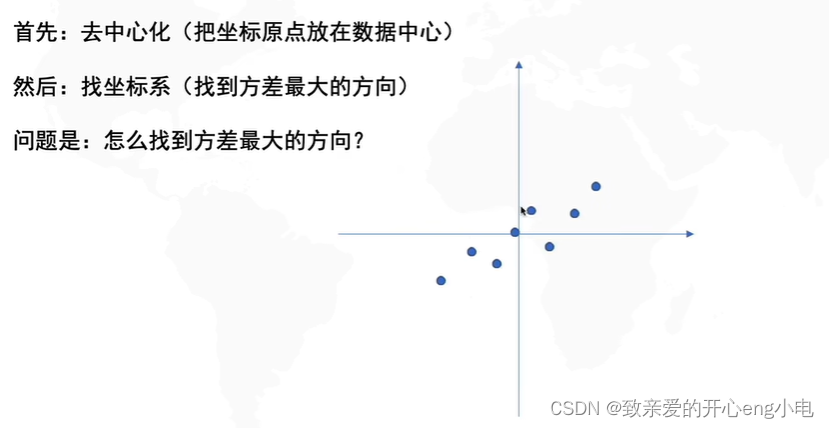
数据基本的线性变化
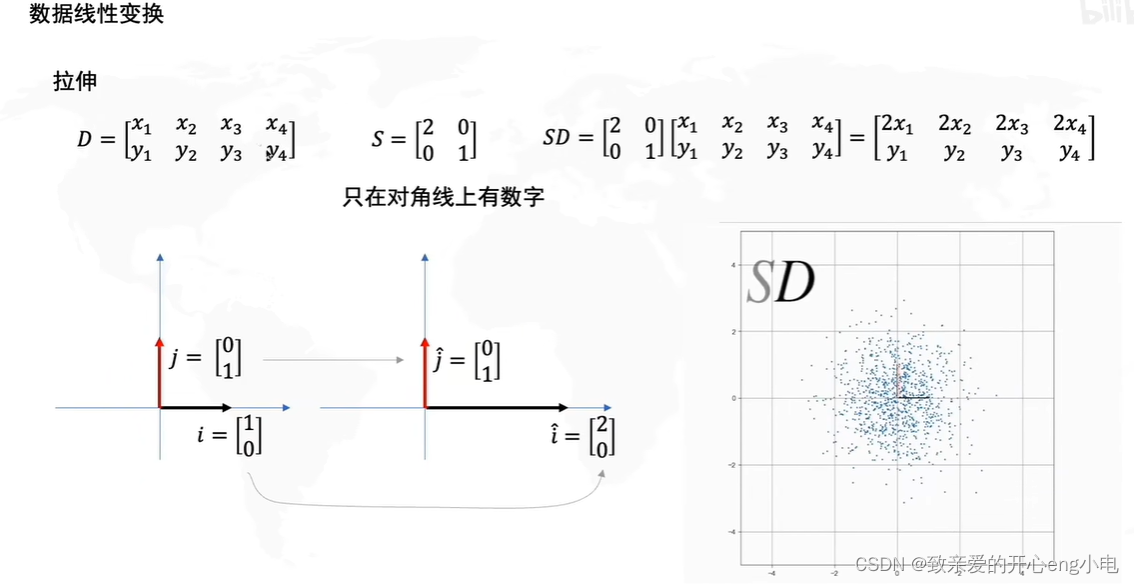
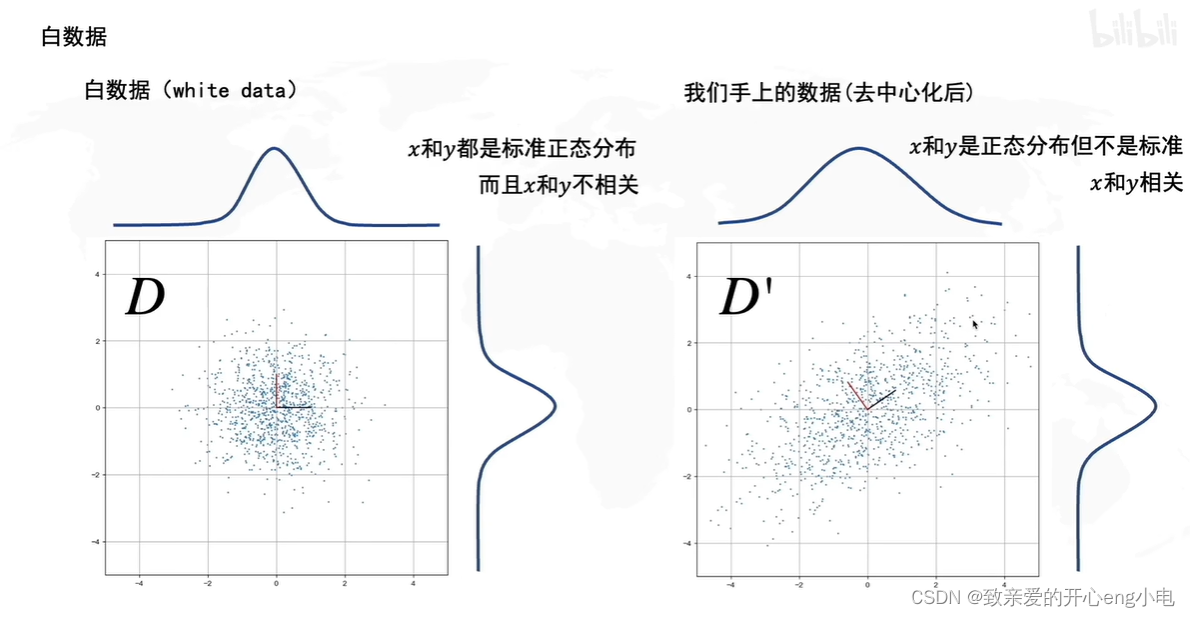
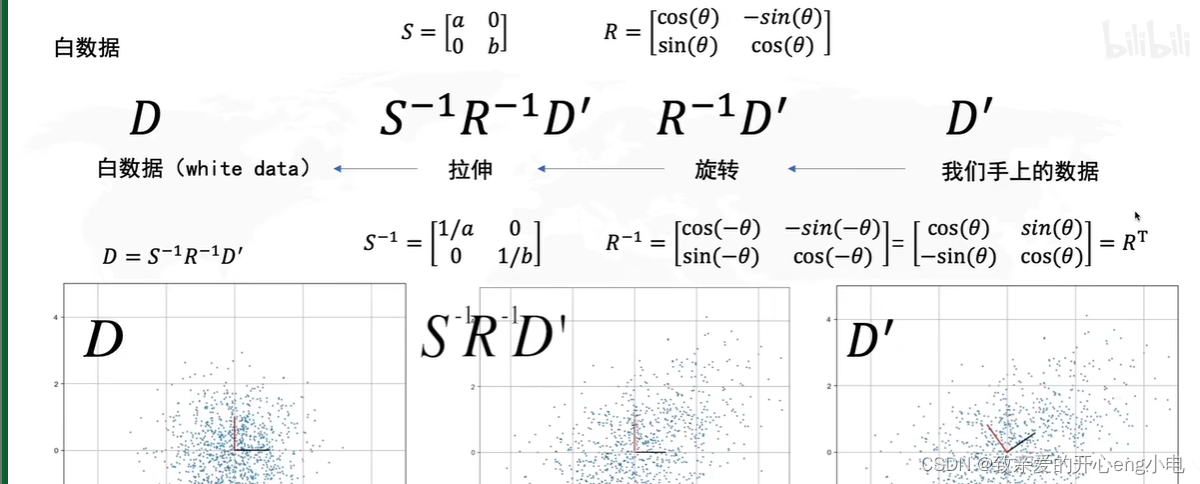
协方差矩阵的特征向量就是R
协方差
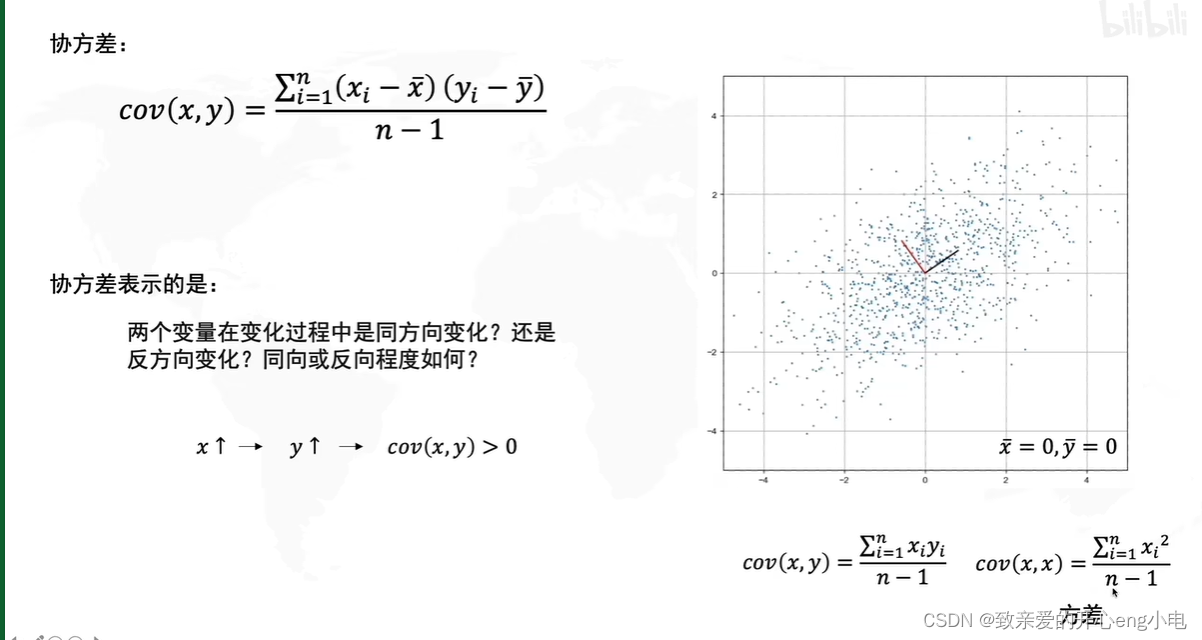
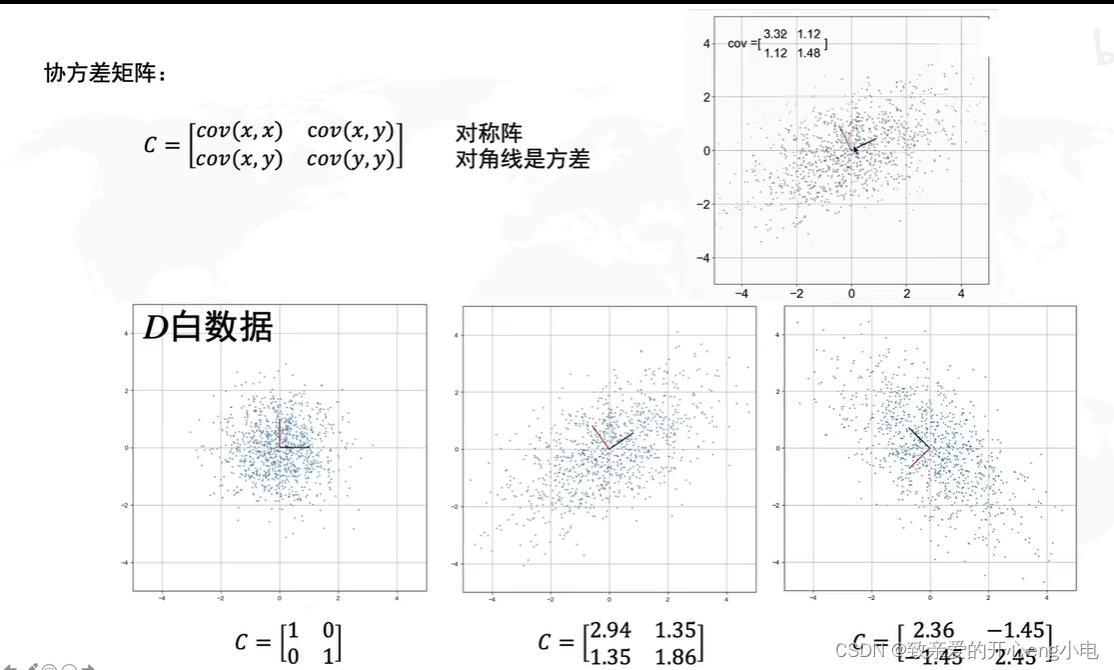
x，y正相关，协方差大于零；负相关，协方差小于零
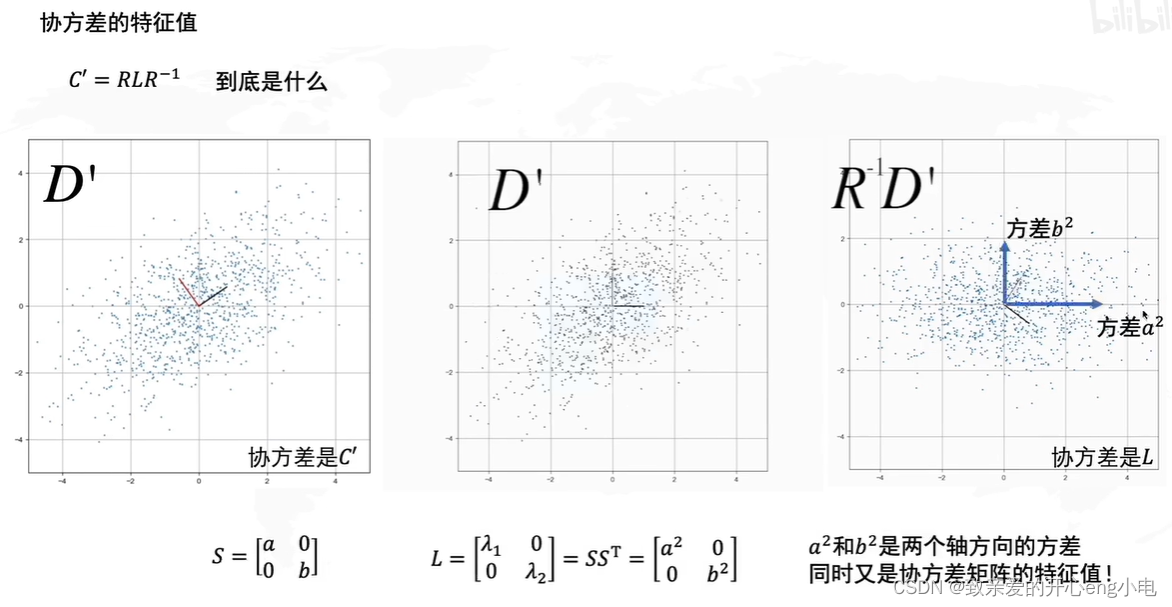
pca求解
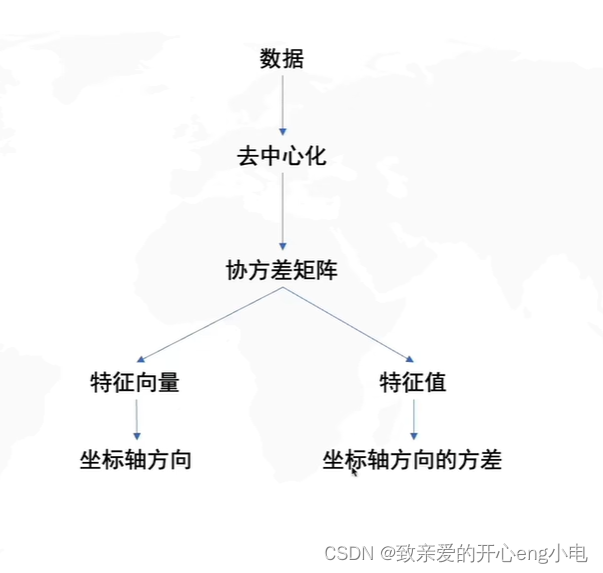
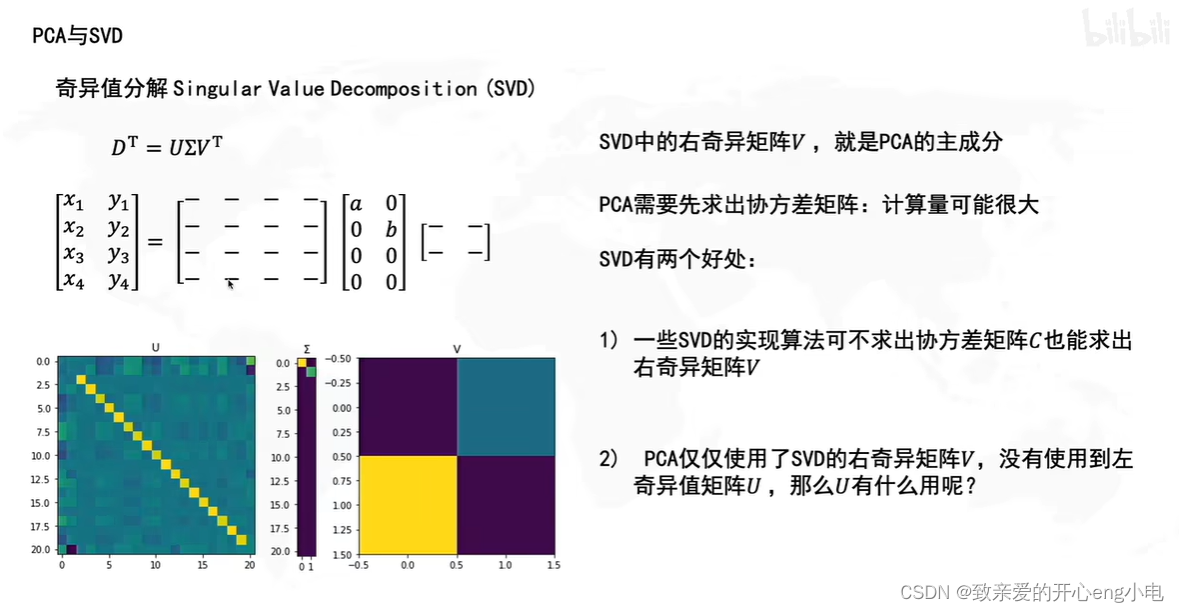
SVD中的V矩阵就是pca中的R
相关推荐
江瀚视野20 分钟前
Q3净利增长超预期，文心大模型调用量大增，百度未来如何分析？爱敲代码的憨仔26 分钟前
《线性代数的本质》陪学28 分钟前
百度遭初创企业指控抄袭，维权还是碰瓷？QCN_31 分钟前
湘潭大学人工智能考试复习1（软件工程）Landy_Jay32 分钟前
深度学习：GPT-1的MindSpore实践白光白光40 分钟前
量子神经网络全域观察1 小时前
如何复制只读模式下的腾讯文档panpantt3211 小时前
【参会邀请】第二届大数据与数据挖掘国际会议（BDDM 2024）邀您相聚江城！lindsayshuo1 小时前
jetson orin系列开发版安装cuda的gpu版本的opencv向阳逐梦1 小时前
ROS机器视觉入门：从基础到人脸识别与目标检测