往期文章推荐:
(一条神奇的分割线)
前言
好久没有更新的我总算在百忙之中抽出时间写了篇博客。
最近总算结束了动态规划的学习,真的是头昏脑涨啊。
最近也是开始了进制,链表和树的学习,让我们来详细看看吧!
(一条神奇的分割线)
进制
在日常生活中,我们用的都是十进制。
但是这个世界上不只有十进制,还有二进制、四进制、五进制、八进制、十六进制......
那么不同进制怎么转换呢?其实我们把其他进制转换成十进制就能做题了。
十进制转化成N进制:
用十进制数依次除以N,余数依次排列,最后除到不能再除,把余数倒着排列。
具体如下: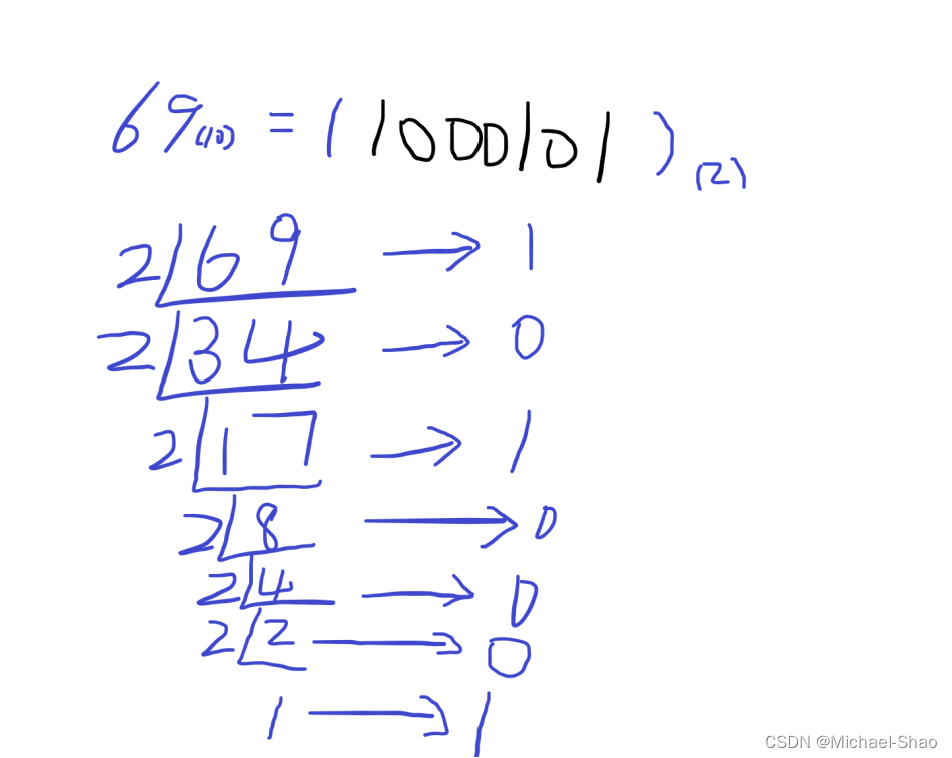
字不好看见谅......................................................................................
N进制转化成十进制:
从0开始,依次加当前数位上的数字乘N的第K-1次方(K代表当前数位)。
具体如下: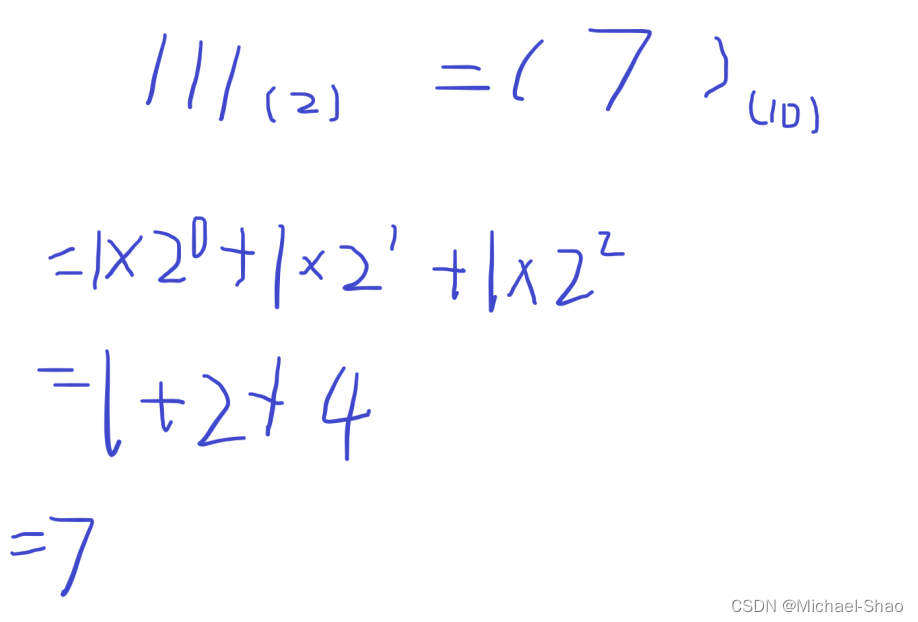
然后我们就可以解决不少关于进制加减的题目了。
补充一点位运算知识:
一张图讲明白。

与:两个必须都为真才为真
或 :一个为真即为真
非:两个都不为真即为真
异或:两个值不相同才为真
左移:在左边加上一个0
右移:删除左边的一个数
你学废了吗?
OK,去刷题吧!
关于进制就讲到这。
(一条神奇的分割线)
链表
链表是线性表的一种,线性表分为顺序表和链表两种实现方式。
顺序表可以理解为数组。
顺序表的优点是只需存放数据元素自身的信息;存储密度大;空间利用率高;存取速度快。
缺点则是需要实现分配存储空间;容易造成空间浪费(空间冗余);进行插入删除操作效率低。
顺序表就到这里!我们的主角是链表。
链表的概念:
用一组地址任意的储存单元(可以连续也可以不连续)依次储存线性表中的各个元素。
我们可以拿火车来做理解。(火车真的很像链表)
总结一下链表的优点:空间利用率高,插入删除操作便捷。
缺点:修改、查找麻烦。
链表的种类有单向链表、双向链表、循环链表。
单向链表:每个节点由两部分组成,元素自身信息即数据域(data),指向后继元素位置的信息称为指针域(link)。整个链表用list指出,以表明链表的首地址。链表为空时,list为null。
**双向链表:**除了数据域外有两个指针域,llink(左)指向前驱节点,rlink(右)指向后继节点。双向链表有循环线性和非循环线性。
**循环链表:**最后一个节点的指针指向链表的第一个链节点,整个链表形成一个循环,从表中任意节点出发均可找到表中其他节点。
在各位准备刷题之前记住一个坑点:有些节点被修改过了,所以后面的分析中要小心。
OK,在题海中漂泊吧!
关于链表就讲到这。
(一条神奇的分割线)
树
树可能是这三个里面最容易理解的了。
定义:树作为一种非线性的数据结构,是由n(≥0)个节点组成的有限集合。
如果n=0,那么这棵树为空树。
如果n>0,那么这棵树有个特定节点------根节点。说白了根节点就是所有节点的祖先。
根节点只有后继(儿子),没有前驱(父亲)。
接下来讲几个概念:
树的度:节点拥有子树的数量叫做节点的度,度为0的节点叫做叶节点。度不为0的节点叫做分支节点。树的度为这棵树中所有节点的度的最大值,就可以叫做几叉树。比如二叉树,就是每个节点的子树和子节点最多有两个。
树的前驱和后继:这个节点的父亲节点(很通俗)就是这个节点的前驱,每个节点的子节点就是这个节点的后继。节点孩子的孩子称为节点的孙子,节点成为子孙的祖先,同一个双亲的子节点之间互称兄弟。
树中节点的层次:树中根节点为第一层,根节点的孩子为第二层,以此类推。树中节点的最大层次成为树的深度或高度。
森林:n棵互不相交的树组成的集合叫森林。
然后我们讲一下树的性质:
1,除根节点没有父亲之外,其他节点有且仅有一个父亲。
2,n个节点的数,有且仅有n-1条边。
3,树中任意两个节点之间有且仅有一条简单路径。
OK,树就讲完了。
但是!
Wait a moment!
树中最精彩的部分才刚开始讲!
(一条神奇的分割线)
二叉树
二叉树其实是树的一种,但是它实在是太牛皮了,所以我要单独提溜出来讲。
二叉树是一种度数为2的数,就是每个节点的子节点最多有两个。每个节点的子节点分别称为左孩子,右孩子。两颗子树分别称为左子树,右子树。
鄙人目前只学到二叉树的遍历,就先讲到此处。
二叉树有四种遍历方式:
先序遍历:遍历顺序:根节点>左节点>右节点,优先级同上。
中序遍历:遍历顺序:左节点>根节点>右节点,优先级同上。
后序遍历:遍历顺序:左节点>右节点>根节点,优先级同上。
层次遍历:每一层从左到右遍历。
做题技巧:如果遇见给出某几种遍历的结果让你画出这棵树,牢记:后序遍历找根节点,中序遍历找左右节点。
最后,注意优先级问题!
OK,在题目中度过美好的一天吧!
(一条神奇的分割线)
后记
参考文献:
信息学奥赛一本通 初赛真题解析,一本通信息学名师工作室编著,南京大学出版社出版。
感谢阅览!烦请一键三连!Thanks♪(・ω・)ノ