找往期文章包括但不限于本期文章中不懂的知识点:
个人主页: 我要学编程(ಥ_ಥ)-CSDN博客
所属专栏:数据结构(Java版)
目录
[118. 杨辉三角](#118. 杨辉三角)
接上篇:数据结构之ArrayList与顺序表(上)-CSDN博客
ArrayList的具体使用
118. 杨辉三角
给定一个非负整数
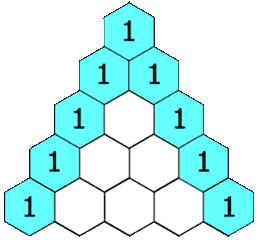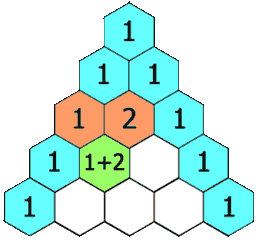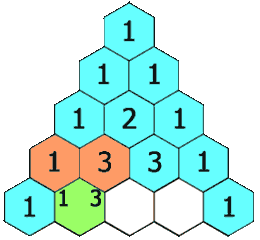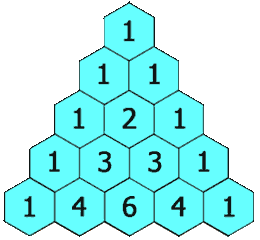
numRows, 生成「杨辉三角」的前 *numRows*行。在「杨辉三角」中,每个数是它左上方和右上方的数的和。
示例 1:
输入: numRows = 5 输出: [[1],[1,1],[1,2,1],[1,3,3,1],[1,4,6,4,1]]示例 2:
输入: numRows = 1 输出: [[1]]
1 <= numRows <= 30
分析:首先是一个杨辉三角的问题,杨辉三角其实就是一个只有一半的二维数组。

java
public class Test {
public static void main(String[] args) {
// 打印杨辉三角
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
int count = 0;
// 创建一个n行n列的二维数组
int[][] array = new int[n][n];
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (i == j) {
array[i][j] = 1;
}else if (j == 0) {
array[i][j] = 1;
}else {
// 只有从第二行开始才会有下面的规律
if (i >= 2) {
array[i][j] = array[i-1][j] + array[i-1][j-1];
}
}
}
}
for (int[] x:array) {
for (int y:x) {
if (y != 0) {
System.out.print(y+" ");
}
}
System.out.println();
}
}
}打印结果:

注意:杨辉三角还有一个规律就是第 i-1 行有 i 个元素。
这里主要的难点是:List<List<Integer>> 这个代码的意思是什么?分开看,List<Integer> 这个代码的意思是有一个线性表,这个线性表中存放的是 Integer 类型。List<List<Integer>> 难道这个代码的意思是有一个线性表,这个线性表里面存放的是一个线性表?没错!不过这个不叫线性表了。如果我们把这个List看成一个数组,那就是一个数组里面存放的是一个一个的数组元素,然后这些数组元素里面的元素是一个一个的整形包装类。这就是二维数组嘛!二维数组里面是一个一个的一维数组,而一维数组里面是一个一个的整型元素。
例如:
java
public class Test {
public static void main(String[] args) {
// 二维数组
// 根据顺序表的特点这个二维数组为0行0列
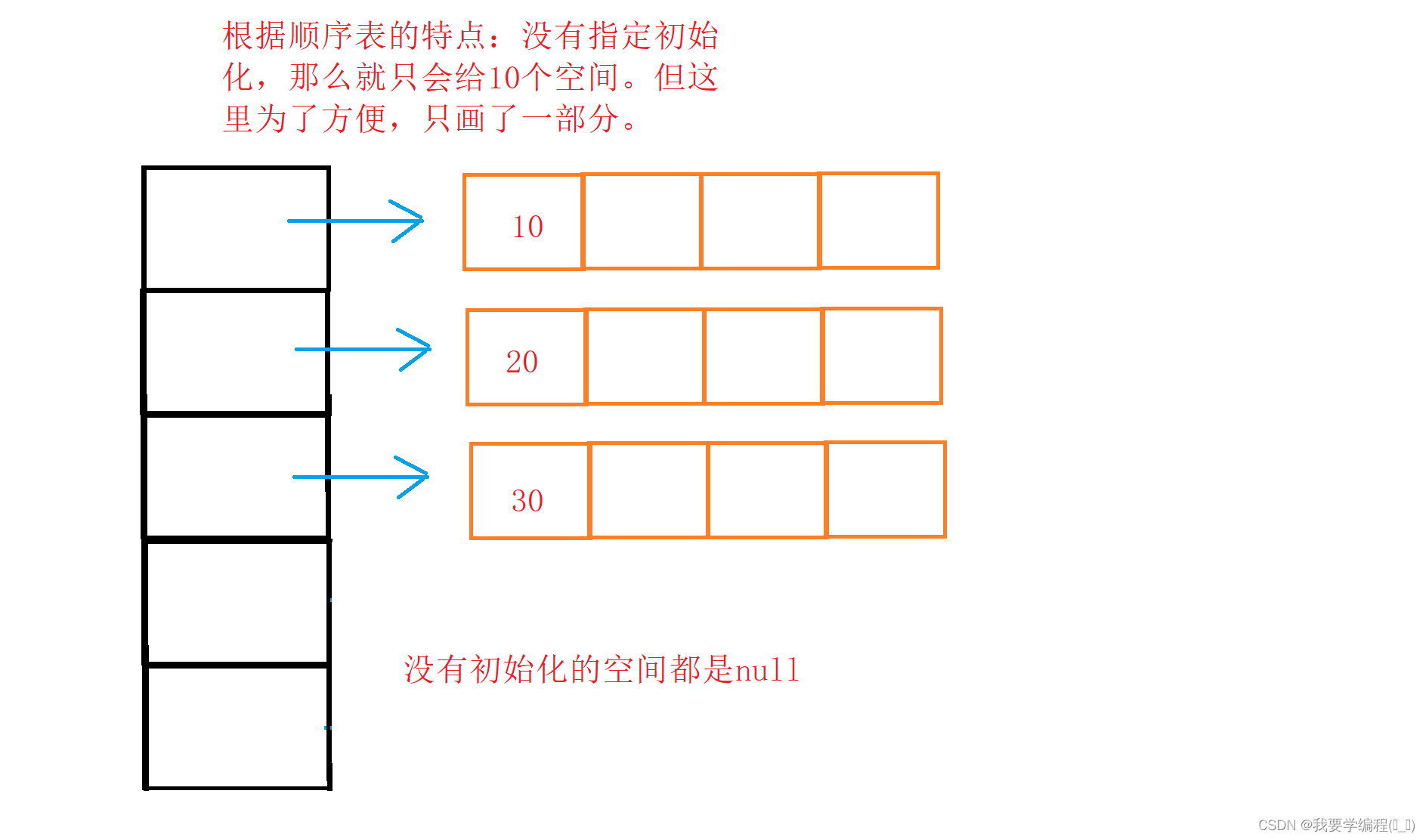
List<List<Integer>> list = new ArrayList<>();
//二维数组的初始化
list.add(new ArrayList<>()); // 二维数组的元素是一维数组
list.add(new ArrayList<>()); // 二维数组的元素是一维数组
list.add(new ArrayList<>()); // 二维数组的元素是一维数组
// 一维数组的初始化
list.get(0).add(10); // list.get(0)得到的是下标为0的一维数组,接着尾插10
list.get(1).add(20); // list.get(1)得到的是下标为1的一维数组,接着尾插20
list.get(2).add(30); // list.get(2)得到的是下标为2的一维数组,接着尾插30
}
}画图理解:
上面搞懂了,就可以开始做题了。这个题目的意思就是让我们把存放杨辉三角二维数组改成一个ArrayList。
根据我们用二维数组做题时的代码改编一下就可以了。
下面是改编的代码:
方法一:
java
public class Test {
public static List<List<Integer>> generate(int numRows) {
// 创建一个二维数组
List<List<Integer>> list = new ArrayList<List<Integer>>();
for (int i = 0; i < numRows; i++) {
// 不用下标直接尾插也是可以的
list.add(i, new ArrayList<>());
}
// 开始为二维数组存放元素
for (int i = 0; i < numRows; i++) {
List<Integer> list1 = list.get(i);
// 注意这里j的条件
for (int j = 0; j <= i; j++) {
if (i == j) {
list1.add(1);
}else if (j == 0) {
list1.add(1);
}else if (i >= 2) {
// 实现这个代码:a[i][j] = a[i-1][j]+a[i-1][j-1];
// 得到i-1下标数组的j位置的值 得到i-1下标数组的j-1位置的值
// 这个写法有问题。就像:3 = 5
// list.get(i).get(j) = list.get(i-1).get(j) + list.get(i-1).get(j-1);
// 这个就是对上面的代码进行翻译一下
int t = list.get(i - 1).get(j) + list.get(i - 1).get(j - 1);
list1.add(j , t);
}
}
}
return list;
}
public static void main(String[] args) {
List<List<Integer>> listList = generate(5);
for (List<Integer> list : listList) {
for (Integer x : list) {
System.out.print(x+" ");
}
System.out.println();
}
}
}方法二:
java
public class TestDrive {
public static List<List<Integer>> generate(int numRows) {
// 创建一个二维数组
List<List<Integer>> list = new ArrayList<List<Integer>>();
for (int i = 0; i < numRows; i++) {
// 不用下标直接尾插也是可以的
list.add(i, new ArrayList<>());
// 为二维数组的每一位元素的初始化为0
for (int j = 0; j < numRows; j++) {
list.get(i).add(j,0);
}
}
// 开始为二维数组存放元素
for (int i = 0; i < numRows; i++) {
List<Integer> list1 = list.get(i);
// 注意这里的j和方法进行区别
for (int j = 0; j < numRows; j++) {
if (i == j) {
// 因为所有元素都有初始值了,所以这里就都是set而不是add
list1.set(j,1);
}else if (j == 0) {
list1.set(j,1);
}else if (i >= 2) {
int t = list.get(i - 1).get(j) + list.get(i - 1).get(j - 1);
list1.set(j , t);
}
}
}
return list;
}
public static void main(String[] args) {
List<List<Integer>> listList = generate(5);
for (List<Integer> list : listList) {
for (Integer x : list) {
if (x != 0) {
System.out.print(x+" ");
}
}
System.out.println();
}
}
}方法一与方法二的区别:
方法二就是完全对前面代码的改编。因为前面我们在创建一个二维数组的同时是进行了初始化的,所以这里的所有元素都是有初始值的。但我们用顺序表来创建二维数组的时候,如果没有初始化,那么其值就是null,这个是不能参与运算的。因此,我们要手动的置为0,这样就可以参与运算了,否则就会发生异常。
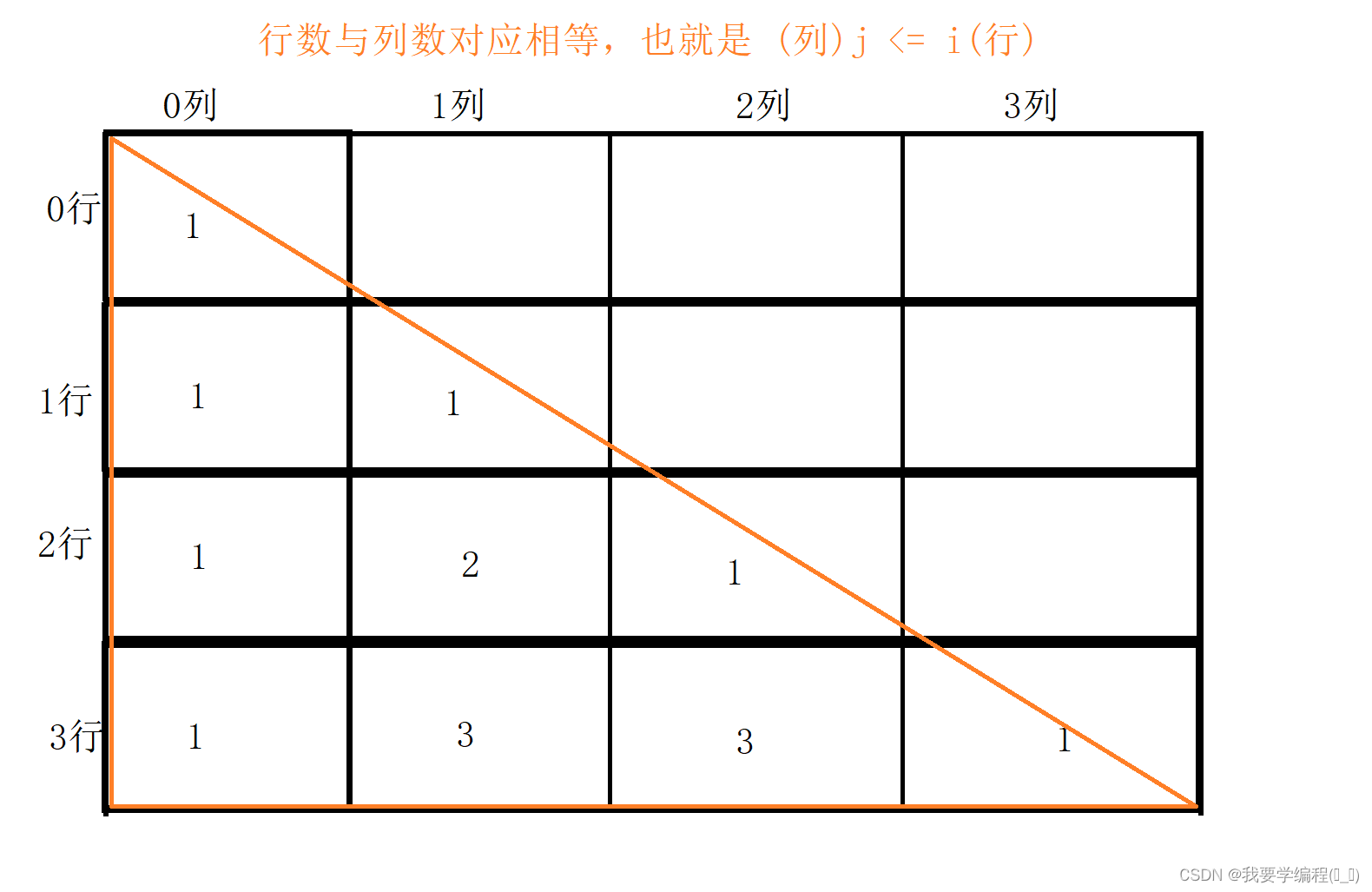
方法一就是改进了方法二的不足之处。既然你不初始化,在运算时,会发生异常,那么我就把你的范围卡在只参与运算的部分。也就是 j <= i 。我们仔细观察会发现杨辉三角是一个等腰直角三角形。如下图:
杨辉三角练习完了,接下来,就要进入重磅戏了:扑克洗牌算法。
扑克洗牌算法
要求:
-
生成一副扑克牌。
-
并且把这副扑克牌打乱。
-
发给3个人,每人每轮发一张,总共发5轮。
一张一张的牌,一张牌包括牌面值和花色
java
// 一张牌
public class Card {
public int rank; // 牌面值
public String suit; // 对应的花色
public Card(int rank, String suit) {
this.rank = rank;
this.suit = suit;
}
@Override
public String toString() {
return ""+suit+rank+" ";
}
}有了一张一张的牌,就可以生成一副牌和存放牌的容器,也就是顺序表
java
public class Cards {
// 生成牌的四色
public static final String suit[] = {"♠","♣","♥","♦"};
public List<Card> cardList;
// 在new一个对象的时候,就会生成存储一副牌的数组
public Cards() {
this.cardList = new ArrayList<>();
}
// 生成一副牌
// 为了方便,这里的牌面值都用数字表示
public List<Card> generateCards() {
for (int i = 1; i <= 14; i++) {
int count = 0;
for (int j = 0; j < suit.length; j++) {
// 生成一张牌
Card card = new Card(i, suit[j]);
// 把牌存放到数组中
cardList.add(card);
if (i > 13 && count < 2) {
count++;
}
if (count == 2) {
break;
}
}
}
return cardList;
}
}接下来就是要开始洗牌了。
java
// 洗牌
public void shuffle() {
// 通过随机下标进行交换
Random random = new Random();
// i=0就是自己和自己交换了
for (int i = cardList.size()-1; i > 0; i--) {
// 生成[0,i)之间的值,也就是[0,i-1]
int index = random.nextInt(i);
swap(cardList, index, i);
}
}
private void swap(List<Card> cardList, int index, int i) {
// 交换index和i下标对应的数组元素
// int tmp = a; a = b; b = tmp;
Card tmp = cardList.get(i);
// 把i下标的值,改为index下标对应的值
cardList.set(i, cardList.get(index));
cardList.set(index, tmp);
}发牌
java
// 发牌
// 给3人发5轮牌,每人每轮发一张
public List<List<Card>> dealCards() {
// 创建一个二维数组
List<List<Card>> listList = new ArrayList<>();
for (int i = 0; i < 3; i++) {
listList.add(new ArrayList<>());
}
for (int i = 0; i < 5; i++) {
for (int j = 0; j < 3; j++) {
// 第j个人拿到第0下标的牌
listList.get(j).add(cardList.get(0)); // 假设从最上面开始拿
// 每拿一张就少一张
cardList.remove(0);
}
}
return listList;
}测试:
java
public class Test {
public static void main(String[] args) {
// 生成一副牌
Cards cards = new Cards();
List<Card> cardList = cards.generateCards();
System.out.println(cardList);
// 开始洗牌------将牌的顺序打乱
cards.shuffle();
System.out.println(cardList);
// 开始发牌
List<List<Card>> listList = cards.dealCards();
// 查看结果
int i = 1;
for (List<Card> list: listList) {
System.out.print("第"+i+"个人拿到的牌:");
for (Card x : list) {
System.out.print(x+" ");
}
i++;
System.out.println();
}
}
}好啦!本期 数据结构之ArrayList与顺序表(下)的学习就到此结束啦!我们下一期再一起学习吧!