定义
projective transform
相机成像模型如下,从世界坐标系中的点到图像中的映射关系由一个矩阵 M M M施加在齐次坐标上,即:
p = K [ R ∣ t ] P = M P p=K\left[\begin{array}{ll} R \ | \ t \end{array}\right] P=M P p=K[R ∣ t]P=MP
其中的投影矩阵为:
M ( 3 × 4 ) = [ f s x c ′ 0 a f y c ′ 0 0 1 ] [ 1 0 0 0 0 1 0 0 0 0 1 0 ] [ R 3 × 3 0 3 × 1 0 1 × 3 1 ] [ I 3 × 3 T 3 × 1 0 1 × 3 1 ] \underset{(3 \times 4)}{\mathbf{M}}=\left[\begin{array}{ccc} f & s & x_c^{\prime} \\ 0 & a f & y_c^{\prime} \\ 0 & 0 & 1 \end{array}\right]\left[\begin{array}{llll} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \end{array}\right]\left[\begin{array}{cc} \mathbf{R}{3 \times 3} & \mathbf{0}{3 \times 1} \\ \mathbf{0}{1 \times 3} & 1 \end{array}\right]\left[\begin{array}{cc} \mathbf{I}{3 \times 3} & \mathbf{T}{3 \times 1} \\ \mathbf{0}{1 \times 3} & 1 \end{array}\right] (3×4)M= f00saf0xc′yc′1 100010001000 [R3×301×303×11][I3×301×3T3×11]
依次是 intrinsics projection rotation translation,共有5+3+3= 11个自由度。
求解它需要求解 M M M的11个元素,这个一般用于相机外参和内参对准。
w ∗ u w ∗ v w \] = \[ m 11 m 12 m 13 m 14 m 21 m 22 m 23 m 24 m 31 m 32 m 33 m 34 \] \[ X Y Z 1 \] {\\left\[\\begin{array}{c} w\^\* u \\\\ w\^\* v \\\\ w \\end{array}\\right\]=\\left\[\\begin{array}{llll} m_{11} \& m_{12} \& m_{13} \& m_{14} \\\\ m_{21} \& m_{22} \& m_{23} \& m_{24} \\\\ m_{31} \& m_{32} \& m_{33} \& m_{34} \\end{array}\\right\]\\left\[\\begin{array}{c} X \\\\ Y \\\\ Z \\\\ 1 \\end{array}\\right\]} w∗uw∗vw = m11m21m31m12m22m32m13m23m33m14m24m34 XYZ1 对于每对点,uv坐标考虑之后都有2个方程: u i ( m 20 X i + m 21 Y i + m 22 Z i + m 23 ) = m 00 X i + m 01 Y i + m 02 Z i + m 03 v i ( m 20 X i + m 21 Y i + m 22 Z i + m 23 ) = m 10 X i + m 11 Y i + m 12 Z i + m 13 u_i\\left(m_{20} X_i+m_{21} Y_i+m_{22} Z_i+m_{23}\\right)=m_{00} X_i+m_{01} Y_i+m_{02} Z_i+m_{03} \\\\ v_i\\left(m_{20} X_i+m_{21} Y_i+m_{22} Z_i+m_{23}\\right)=m_{10} X_i+m_{11} Y_i+m_{12} Z_i+m_{13} ui(m20Xi+m21Yi+m22Zi+m23)=m00Xi+m01Yi+m02Zi+m03vi(m20Xi+m21Yi+m22Zi+m23)=m10Xi+m11Yi+m12Zi+m13 写成矩阵 \[ X i Y i Z i 1 0 0 0 0 − u i X i − u i Y i − u i Z i − u i 0 0 0 0 X i Y i Z i 1 − v i X i − v i Y i − v i Z i − v i \] \[ m 00 m 10 m 02 m 03 m 10 m 11 m 12 m 13 m 20 m 21 m 22 m 23 \] = \[ 0 0 \] \\left\[\\begin{array}{cccccccccccc} X_i \& Y_i \& Z_i \& 1 \& 0 \& 0 \& 0 \& 0 \& -u_i X_i \& -u_i Y_i \& -u_i Z_i \& -u_i \\\\ 0 \& 0 \& 0 \& 0 \& X_i \& Y_i \& Z_i \& 1 \& -v_i X_i \& -v_i Y_i \& -v_i Z_i \& -v_i \\end{array}\\right\] \\left\[ \\begin{array}{l} m_{00} \\\\ m_{10} \\\\ m_{02} \\\\ m_{03} \\\\ m_{10} \\\\ m_{11} \\\\ m_{12} \\\\ m_{13} \\\\ m_{20} \\\\ m_{21} \\\\ m_{22} \\\\ m_{23} \\end{array}\\right\] =\\left\[\\begin{array}{l} 0 \\\\ 0 \\end{array}\\right\] \[Xi0Yi0Zi0100Xi0Yi0Zi01−uiXi−viXi−uiYi−viYi−uiZi−viZi−ui−vi\] m00m10m02m03m10m11m12m13m20m21m22m23 =\[00
SVD(奇异值分解)是求解超定线性方程组和最小均方误差的最小二乘问题的首选方法.
Homography
单应矩阵Homography 描述的是从一个图像的像素到另一个图像的像素的变换,也就是Image to image projection。实际上就是下图这几种变换。
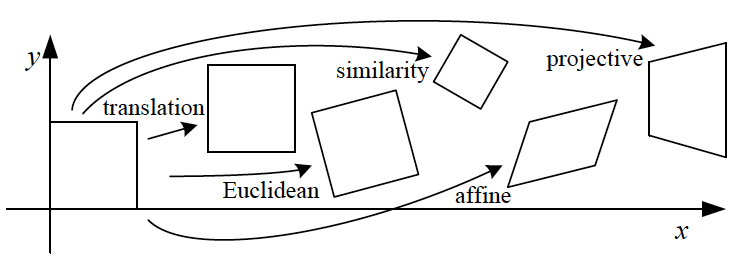
通常用于图像拼接,在图像拼接时成像点几乎没有变换,只有旋转引起的视角变化。
单应矩阵用4对点就可以求解,也就是确定上图中四边形在 I 1 I_1 I1和 I 2 I_2 I2的四个角。
Essential Matrix
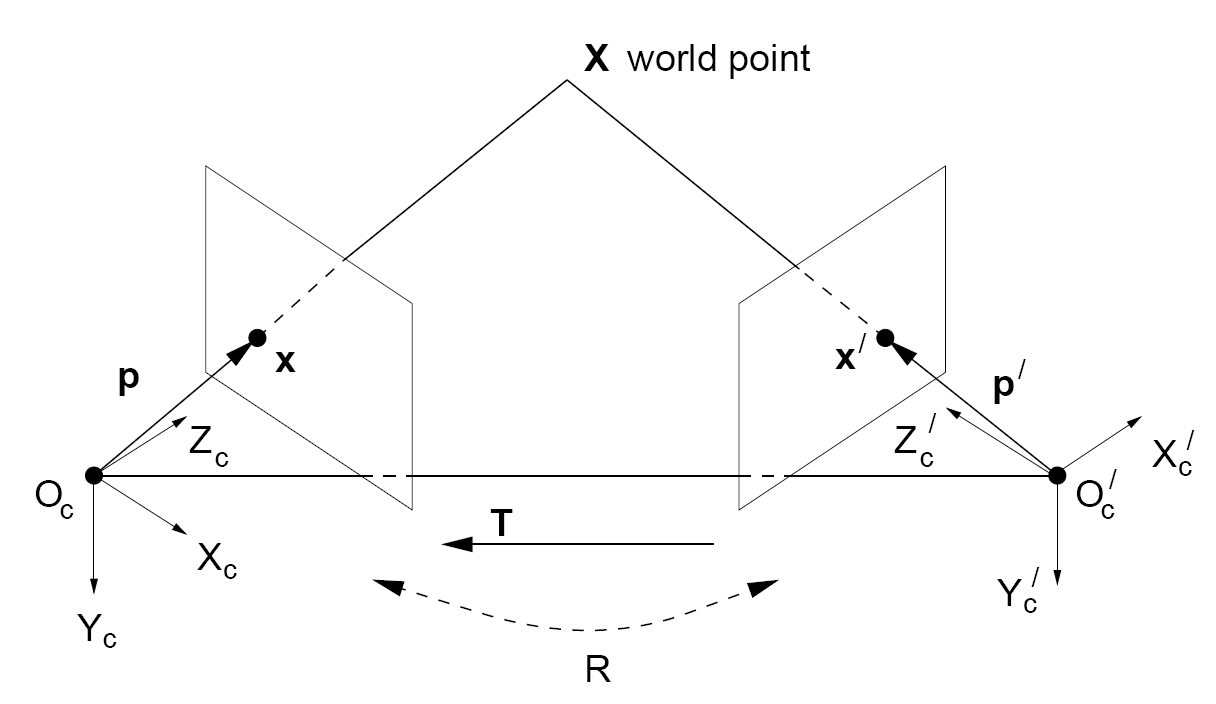
描述了两个相机坐标系,坐标点的坐标变换关系
p ′ = R p + T \mathbf{p}^{\prime}=\mathbf{R} \mathbf{p}+\mathbf{T} p′=Rp+T
左右同时乘以左右目之间的变换矩阵:
p ′ ⋅ ( [ T × ] R p ) = 0 E = [ T × ] R , p ′ T E p = 0 \mathbf{p}^{\prime} \cdot\left(\left[\mathrm{T}\times\right] \mathbf{R} \mathbf{p}\right)=0 \\ \mathbf{E}=\left[\mathrm{T}\times\right] \mathbf{R} \ , \ \mathbf{p}^{\prime^T} \mathbf{E} \mathbf{p}=0 p′⋅([T×]Rp)=0E=[T×]R , p′TEp=0
Fundamental matrix
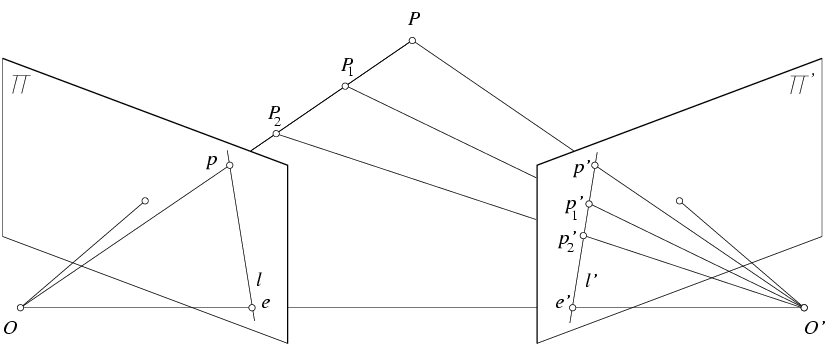
描述了两个相机相同3D点构成的像素坐标的几何约束关系。
p i m , r i g h t T F p i m , l e f t = 0 \mathbf{p}{i m, r i g h t}^{\mathrm{T}} \mathbf{F} \mathbf{p}{i m, l e f t}=0 pim,rightTFpim,left=0
对每一个两个成像平面上的匹配点对,投影变换把一个齐次坐标投影到另一个齐次坐标:
u ′ v ′ 1 \] \[ f 11 f 12 f 13 f 21 f 22 f 23 f 31 f 32 f 33 \] \[ u v 1 \] = 0 \\left\[\\begin{array}{lll} u\^{\\prime} \& v\^{\\prime} \& 1 \\end{array}\\right\]\\left\[\\begin{array}{lll} f_{11} \& f_{12} \& f_{13} \\\\ f_{21} \& f_{22} \& f_{23} \\\\ f_{31} \& f_{32} \& f_{33} \\end{array}\\right\]\\left\[\\begin{array}{l} u \\\\ v \\\\ 1 \\end{array}\\right\]=0 \[u′v′1\] f11f21f31f12f22f32f13f23f33 uv1 =0 于是可以写出8个(八点法)这样的方程: \[ u 1 ′ u 1 u 1 ′ v 1 u 1 ′ v 1 ′ u 1 v 1 ′ v 1 v 1 ′ u 1 v 1 1 \] \[ f 11 f 12 f 13 f 21 f 22 f 23 f 31 f 32 f 33 \] = 0 \\left\[\\begin{array}{llllllllll} u_1\^{\\prime} u_1 \& u_1\^{\\prime} v_1 \& u_1\^{\\prime} \& v_1\^{\\prime} u_1 \& v_1\^{\\prime} v_1 \& v_1\^{\\prime} \& u_1 \& v_1 \& 1 \\end{array}\\right\]\\left\[\\begin{array}{c} f_{11} \\\\ f_{12} \\\\ f_{13} \\\\ f_{21} \\\\ f_{22} \\\\ f_{23} \\\\ f_{31} \\\\ f_{32} \\\\ f_{33} \\end{array}\\right\]=\\mathbf{0} \[u1′u1u1′v1u1′v1′u1v1′v1v1′u1v11\] f11f12f13f21f22f23f31f32f33 =0  极线交于一点,上面八点法计算出的结果是错误的。 在考虑极线约束的情况下, F F F秩为2,需要在求解SVD分解时去除最小特征值。 ## SLAM中求解Homography矩阵、Essential矩阵和Fundamental矩阵的适用场合是什么 以下是这些矩阵的适用场合和作用: ### Homography矩阵 适用场合 * 平面场景:Homography矩阵适用于两幅图像中包含同一平面的情况,例如,地面、墙面等。 * 运动估计:在摄像机运动平行于图像平面时,Homography可以有效地估计相机的平移和旋转。 * 图像配准和拼接:在图像拼接、全景图生成中,Homography用于将两幅图像对齐。 * 姿态估计:在某些简单场景中,可以用Homography矩阵进行相机姿态估计。 **作用** * 图像变换:将一幅图像的坐标系映射到另一幅图像的坐标系。 * 特征点匹配:在已知平面场景中,通过Homography矩阵可以将特征点从一个视图映射到另一个视图。 ### Essential矩阵 适用场合 * 已校正相机:Essential矩阵适用于内部参数已知且经过校正的相机(内参矩阵K已知)。 * 相机位姿估计:用于估计相机的相对姿态(旋转和平移),特别是当场景是三维的时。 * 立体视觉:在双目立体视觉中,用于计算视差和重建3D结构。 **作用** 相机位姿估计:解出相对旋转和平移。 3D重建:通过求解Essential矩阵,可以进行三维点的重建。 ### Fundamental矩阵 适用场合 * 未校正相机:适用于内部参数未知或未校正的相机。 两视图几何:在任意两幅图像之间建立几何关系,无需相机内参。 * 特征点匹配约束:用于约束特征点匹配的搜索空间。 **作用** 极线约束:在未校正图像中,Fundamental矩阵定义了特征点对应的极线,从而限制了特征匹配的位置。 相对位姿初步估计:提供相机之间相对位姿的初步估计,但不如Essential矩阵精确。 ### 比较和总结 * Homography矩阵:适用于平面场景和特定的运动情况,可以用于图像配准和特征匹配,但不适用于一般的三维场景。 * Essential矩阵:精确的相机位姿估计和三维重建,需要相机内参。 * Fundamental矩阵:不需要相机内参,可用于特征点匹配的几何约束和初步的相机位姿估计,。 ## 在orb-slam3中,何时会计算这些矩阵,如何根据地图点跟踪相机位姿? 在ORB-SLAM3中,确实在初始化和创建地图点时需要计算Homography矩阵、Essential矩阵或Fundamental矩阵。在系统运行的其他阶段,如相机位姿跟踪和地图点跟踪时,通常不再需要频繁地重新计算这些矩阵,而是依赖于已有的地图点和特征匹配、PnP算法和优化技术实现高效的相机位姿跟踪和地图点的更新。 * 在初始化阶段,计算Essential矩阵、Homography矩阵或Fundamental矩阵来初始化相机位姿和地图点。 * 运动跟踪阶段:通过特征点匹配和PnP算法估计相机位姿,利用局部BA优化相机位姿和地图点位置。 * 跟踪地图点:通过与当前地图中的3D点进行特征匹配,并结合相机位姿预测和优化方法。 然而,计算Homography矩阵、Essential矩阵和Fundamental矩阵不仅仅是在初始化阶段需要,还在以下多个场合中被广泛使用,例如三角化创建地图点、地图点合并、特征匹配等。以下是这些矩阵在具体过程中的应用: ### 三角化创建地图点 计算Essential矩阵和Fundamental矩阵 三角化过程:当ORB-SLAM3在关键帧之间创建新的地图点时,通常需要通过特征匹配确定图像中的对应点,并利用Essential矩阵或Fundamental矩阵计算视图之间的几何关系。通过这些矩阵,可以确定相机间的相对姿态,然后使用三角化方法从不同视角的对应点计算3D点的位置。 ### 地图点合并 计算Homography矩阵 平面检测和合并:在检测到地图中的某些区域为平面时,可以计算Homography矩阵来描述图像之间的平面变换关系。通过Homography矩阵,可以将多个视角下的特征点合并为同一平面上的点,提高地图的精度和一致性。 ### 特征匹配 计算Fundamental矩阵和极线约束 特征点匹配:在特征点匹配过程中,Fundamental矩阵用来约束特征匹配对的位置。通过极线约束,可以显著减少匹配错误,提高匹配的准确性。 极线约束:利用Fundamental矩阵,可以将图像中一个特征点的匹配对限制在另一幅图像的对应极线上,从而减少匹配的计算量和错误率。 ### 其他应用 局部BA和全局BA 局部和全局优化:在局部BA和全局BA(Bundle Adjustment)过程中,Essential矩阵和Fundamental矩阵帮助建立约束关系,通过优化相机位姿和地图点位置,最小化重投影误差,提升整体地图的精度。 ### 总结 用SLAM十四讲的说法, * 2D-2D ( F 1 , F 2 ) (F_1,F_2) (F1,F2) **三角化Triangularization**,特征点匹配,创建地图点 * 2D-2D ( F 1 , F 2 ) (F_1,F_2) (F1,F2) **对极几何**,特征点匹配,减少误匹配并初步估计相机位姿 * 3D-2D ( K F 1 , (KF_1, (KF1, F 1 ) F_1) F1) 地图点和特征点的约束,**PnP**求解相机位姿 * 3D-3D ( K F 1 , K F 2 ) (KF_1,KF_2) (KF1,KF2) 地图点之间,**ICP**匹配,用于地图维护:局部地图融合,精确对齐。 ### ref * [【SLAM模块】多视图几何 - 运动估计_动态slam 多视图几何-CSDN博客](https://blog.csdn.net/dulu_301/article/details/122972428) * [Introduction to Computer Vision (udacity.com)](https://learn.udacity.com/courses/ud810)