原题链接🔗:矩阵置零
难度:中等⭐️⭐️
题目
给定一个 m x n 的矩阵,如果一个元素为 0 ,则将其所在行和列的所有元素都设为 0 。请使用 原地 算法。
示例 1 :
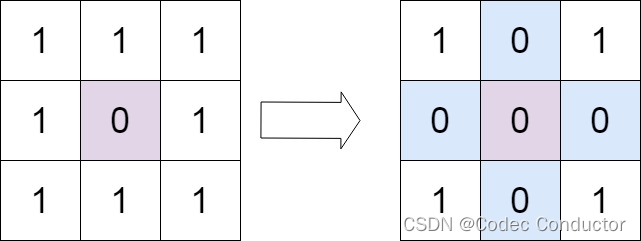
输入:matrix = [[1,1,1],[1,0,1],[1,1,1]]
输出:[[1,0,1],[0,0,0],[1,0,1]]
示例 2 :
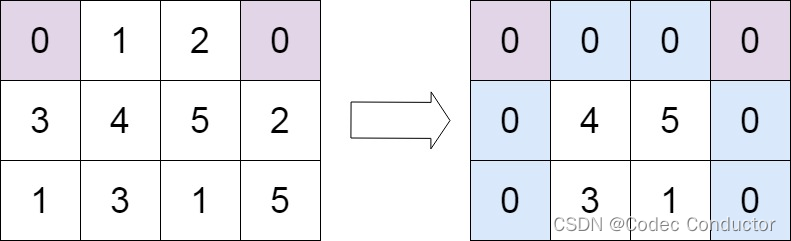
输入:matrix = [[0,1,2,0],[3,4,5,2],[1,3,1,5]]
输出:[[0,0,0,0],[0,4,5,0],[0,3,1,0]]
提示 :
m == matrix.length
n == matrix[0].length
1 <= m, n <= 200
-231 <= matrix[i][j] <= 231 - 1
进阶 :
一个直观的解决方案是使用 O(mn) 的额外空间,但这并不是一个好的解决方案。
一个简单的改进方案是使用 O(m + n) 的额外空间,但这仍然不是最好的解决方案。
你能想出一个仅使用常量空间的解决方案吗?
题解
双标记变量法
- 题解:
LeetCode上的"矩阵置零"问题是一个经典的编程问题,它要求我们修改给定的矩阵,使得所有值为0的元素所在的行和列的所有元素都变为0。以下是解决这个问题的一般思路:
理解问题:首先,我们需要清楚地理解问题的要求,即找到所有值为0的元素,并将它们所在的行和列的所有元素都设置为0。
使用额外空间作为标记:由于我们不能直接在遍历过程中修改矩阵,因为这会干扰我们查找其他0值的位置,我们可以使用额外的空间来标记哪些行和列需要被置零。
遍历矩阵:首先,我们遍历矩阵,找到所有的0值,并记录下这些0值所在的行和列。
标记行和列:在第一次遍历中,我们可以使用两个布尔变量来标记第一行和第一列是否需要被置零。如果第一行或第一列中有0,则在后续的遍历中,我们可以使用第一行和第一列作为标记。
使用第一行和第一列作为辅助空间:在第二次遍历中,我们将第一行和第一列作为辅助空间来标记其他行和列的置零状态。如果一个元素是0,我们就在对应的行的第一个元素和列的第一个元素上标记0。
根据标记修改矩阵:在第二次遍历结束后,我们根据第一行和第一列的标记来修改矩阵中的其他元素。如果第一行或第一列的某个元素是0,则我们知道整行或整列都需要被置零。
处理第一行和第一列:最后,我们需要单独处理第一行和第一列,因为它们被用作了标记空间,不能在之前的步骤中被修改。
优化空间复杂度:上述方法使用了额外的标记空间,但实际上,我们可以通过一些技巧来避免使用这些额外的空间,例如使用矩阵的第一个元素来标记第一行和第一列的状态。
编写代码:根据上述思路,编写代码实现算法。
测试:编写测试用例来验证你的算法是否正确处理了各种情况,包括但不限于空矩阵、矩阵中没有0、矩阵中只有0等。
这个算法的时间复杂度是O(m*n),其中m和n分别是矩阵的行数和列数。空间复杂度可以优化到O(1),如果我们不使用额外的布尔变量来单独标记第一行和第一列,而是使用矩阵的第一个元素来存储这两个状态。
- 复杂度:时间复杂度是O(m*n),空间复杂度是O(1)。
- 过程:
类定义:Solution 类定义了一个公共成员函数 setZeroes,用于处理矩阵。
函数参数:setZeroes 函数接收一个二维 vector 类型的参数 matrix。
矩阵大小获取:首先获取矩阵的行数 m 和列数 n。
标记行和列:使用两个布尔变量 firstRowHasZero 和 firstColHasZero 来标记第一行和第一列是否需要置零。
遍历矩阵:首先遍历第一行和第一列,检查是否有0,如果有,则设置相应的标记变量。
使用标记进行标记:然后遍历矩阵的其余部分,使用第一行和第一列作为标记,将对应的行和列标记为0。
置零操作:根据标记,将矩阵中标记为0的行和列置零。
特殊情况处理:最后,如果第一行或第一列需要置零,使用 fill 函数或循环将它们置零。
测试代码:在 main 函数中创建了一个示例矩阵,并调用 setZeroes 函数来修改它。然后输出修改后的矩阵。
- c++ demo:
cpp
#include <vector>
#include <algorithm> // 用于std::fill函数
#include <iostream>
using namespace std;
class Solution {
public:
void setZeroes(vector<vector<int>>& matrix) {
int m = matrix.size();
if (m == 0) return;
int n = matrix[0].size();
// 使用两个变量来记录第一行和第一列是否需要置零
bool firstRowHasZero = false, firstColHasZero = false;
// 遍历矩阵,找出第一行和第一列的0
for (int i = 0; i < m; i++) {
if (matrix[i][0] == 0) {
firstColHasZero = true;
break;
}
}
for (int j = 0; j < n; j++) {
if (matrix[0][j] == 0) {
firstRowHasZero = true;
break;
}
}
// 使用第一行和第一列作为标记,遍历矩阵
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
if (matrix[i][j] == 0) {
matrix[0][j] = 0;
matrix[i][0] = 0;
}
}
}
// 根据第一行和第一列的标记,将对应的行和列置零
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
if (matrix[i][0] == 0 || matrix[0][j] == 0) {
matrix[i][j] = 0;
}
}
}
// 如果第一行需要置零,则置零
if (firstRowHasZero) {
fill(matrix[0].begin(), matrix[0].end(), 0);
}
// 如果第一列需要置零,则置零
if (firstColHasZero) {
for (int i = 0; i < m; i++) {
matrix[i][0] = 0;
}
}
}
};
// 测试代码
int main() {
vector<vector<int>> matrix = {
{1, 1, 1},
{1, 0, 1},
{1, 1, 1}
};
Solution solution;
solution.setZeroes(matrix);
// 输出结果
for (const auto& row : matrix) {
for (int val : row) {
cout << val << " ";
}
cout << endl;
}
return 0;
}- 输出结果:
1 0 1
0 0 0
1 0 1
