来自JMLR的一篇论文,https://www.jmlr.org/papers/volume24/21-1441/21-1441.pdf
这篇文章试图通过分析模型权重矩阵的频谱来解释模型,并在此基础上提出了一种用于早停的频谱标准。
1,分类难度对权重矩阵谱的影响
1.1 相关研究
在最近针对深度模型的可解释性研究中,出现了一种流行的方法,即对DNNs的各种大型特征随机矩阵进行谱分析,所谓大型特征随机矩阵,就是例如反向传播算法的Hessian矩阵、不同层之间的权重矩阵以及输出特征的协方差矩阵等。这样的谱分析有助于深入了解DNNs的行为。
1.2 权重矩阵的谱的类型
权重矩阵的谱在训练的最后阶段被分类为三种类型:轻尾(LT)、块过渡期(BT)和重尾(HT)。
重尾(Heavy Tails)、轻尾(Light Tails)和块过渡(Bulk Transition)是指权重矩阵或Hessian矩阵的特征值分布的不同类型。区别如下:
1)重尾分布指的是在特征值分布的尾部存在较大概率密度,即存在一些非常大的特征值。在深度学习中,重尾可能表明权重矩阵中存在高度相关的条目,这可能导致过拟合或模型的泛化能力下降。
2)轻尾分布的特征是特征值分布的尾部概率密度较低,即特征值普遍较小,没有特别大的异常值。在深度学习中,轻尾可能表示权重矩阵的正则化较好,有助于提高模型的泛化能力。
3)块过渡是一种介于重尾和轻尾之间的状态,特征值分布的主体(块)接近Marcenko-Pastur分布,但可能存在一些异常的"尖峰"或"离群点"。这种状态可能表明模型正在从过拟合状态(重尾)过渡到更好的泛化状态(轻尾),或者是模型训练过程中的一个中间阶段。
1.3 如何计算权重矩阵的谱
对权重矩阵计算其Gram矩阵,接着求解Gram矩阵的特征值。接着将计算出的特征值按降序排列,以便于分析最大的特征值。最后,构建经验谱分布,这是一个经验分布函数,用于估计权重矩阵特征值的分布。ESD可以通过直方图或核密度估计来实现。
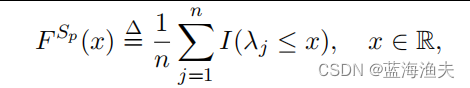
其中I是指示函数,当括号内的表达式为真时,I的值为1;否则为0。
1.4作者的发现
作者发现分类难度是影响权重矩阵谱中出现HT的一个重要因素。分类难度越高,HT出现的几率越大。在合成数据集和真实数据集上进行的实验都支持这一发现。特别是,降低数据集的信噪比或在高斯数据实验中增加类别数量K,都会增加分类难度,并在训练结束时产生重尾。在真实数据实验中,由于CIFAR10具有更复杂的特征和更高的分类难度,因此在CIFAR10的实验中出现重尾的情况比在MNIST的实验中更多。
2,基于权重矩阵谱的早停准则
2.1 内容
本文提出的基于谱的早停策略通过分析深度神经网络(DNN)权重矩阵的谱特性来确定训练过程中的停止时机。
步骤:
1)权重矩阵的谱分析:这涉及到计算权重矩阵的非零特征值.
2)特征值排序与检测:将这些特征值按降序排列,并使用算法自动检测特征值中的"尖峰"(spikes),即那些远离其他特征值的特征值。
3)计算谱准则值 :**也就是计算权重矩阵的谱与Marcenko-Pastur (MP) 定律的偏差。**这涉及到构造一个直方图估计器来近似权重矩阵特征值的联合密度,并与MP定律的密度函数进行比较。
距离的定义是这样的
其中是ESD的直方图估计,公式如下

其中, ,对于一个n×p的随机矩阵,其中n/p→c(c是一个正常数)。
,对于一个n×p的随机矩阵,其中n/p→c(c是一个正常数)。是权重矩阵元素的方差。参数 M 通常表示直方图估计中使用的"bins"或"binsize"的数量,用于将数据分成多个区间以估计概率密度函数,本文设置为
。B(x) 表示的是一个函数,它将一个实数 x 映射到包含 x 的"bin"或区间。在频谱分析中,B(x)可以用于计算每个区间内的点的数量,从而估计概率密度函数或特征值分布。
而后一项是MP分布的密度函数,公式如下:
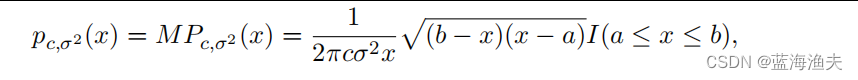
MP分布可用于描述大随机矩阵特征值的分布。MP定律与DNN的泛化能力有关。接近MP分布的谱可能意味着模型具有较好的泛化能力,而偏离MP分布可能指示过拟合或其他问题。
4)设定阈值:该值基于L1距离
5)监控训练过程:在训练过程中,对于每个训练周期,计算权重矩阵的谱准则值
6)判断停止时机:如果在连续的几个训练周期中,谱准则值超过了阈值,则认为达到早停条件。
2.2 相较于传统早停策略的优势
1)不需要测试集:传统早停依赖于对模型在测试集上的准确率或者loss的测量,而本文提出的基于谱分析的早停策略完全不需要测试集。只要分析训练集上的权重矩阵的谱就可以了
2)适应性强:因为是依靠权重矩阵的谱分析而不是测试集,所以数据类型或者数据集组成结构等影响较小
3)鲁棒性更强:实验证明,即使训练准确率还在上升,本方法依然能实现早停。