二叉树从入门到AC（3）完全二叉树与堆

完全二叉树与堆

前言

本文算是补充之前的系列，在前文中，讲了二叉树的基本结构与应用
二叉树从入门到AC（1）构建和前中后序遍历
 二叉树从入门到AC（2）深度与层次遍历
二叉树的特殊形态

二叉树有两种常用的特殊形态：满二叉树和完全二叉树。如果一颗二叉树，其内部每个结点都有左右儿子 ，我们称之为满二叉树，这很好理解，如图所示：

我们在满二叉树中的最后一层，从右往左连续拔去至少零个结点 ，便是完全二叉树。也就是说，满二叉树是一种特殊的完全二叉树 。

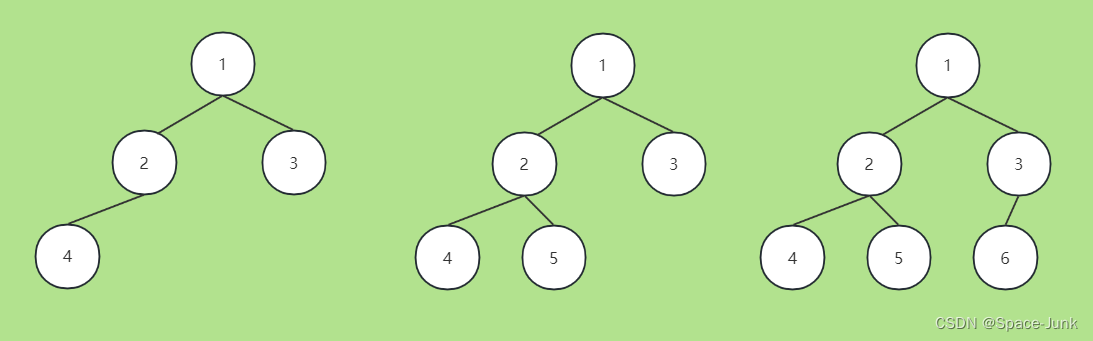
以上都为完全二叉树

那么如何判断一棵树是不是完全二叉树呢？我们可以运用层次遍历的结构（前文有代码），首先将储存一颗非空树，在队列中遵循：

1.如果遇到一个结点，左孩子为空，右孩子不为空，则该树一定不是完全二叉树

2.如果遇到一个结点，左孩子不为空，右孩子为空；或者左右孩子都为空，且则该节点之后的队列中的结点都为叶子节点，该树才是完全二叉树

3.以上两个一直都没触发，说明是满二叉树

优先队列：堆

堆，是一种特殊的完全二叉树，每个结点储存一个值，其中，若所有父结点都小于其子结点，称为最小堆，反之则是最大堆。如图：

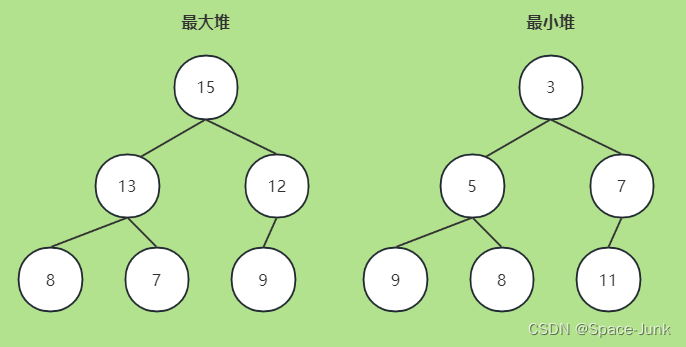
二叉堆是一种基础数据结构，C++ 的STL中的优先队列就是使用二叉堆。另外，堆排序也是一种二叉堆算法。

堆的作用主要面向一个问题：如何高效的在一组数据中任意插入删除任何值的情况下，始终找到最小值/最大值。

这种数据结构也被称为优先队列。

向下调整维护堆

以上图的最小堆为例，在数组中按层次遍历储存为3，5，7，9，8，11

要求：不限次数的删除最小值并插入进新的值，保持堆的属性（最小值在堆顶）

这时候我们删除堆顶的最小值3，并且添加任意一个数如10到堆顶，只要能维护这个堆的属性，我们就可以得到新的最小值。

于是设计算法，我们从堆顶开始 反复执行：把当前结点与左右儿子比对，并与最小的那个结点交换值，直到无法交换 （要么是左右儿子都更大，要么是到叶子结点了）

如图所示：

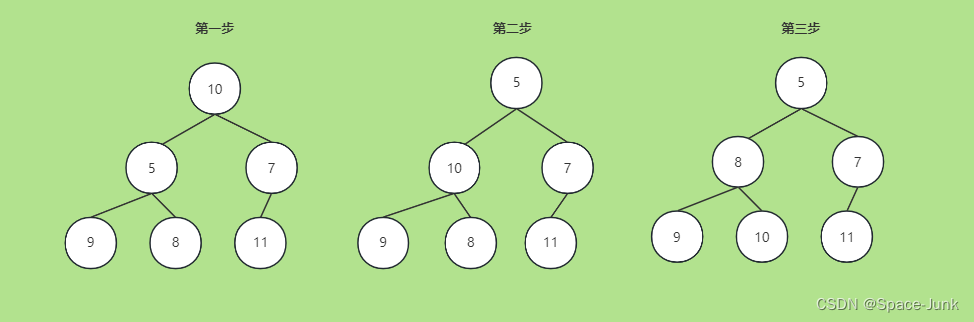
于是我们维护住了一个最小堆，最大堆也是同理。那么在代码层就好写多了，我们可以根据数组下标发现，设当前结点下标为i,我们只需要每次与2i和2 i+1相比并判断是否Swap就好

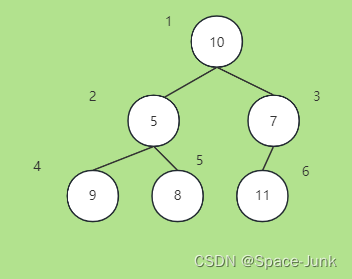
c 复制代码

void Sswap(int a,int b)
{
    int c=0;
    c=arr[b];
    arr[b]=arr[a];
    arr[a]=c;
}
void siftdown(int i)//向下调整，用于寻找最值
{
    int t=0,flag=0;
    while(i*2<=n&&flag==0)
    {
        if(arr[i]>arr[i*2])
        t=i*2;
        else
            t=i;
        if(t*2+1<=n)
        {
            if(arr[t]>arr[i*2+1])
                t=i*2+1;
        }
        if(t!=i)
        {
            Sswap(t,i);//交换两结点的值
            i=t;
        }
        else
            flag=1;
    }
}

在主函数中，我们将数组调整为全局变量，并且i始终设为0，例如

c 复制代码

int arr[6]={10,5,7,9,8,11};
int n=5;
int main()
{
    siftdown(0);
    for(int i=0;i<=n;i++)
    {
        printf("%d ",arr[i]);
    }
    return 0;
}

执行结果：

向上调整维护堆

如果我们需要不断向堆中添加数值而不删除数值怎么办？那么我们可以从下面的叶子结点开始添加，并逐一往上比对，来维护堆。

c 复制代码

void siftup(int i)
{
    int flag=0;
    if(i==0)
        return;
    while(i!=0&&flag==0)
    {
        if(arr[i]<arr[i/2])
            Sswap(i,i/2);
        else
            flag=1;
        i=i/2;
    }
}

我们将：arr[6]={3,5,7,9,8,1};

与i=5代入，

这便是堆的维护操作。

堆的作用

当我们输入一个数组，并求其最值时，我们一般会开max或min比对每个数并保留最值，这是时间复杂度最低的做法，为O(N)。但是当我们删除最小值并添加进一个新值之后，就相当于需要彻底进行一次重新排序，复杂度也来到了O(N^2)，而同样的目的，由于堆的特性，维护起来只需要logN的时间。

那么我们如何用完全无序的数列建立一个堆呢？

c 复制代码

void creat()
{
    int i=0;
    for(i=n/2;i>=0;i--)
    {
        siftdown(i);
    }
}

即可。

在创建了堆之后，我们还有著名的排序方法，堆排序，网上到处都有模板在这里不赘述。另外，堆也是一种重要的优化思路出现在别的算法中，主旨都在于用更短的时间来在插入、删除元素的情况下捕捉最值（或者第n大的值也可以）。