论文阅读ReLU-KAN和Wav-KAN

这是我读KAN系列论文的第三篇，今天把两篇论文放在一起写，分别是：

ReLU-KAN：

https://arxiv.org/abs/2406.02075

Wav-KAN：

https://arxiv.org/abs/2405.12832

之所以放在一起，是因为这两篇论文针对KAN的改进思路是相似的，都是采用新的基函数，来替代KAN中的B样条函数。

（另一个原因是这两篇文章内容都比较少，笑）

1，ReLU-KAN

1.1原理

作者提出了一种新的ReLU激活函数和逐点乘法来简化KAN的基函数设计，从而优化计算过程以实现高效的CUDA计算。通过将整个基函数计算表达为矩阵操作，充分利用了GPU的并行处理能力。此外，运用了类似于Transformer中的定位编码，预生成了非训练参数以加速计算。

作者提出的新基函数如下

作者直接给出了ReLU-KAN的层的pytorch代码

python 复制代码

import numpy as np
import torch
import torch.nn as nn

class ReLUKANLayer(nn.Module):
    def __init__(self, input_size: int, g: int, k: int, output_size: int):
        super().__init__()
        self.g, self.k, self.r = g, k, 4*g*g / ((k+1)*(k+1))
        self.input_size, self.output_size = input_size, output_size
        phase_low = np.arange(-k, g) / g # 计算ReLU函数的下限参数
        phase_height = phase_low + (k+1) / g # 计算ReLU函数的上限参数
        self.phase_low = nn.Parameter(torch.Tensor(np.array([phase_low for i in range(input_size)])), requires_grad=False) # 将phase_low作为不可训练的参数
        self.phase_height = nn.Parameter(torch.Tensor(np.array([phase_height for i in range(input_size)])),requires_grad=False) # 将phase_height作为不可训练的参数
        self.equal_size_conv = nn.Conv2d(1, output_size, (g+k, input_size))

    def forward(self, x):
        x1 = torch.relu(x - self.phase_low) # 第一个ReLU激活，减去phase_low
        x2 = torch.relu(self.phase_height - x) # 第二个ReLU激活，x减去phase_height
        x = x1 * x2 * self.r # ReLU激活结果的逐点乘积，乘以归一化常数r
        x = x * x 
        x = x.reshape((len(x), 1, self.g + self.k, self.input_size))
        x = self.equal_size_conv(x)
        x = x.reshape((len(x), self.output_size, 1))
        return x

1.2实验结果

从实验结果看，训练速度确实得到了极大的提升。

2，Wav-KAN

2.1原理

作者用小波函数替换了B样条，从而提高准确性、加快训练速度，并增加鲁棒性。此外，小波函数能够提供多分辨率分析，有效捕捉数据的高频和低频特征。

2.2实验结果

在MNIST上的实验结果：

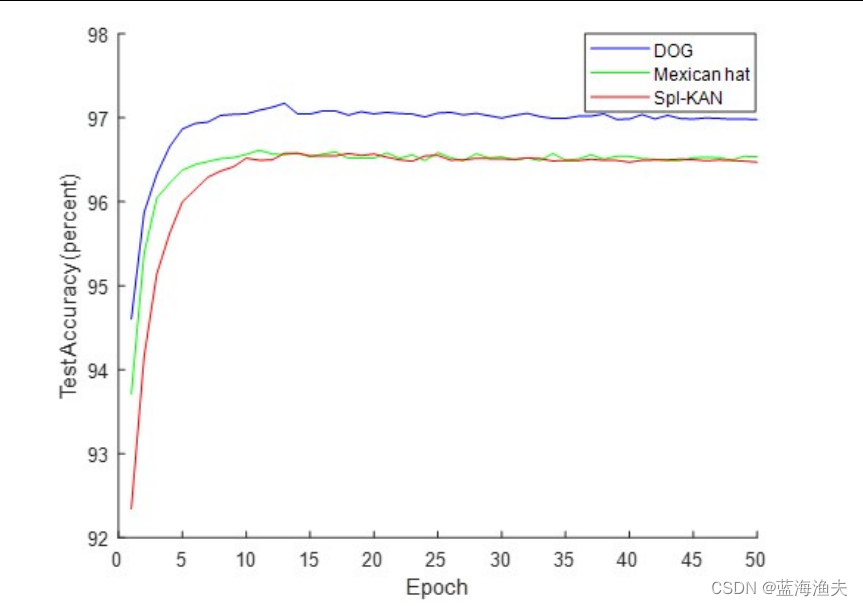
其中Mexican hat和Derivative of Gaussian (DOG)对应的是不同类型的母小波函数。spl-KAN指的就是用B样条的原始KAN