目录
[羊皮效应和模糊 RDD(Fuzzy RDD)](#羊皮效应和模糊 RDD(Fuzzy RDD))
[麦克雷测试(McCrary Test)](#麦克雷测试(McCrary Test))
羊皮效应和模糊 RDD(Fuzzy RDD)
关于教育对收入的影响,经济学有两种主要观点。第一个是广为人知的论点,即教育增加了人力资本,提高了生产力,从而提高了收入。从这个观点来看,教育实际上会让你变得更好。另一种观点认为,教育只是一种信号机制。它只是让您完成所有这些艰巨的测试和学术任务。如果你能做到,它就向市场表明你是一名优秀的员工。这样,教育不会让你更有效率。它只会告诉市场你一直以来的生产力。这里重要的是文凭。如果你有它,你会得到更多的报酬。我们将此称为羊皮效应,因为过去文凭是用羊皮印刷的。
为了检验这一假设,Clark and Martorell 使用断点回归来衡量 12 年级毕业对收入的影响。为了做到这一点,他们必须考虑一些运行变量,使高于它的学生毕业,而低于它的学生则不毕业。他们在德克萨斯州的教育系统中发现了这样的数据。
为了在德克萨斯州毕业,必须通过考试。考试从 10 年级开始,学生可以做多次,但最终,他们将在 12 年级末面临最后一次考试机会。这个想法是从参加最后一次考试机会的学生那里获取数据,并将那些几乎没有通过考试的学生与那些勉强通过考试的学生进行比较。这些学生将拥有非常相似的人力资本,但不同的资质水平。也就是说,那些勉强通过的人也将获得文凭。
python
sheepskin = pd.read_csv("./data/sheepskin.csv")[["avgearnings", "minscore", "receivehsd", "n"]]
sheepskin.head()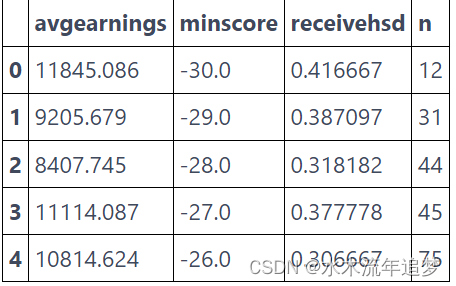
再次,此数据按运行变量分组。 它不仅包含运行变量(minscore,已经以零为中心)和结果(avgearnings),而且还包含在该分数单元中接收文凭的概率和调用的大小 (n)。 因此,例如,在分数低于阈值 -30 的单元格中的 12 名学生中,只有 5 人能够获得文凭 (12 * 0.416)。
这意味着干预分配中存在一些滑移。 一些低于及格门槛的学生无论如何都设法获得了文凭。 在这里,回归的断点是模糊的,而不是干脆清晰的。 请注意获得文凭的概率不会在阈值处从零跳到一。 但它确实从 50% 跃升至 90%。
python
sheepskin.plot.scatter(x="minscore", y="receivehsd", figsize=(10,5))
plt.xlabel("Test Scores Relative to Cut off")
plt.ylabel("Fraction Receiving Diplomas")
plt.title("Last-chance Exams");
我们可以将模糊 RD 视为一种不合规性。通过门槛应该让每个人都能获得文凭,但是那些"从不接受"的学生,却没有得到它。同样,低于门槛应该会阻止你获得文凭,但是那些"总是接受"的学生,无论如何都设法获得它。
就像当我们有潜在的结果时,我们在这种情况下也有潜在的干预状态。 T1是每个人在超过阈值时都会得到的待遇。 T0 是每个人在低于阈值时都会得到的待遇。您可能已经注意到,我们可以将阈值视为工具变量 。就像在 IV 中一样,如果我们直接地估计干预效果,它将偏向零值。
干预的概率小于 1,甚至高于阈值,使得我们观察到的结果小于真正的潜在结果 Y1。出于同样的原因,我们观察到的低于阈值的结果高于真正的潜在结果 Y0。这使得阈值处的干预效果看起来比实际要小,我们将不得不使用 IV 技术来纠正它。
就像我们假设潜在结果的平稳性一样,我们现在假设它用于潜在的治疗。此外,我们需要假设单调性,就像在 IV 中一样。万一你不记得了,它说明了 。这意味着从左到右越过门槛只会增加您获得文凭的机会(或者没有拒绝者)。有了这两个假设,我们就有了 LATE 的 Wald Estimator。
请注意,这是在两种意义上的局部估计。首先,它之所以是局部的,因为它只给出阈值 c 处的处理效果。这是 RD 位置。其次,它之所以是局部的第二个原因,在于它只估计服从者的处理效果。这是 IV 位置。
为了估计这一点,我们将使用 2 线性回归。可以像我们之前所做的那样估计分子。为了得到分母,我们只需将结果替换为处理。但首先,让我们谈谈我们需要运行的健全性检查,以确保我们可以信任我们的 RDD 估计。
麦克雷测试(McCrary Test)
可能打破我们 RDD 论点的一件事是,人们是否可以操纵他们站在门槛的位置。在羊皮示例中,如果刚好低于阈值的学生找到一种绕过系统的方法来稍微提高他们的考试成绩,就会发生这种情况。另一个例子是当您需要低于某个收入水平才能获得政府福利时。一些家庭可能会故意降低收入,只是为了有资格参加该计划。
在这种情况下,我们往往会看到一种现象,即运行变量密度上的聚束现象(bunching)。这意味着我们将有很多实体略高于或略低于阈值。为了检查这一点,我们可以绘制运行变量的密度函数并查看阈值周围是否有任何尖峰。对于我们的例子,密度由我们数据中的"n"列给出。
python
plt.figure(figsize=(8,8))
ax = plt.subplot(2,1,1)
sheepskin.plot.bar(x="minscore", y="n", ax=ax)
plt.title("McCrary Test")
plt.ylabel("Smoothness at the Threshold")
ax = plt.subplot(2,1,2, sharex=ax)
sheepskin.replace({1877:1977, 1874:2277}).plot.bar(x="minscore", y="n", ax=ax)
plt.xlabel("Test Scores Relative to Cut off")
plt.ylabel("Spike at the Threshold");
第一个图显示了我们的数据密度如何。 正如我们所见,阈值周围没有尖峰,这意味着没有聚束。 学生们并没有操纵他们可以落在门槛上的哪个地方。 这里仅出于说明目的,第二个图显示了如果学生可以操纵他们落在阈值的位置,那么聚束会是什么样子。 我们会看到刚刚超过阈值的单元格的密度出现峰值,因为许多学生会在那个单元格上,勉强通过考试。
解决这个问题,我们可以回过头来估计羊皮效应。 正如我之前所说,Wald 估计器的分子可以像我们在 Sharp RD 中一样进行估计。 在这里,我们将使用带宽为 15 的核函数作为权重。由于我们还有单元格大小,我们将核函数乘以样本大小以获得单元格的最终权重。
python
sheepsking_rdd = sheepskin.assign(threshold=(sheepskin["minscore"]>0).astype(int))
model = smf.wls("avgearnings~minscore*threshold",
sheepsking_rdd,
weights=kernel(sheepsking_rdd["minscore"], c=0, h=15)*sheepsking_rdd["n"]).fit()
model.summary().tables[1]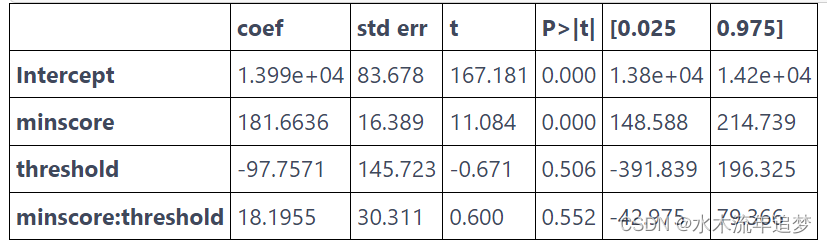
这告诉我们文凭的效果是 -97.7571,但这在统计上并不显着(P 值为 0.5)。 如果我们绘制这些结果,我们会在阈值处得到一条非常连续的线。 受过更多教育的人确实赚了更多的钱,但在他们获得 12 年级文凭的时候并没有飞跃。 这个论据支持这样一种观点,即教育通过提高人们的生产力来增加收入,而不仅仅是通过文凭给出一个信号。 换句话说,没有羊皮效应。
python
ax = sheepskin.plot.scatter(x="minscore", y="avgearnings", color="C0")
sheepskin.assign(predictions=model.fittedvalues).plot(x="minscore", y="predictions", ax=ax, color="C1", figsize=(8,5))
plt.xlabel("Test Scores Relative to Cutoff")
plt.ylabel("Average Earnings")
plt.title("Last-chance Exams");
然而,正如我们从不服从偏差的工作方式中知道的那样,这个结果偏向于零。 为了纠正这个问题,我们需要在第一阶段对其进行缩放并获得 Wald 估计量。 不幸的是,没有一个好的 Python 实现,所以我们必须手动完成并使用自助抽样法来获取标准误。
下面的代码运行 Wald 估计器的分子,就像我们之前所做的一样,还通过将目标变量替换为干预变量"receivehsd"来构造分母。 最后一步只是将分子除以分母。
python
def wald_rdd(data):
weights=kernel(data["minscore"], c=0, h=15)*data["n"]
denominator = smf.wls("receivehsd~minscore*threshold", data, weights=weights).fit()
numerator = smf.wls("avgearnings~minscore*threshold", data, weights=weights).fit()
return numerator.params["threshold"]/denominator.params["threshold"]
from joblib import Parallel, delayed
np.random.seed(45)
bootstrap_sample = 1000
ates = Parallel(n_jobs=4)(delayed(wald_rdd)(sheepsking_rdd.sample(frac=1, replace=True))
for _ in range(bootstrap_sample))
ates = np.array(ates)
## 使用自助法的样本,我们可以画出ATE的分布,并看到95%置信区间在什么地方。
sns.distplot(ates, kde=False)
plt.vlines(np.percentile(ates, 2.5), 0, 100, linestyles="dotted")
plt.vlines(np.percentile(ates, 97.5), 0, 100, linestyles="dotted", label="95% CI")
plt.title("ATE Bootstrap Distribution")
plt.xlim([-10000, 10000])
plt.legend();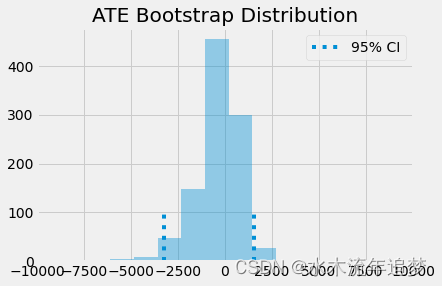
如您所见,即使我们按第一阶段缩放效果,它仍然与零没有统计学差异。这意味着教育不是通过简单的羊皮效应来增加收入,而是通过提高一个人的生产力。
关键思想
我们学会了如何利用人为的不连续性来估计因果效应。这个想法是我们将有一些人为的阈值,使干预的概率跳跃。我们看到的一个例子是年龄如何使饮酒的概率在 21 岁时跃升。我们可以用它来估计饮酒对死亡率的影响。我们利用了在非常接近阈值的地方,我们有一些接近随机试验的东西这样一个事实。非常接近阈值的实体可能会采取任何一种方式,而决定它们落在何处基本上是随机的。有了这个,我们可以比较上面和下面的那些,以获得干预效果。我们看到了如何通过使用核函数的加权线性回归来做到这一点,以及这个方法如何自动地为我们的 ATE 提供标准误估计。
然后,我们看看在模糊 RD 设计中会发生什么,这里存在不服从的样本点。我们看到可以采用对IV的方式一样来处理这种情况。