回归预测 | Matlab实现GWO-ESN基于灰狼算法优化回声状态网络的多输入单输出回归预测
目录
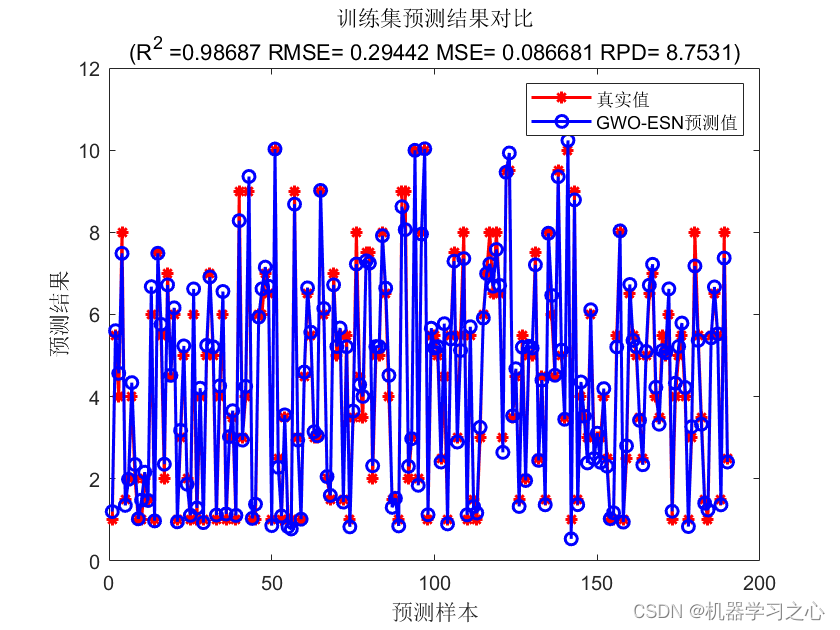
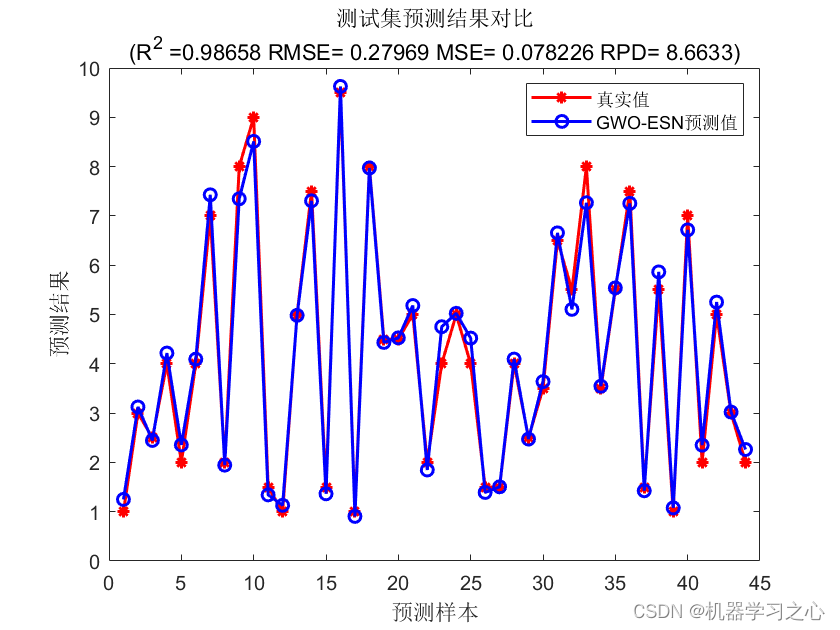
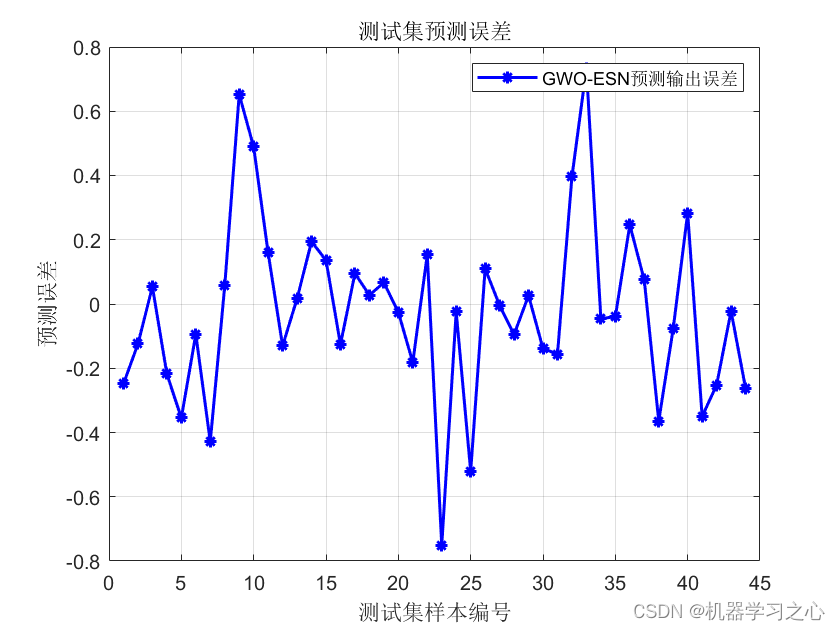
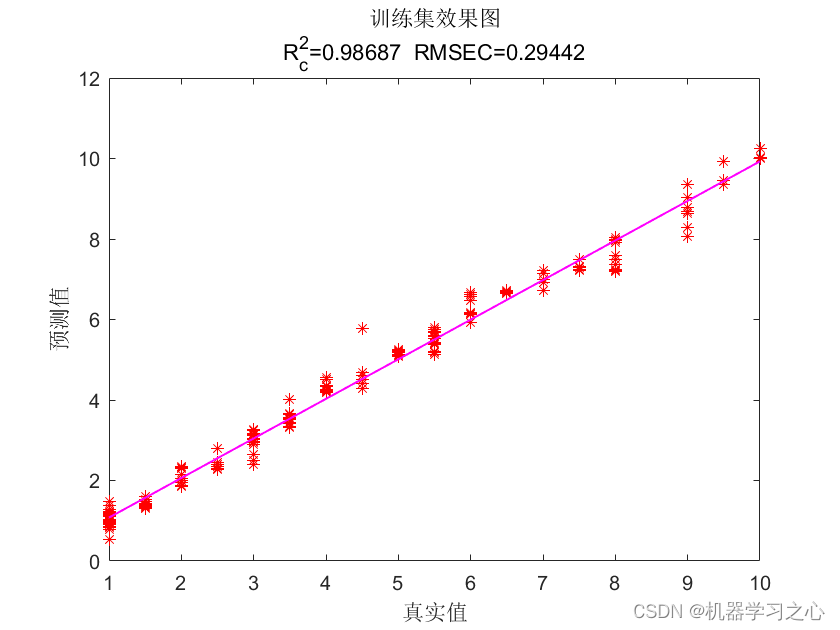
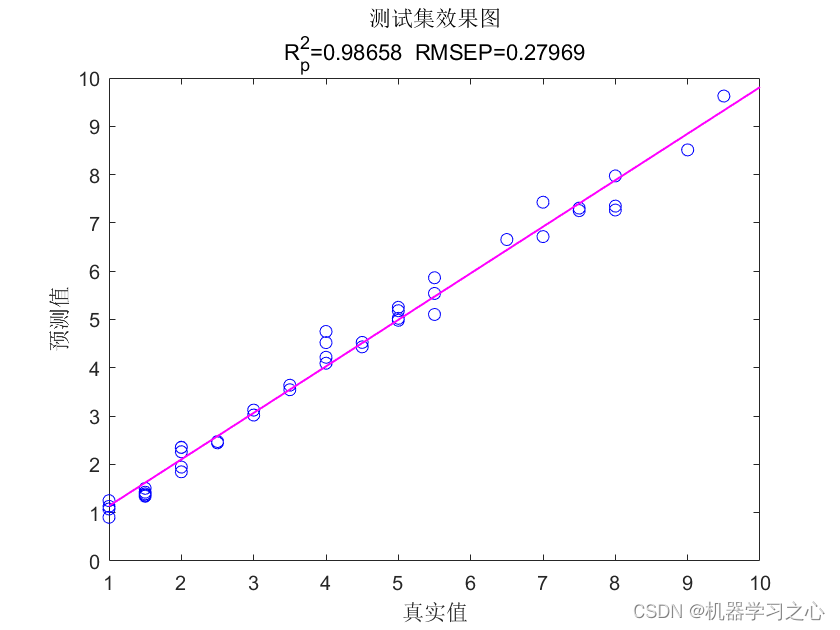
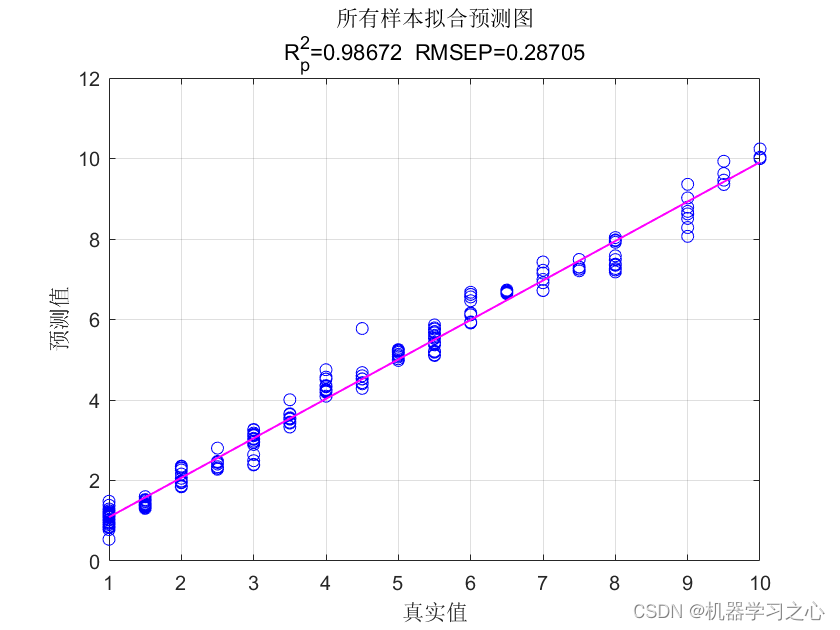
预测效果
基本介绍
1.Matlab实现GWO-ESN基于灰狼算法优化回声状态网络的多输入单输出回归预测(完整源码和数据);
2.数据集为excel,多输入单输出数据集,运行主程序main.m即可,其余为函数文件,无需运行;
3.优化的参数为:三个参数,储备池规模,学习率,正则化系数。命令窗口输出RMSE、MAPE、MAE、R2等评价指标;
4.运行环境Matlab2018b及以上;
5.代码特点:参数化编程、参数可方便更改、代码编程思路清晰、注释明细。
程序设计
- 完整源码和数据获取方式资源处直接下载Matlab实现GWO-ESN基于灰狼算法优化回声状态网络的多输入单输出回归预测。
clike
%% 清空环境变量
warning off % 关闭报警信息
close all % 关闭开启的图窗
clear % 清空变量
clc % 清空命令行
%% 数据归一化
[p_train, ps_input] = mapminmax(P_train, 0, 1);
p_test = mapminmax('apply', P_test, ps_input);
[t_train, ps_output] = mapminmax(T_train, 0, 1);
t_test = mapminmax('apply', T_test, ps_output);
%% 参数设置
fun = @getObjValue; % 目标函数
dim = 3; % 优化参数个数
lb = [100, 0.001, 0.001]; % 优化参数目标下限(储备池规模,学习率,正则化系数)
ub = [800, 2.000, 0.100]; % 优化参数目标上限(储备池规模,学习率,正则化系数)
pop = 10; % 数量
Max_iteration = 20; % 最大迭代次数
Init = 30; % 初始化储备池(样本数)
%% 优化算法
[Best_score,Best_pos, curve] = GWO(pop, Max_iteration, lb, ub, dim, fun);
%% 获取最优参数
hidden = round(Best_pos(1)); % 储备池规模
lr = Best_pos(2); % 学习率(更新速度)
reg = Best_pos(3); % 正则化系数
%% 训练模型
net = esn_train(p_train, t_train, hidden, lr, Init, reg);
%% 预测
t_sim1 = esn_sim(net, p_train);
t_sim2 = esn_sim(net, p_test );
%% 数据反归一化
T_sim1 = mapminmax('reverse', t_sim1, ps_output);
T_sim2 = mapminmax('reverse', t_sim2, ps_output);
%% 均方根误差
error1 = sqrt(sum((T_sim1 - T_train).^2) ./ M);
error2 = sqrt(sum((T_sim2 - T_test ).^2) ./ N);
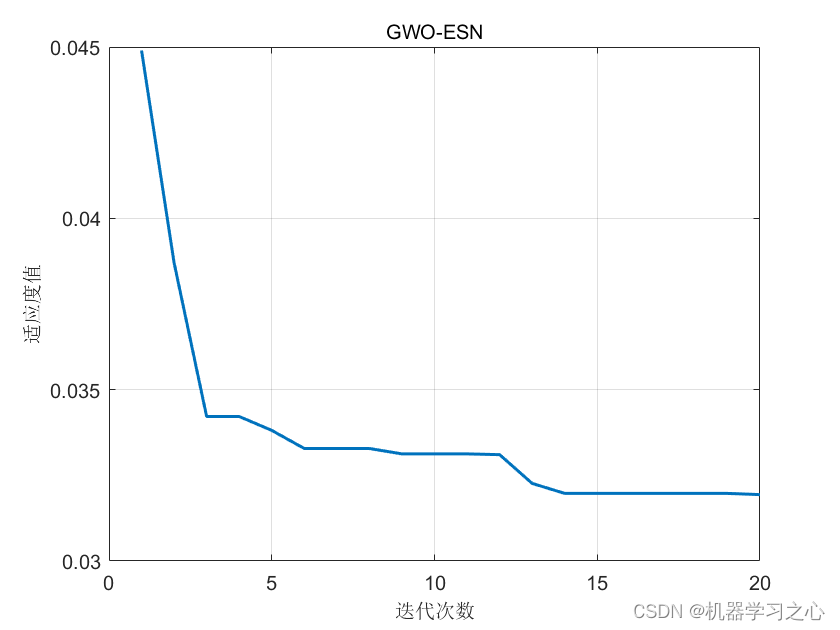
%% 适应度曲线
figure
plot(1 : length(curve), curve, 'LineWidth', 1.5);
title('SSA-ESN', 'FontSize', 10);
xlabel('迭代次数', 'FontSize', 10);
ylabel('适应度值', 'FontSize', 10);
grid on
%% 绘图
%% 测试集结果
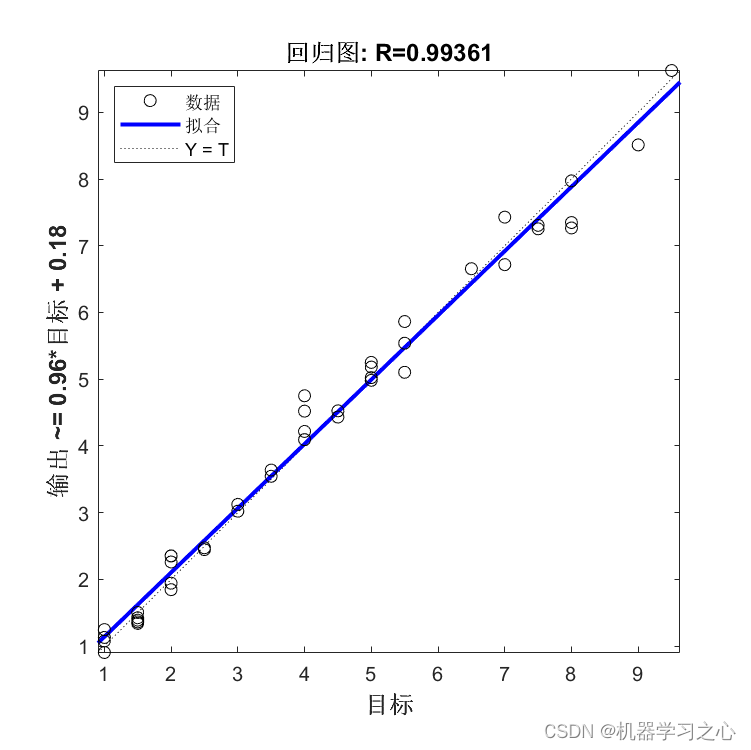
figure;
plotregression(T_test,T_sim2,['回归图']);
figure;
ploterrhist(T_test-T_sim2,['误差直方图']);
%% 均方根误差 RMSE
error1 = sqrt(sum((T_sim1 - T_train).^2)./M);
error2 = sqrt(sum((T_test - T_sim2).^2)./N);
%%
%决定系数
R1 = 1 - norm(T_train - T_sim1)^2 / norm(T_train - mean(T_train))^2;
R2 = 1 - norm(T_test - T_sim2)^2 / norm(T_test - mean(T_test ))^2;
%%
%均方误差 MSE
mse1 = sum((T_sim1 - T_train).^2)./M;
mse2 = sum((T_sim2 - T_test).^2)./N;
% CSDN 机器学习之心参考资料
1\] https://blog.csdn.net/kjm13182345320/article/details/128577926?spm=1001.2014.3001.5501 \[2\] https://blog.csdn.net/kjm13182345320/article/details/128573597?spm=1001.2014.3001.5501