高等数学公式汇总
一、三角函数公式
1、特殊值
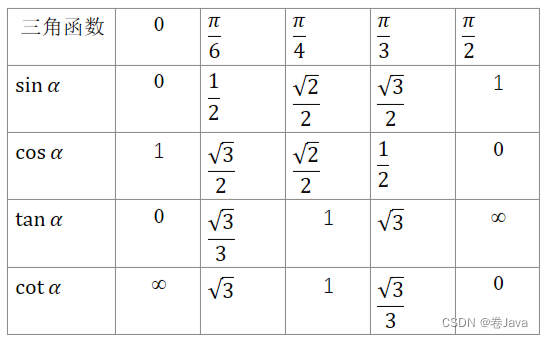
2、二倍角和差公式
1)正余弦和差公式
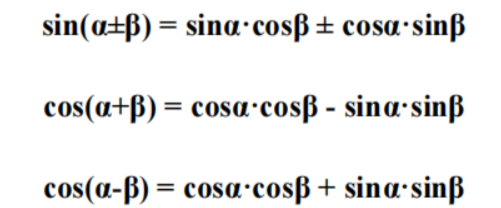
2)正切和差公式
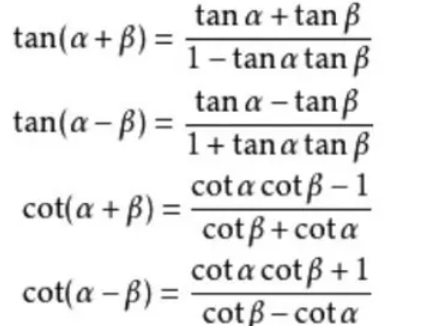
3)积化和差
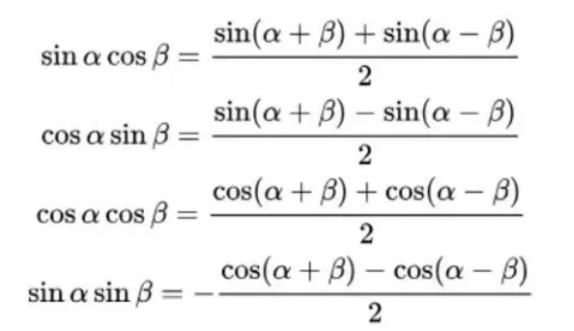
4)和差化积

3、平方和公式
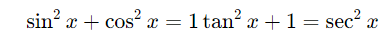
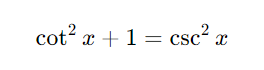
4、倍角公式
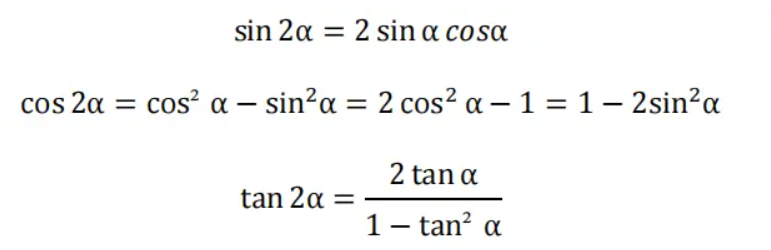
5、半角公式
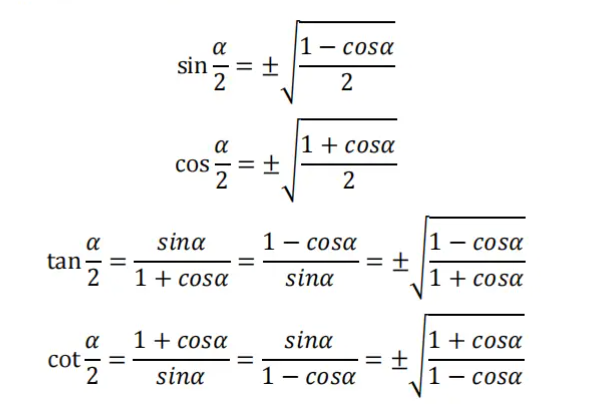
6、万能公式

7、辅助角公式
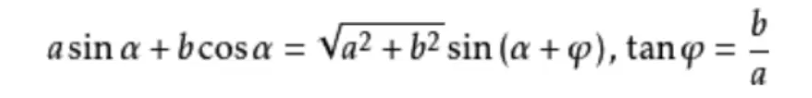
二、反三角函数公式
1、余角关系
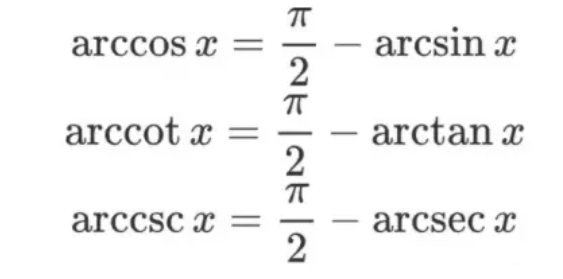
2、负数关系
arcsin ( − x ) = − arcsin x a r c c o s ( − x ) = π − arccos x a r c t a n ( − x ) = − arctan ( x ) arccot ( − x ) = π − arccot x arcsec ( − x ) = π − arcsec x a r c c o s ( − x ) = − arccos x \arcsin(-x)=-\arcsin x \\arccos(-x)=\pi-\arccos x \\arctan\left(-x\right)=-\arctan\left(x\right) \\\operatorname{arccot}(-x)=\pi-\operatorname{arccot}x \\\operatorname{arcsec}(-x)=\pi-\operatorname{arcsec}x \\arccos(-x)=-\arccos x arcsin(−x)=−arcsinxarccos(−x)=π−arccosxarctan(−x)=−arctan(x)arccot(−x)=π−arccotxarcsec(−x)=π−arcsecxarccos(−x)=−arccosx
三、极限公式
1、常见的极限公式
lim x → ∞ ( a x + b a x + c ) h x + k = e b − c a h \lim_{x\rightarrow\infty}(\frac{ax+b}{ax+c})^{hx+k}=e^{\frac{b-c}{a}h} x→∞lim(ax+cax+b)hx+k=eab−ch
2、等价无穷小
sin x ∼ x tan x ∼ x arcsin x ∼ x arctan x ∼ x 1 − cos x ∼ 1 2 x 2 ln ( 1 + x ) ∼ x e x − 1 ∼ x a x − 1 ∼ x ln a ( 1 + x ) ∂ − 1 ∼ ∂ x \begin{array}{ll}\sin x\sim x&\tan x\sim x\\\arcsin x\sim x&\arctan x\sim x\\1-\cos x\sim\frac{1}{2}x^{2}& \ln\left(1+x\right)\sim x \\ e^{x}-1\sim x\quad a^{x}-1\sim x\ln a &\left(1+x\right)^{\partial}-1\sim\partial x\end{array} sinx∼xarcsinx∼x1−cosx∼21x2ex−1∼xax−1∼xlnatanx∼xarctanx∼xln(1+x)∼x(1+x)∂−1∼∂x
3、泰勒公式
1 、 1 1 − x = 1 + x + x 2 + x 3 + x 4 + . . . + x n + . . . = ∑ n = 0 ∞ x n , x ∈ ( − 1 , 1 ) 2 、 1 1 + x = 1 − x + x 2 − x 3 + x 4 − . . . + ( − 1 ) n x n + . . . = ∑ n = 0 ∞ ( − 1 ) n x n , x ∈ ( − 1 , 1 ) 3 、 e x = 1 + x + x 2 2 ! + x 3 3 ! + x 4 4 ! + . . . + x n n ! + . . . = ∑ n = 0 ∞ x n n ! , x ∈ ( − ∞ , ∞ ) 4 、 sin x = x − x 3 3 ! + x 5 5 ! − x 7 7 ! + x 9 9 ! − . . . + ( − 1 ) n x 2 n + 1 ( 2 n + 1 ) ! + . . . = ∑ n = 0 ∞ ( − 1 ) n x 2 n + 1 ( 2 n + 1 ) ! , x ∈ ( − ∞ , ∞ ) 5 、 cos x = 1 − x 2 2 ! + x 4 4 ! − x 6 6 ! + x 8 8 ! − . . . + ( − 1 ) n x 2 n ( 2 n ) ! + . . = ∑ n = 0 ∞ ( − 1 ) n x 2 n ( 2 n ) ! , x ∈ ( − ∞ , ∞ ) 6 、 tan x = x + 1 3 x 3 + 2 15 x 5 + 17 315 x 7 + . . . = ∑ n = 0 ∞ B 2 n ( − 4 ) n ( 1 − 4 n ) ( 2 n ) ! x 2 n − 1 , x ∈ ( − π 2 , π 2 ) , B 2 n 是伯努利数 \begin{aligned}1、\frac{1}{1-x}& =1+x+x^2+x^3+x^4+...+x^n+...\\ & =\sum_{n=0}^\infty x^n\quad,\quad x\in(-1,1) \\2、\frac1{1+x}& =1-x+x^2-x^3+x^4-...+(-1)^nx^n+... \\ &=\sum_{n=0}^\infty(-1)^nx^n,x\in(-1,1) \\ 3、\quad e^x& =1+x+\frac{x^2}{2!}+\frac{x^3}{3!}+\frac{x^4}{4!}+...+\frac{x^n}{n!}+... \\ &=\sum_{n=0}^\infty\frac{x^n}{n!}\quad,\quad x\in(-\infty,\infty) \\ 4、\quad\sin x& =x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+\frac{x^9}{9!}-...+(-1)^n\frac{x^{2n+1}}{(2n+1)!}+... \\ &=\sum_{n=0}^\infty(-1)^n\frac{x^{2n+1}}{(2n+1)!}\quad,x\in(-\infty,\infty) \\ 5、\quad\cos x& =1-\frac{x^2}{2!}+\frac{x^4}{4!}-\frac{x^6}{6!}+\frac{x^8}{8!}-...+(-1)^n\frac{x^{2n}}{(2n)!}+.. \\ &=\sum_{n=0}^{\infty}(-1)^n\frac{x^{2n}}{(2n)!},x\in(-\infty,\infty) \\ 6、\quad\tan x& =x+\frac13x^3+\frac2{15}x^5+\frac{17}{315}x^7+... \\ &=\sum_{n=0}^{\infty}\frac{B_{2n}(-4)^n(1-4^n)}{(2n)!}x^{2n-1},x\in\left(-\frac{\pi}{2},\frac{\pi}{2}\right),B_{2n}\text{是伯努利数} \end{aligned} 1、1−x12、1+x13、ex4、sinx5、cosx6、tanx=1+x+x2+x3+x4+...+xn+...=n=0∑∞xn,x∈(−1,1)=1−x+x2−x3+x4−...+(−1)nxn+...=n=0∑∞(−1)nxn,x∈(−1,1)=1+x+2!x2+3!x3+4!x4+...+n!xn+...=n=0∑∞n!xn,x∈(−∞,∞)=x−3!x3+5!x5−7!x7+9!x9−...+(−1)n(2n+1)!x2n+1+...=n=0∑∞(−1)n(2n+1)!x2n+1,x∈(−∞,∞)=1−2!x2+4!x4−6!x6+8!x8−...+(−1)n(2n)!x2n+..=n=0∑∞(−1)n(2n)!x2n,x∈(−∞,∞)=x+31x3+152x5+31517x7+...=n=0∑∞(2n)!B2n(−4)n(1−4n)x2n−1,x∈(−2π,2π),B2n是伯努利数
7、 arcsinx = x + 1 2 x 3 3 + 1 × 3 2 × 4 x 5 5 + 1 × 3 × 5 2 × 4 × 6 x 7 7 + ⋯ + ( 2 n ) ! 2 2 n ( n ! ) 2 x 2 n + 1 2 n + 1 = x + x 3 6 + 3 x 5 40 + 5 x 7 112 + . . . = ∑ n = 0 ∞ ( 2 n ) ! 4 n ( n ! ) 2 x 2 n + 1 2 n + 1 , x ∈ [ − 1 , 1 ] 8 、 arctan x = x − x 3 3 + x 5 5 − ⋅ ⋅ ⋅ + ( − 1 ) n x 2 n + 1 2 n + 1 + ⋅ ⋅ ⋅ = ∑ n = 0 ∞ ( − 1 ) n x 2 n + 1 2 n + 1 , x ∈ [ − 1 , 1 ] 9 、ln ( 1 + x ) = x − x 2 2 + x 3 3 − ⋯ + ( − 1 ) n x n + 1 n + 1 + . . . = ∑ n = 0 ∞ ( − 1 ) n x n + 1 n + 1 , x ∈ ( − 1 , 1 ] 10 、 ( 1 + x ) α = 1 + α x + α ( α − 1 ) 2 ! x 2 + ⋅ ⋅ ⋅ + α ( α − 1 ) . . . ( α − n + 1 ) n ! x n + ⋅ ⋅ ⋅ = 1 + ∑ n = 1 ∞ α ( α − 1 ) ⋯ ( α − n + 1 ) n ! x n , x ∈ ( − 1 , 1 ) \begin{aligned} &\text{7、 arcsinx} =x+\frac{1}{2}\frac{x^{3}}{3}+\frac{1\times3}{2\times4}\frac{x^{5}}{5}+\frac{1\times3\times5}{2\times4\times6}\frac{x^{7}}{7}+\cdots+\frac{(2n)!}{2^{2n}(n!)^{2}}\frac{x^{2n+1}}{2n+1}\\&=x+\frac{x^3}6+\frac{3x^5}{40}+\frac{5x^7}{112}+...=\sum_{n=0}^{\infty}\frac{(2n)!}{4^n(n!)^2}\frac{x^{2n+1}}{2n+1},x\in[-1,1] \\ &8、\arctan x =x-\frac{x^3}3+\frac{x^5}5-\cdotp\cdotp\cdotp+\frac{(-1)^nx^{2n+1}}{2n+1}+\cdotp\cdotp\cdotp \\& =\sum_{n\operatorname{=}0}^\infty\frac{(-1)^nx^{2n+1}}{2n+1},x\in[-1,1] \\&9、\text{ln}(1+x) =x-\frac{x^2}2+\frac{x^3}3-\cdots+\frac{(-1)^nx^{n+1}}{n+1}+...\\& =\sum_{n\operatorname{=}0}^\infty(-1)^n\frac{x^{n+1}}{n+1},\quad x\in(-1,1] \\ &10、(1+x)^\alpha =1+\alpha x+\frac{\alpha\left(\alpha-1\right)}{2!}x^2+\cdotp\cdotp\cdotp+\frac{\alpha\left(\alpha-1\right)...\left(\alpha-n+1\right)}{n!}x^n+\cdotp\cdotp\cdotp \\&=1+\sum_{n=1}^{\infty}\frac{\alpha\left(\alpha-1\right)\cdots\left(\alpha-n+1\right)}{n!}x^{n},x\in(-1,1) \end{aligned} 7、 arcsinx=x+213x3+2×41×35x5+2×4×61×3×57x7+⋯+22n(n!)2(2n)!2n+1x2n+1=x+6x3+403x5+1125x7+...=n=0∑∞4n(n!)2(2n)!2n+1x2n+1,x∈[−1,1]8、arctanx=x−3x3+5x5−⋅⋅⋅+2n+1(−1)nx2n+1+⋅⋅⋅=n=0∑∞2n+1(−1)nx2n+1,x∈[−1,1]9、ln(1+x)=x−2x2+3x3−⋯+n+1(−1)nxn+1+...=n=0∑∞(−1)nn+1xn+1,x∈(−1,1]10、(1+x)α=1+αx+2!α(α−1)x2+⋅⋅⋅+n!α(α−1)...(α−n+1)xn+⋅⋅⋅=1+n=1∑∞n!α(α−1)⋯(α−n+1)xn,x∈(−1,1)