PyTorch -- RNN 快速实践

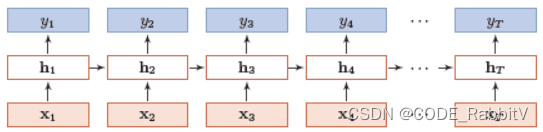
RNN Layer torch.nn.RNN(input_size,hidden_size,num_layers,batch_first)
- input_size: 输入的编码维度
- hidden_size: 隐含层的维数
- num_layers: 隐含层的层数
- batch_first: ·True 指定输入的参数顺序为：
  - x： $batch, seq_len, input_size$
  - h0： $batch, num_layers, hidden_size$
RNN 的输入：
- x：seq_len, batch, input_size
  - seq_len: 输入的序列长度
  - batch: batch size 批大小
- h0： $num_layers, batch, hidden_size$
RNN 的输出：
- y: $seq_len, batch, hidden_size$

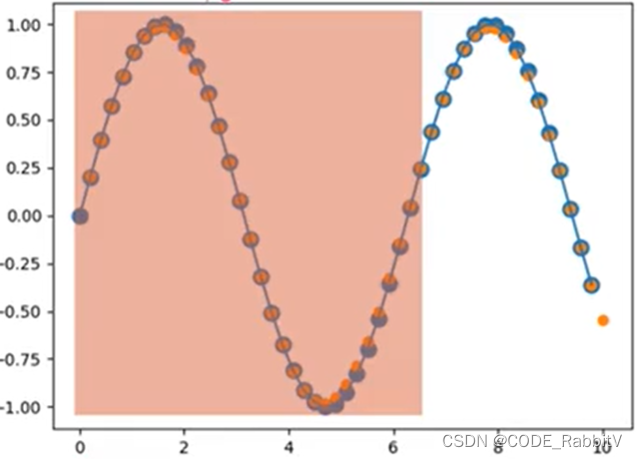
实战之预测 正弦曲线：以下会以此为例，演示 RNN 预测任务的部署

步骤一：确定 RNN Layer 相关参数值并基于此创建 Net

python3 复制代码

import numpy as np
from matplotlib import pyplot as plt

import torch
import torch.nn as nn
import torch.optim as optim


seq_len     = 50
batch       = 1
num_time_steps = seq_len

input_size  = 1
output_size = input_size
hidden_size = 10  	
num_layers = 1  	
batch_first = True 

class Net(nn.Module):  ## model 定义
	def __init__(self):
		super(Net, self).__init__()
		self.rnn = nn.RNN(
		input_size=input_size,
		hidden_size=hidden_size,
		num_layers=num_layers,
		batch_first=batch_first)
		# for p in self.rnn.parameters():
		# 	nn.init.normal_(p, mean=0.0, std=0.001)
		self.linear = nn.Linear(hidden_size, output_size)

	def forward(self, x, hidden_prev):
		out, hidden_prev = self.rnn(x, hidden_prev)
		# out: [batch, seq_len, hidden_size]
		out = out.view(-1, hidden_size)  # [batch*seq_len, hidden_size]
		out = self.linear(out) 			 # [batch*seq_len, output_size]
		out = out.unsqueeze(dim=0)    # [1, batch*seq_len, output_size]
		return out, hidden_prev

步骤二：确定训练流程

python3 复制代码

lr=0.01

def tarin_RNN():
    model = Net()
    print('model:\n',model)
    criterion = nn.MSELoss()
    optimizer = optim.Adam(model.parameters(), lr)
    hidden_prev = torch.zeros(num_layers, batch, hidden_size)  #初始化h

    l = []
    for iter in range(100):  # 训练100次
        start = np.random.randint(10, size=1)[0]  ## 序列起点
        time_steps = np.linspace(start, start+10, num_time_steps)  ## 序列
        data = np.sin(time_steps).reshape(num_time_steps, 1)  ## 序列数据

        x = torch.tensor(data[:-1]).float().view(batch, seq_len-1, input_size)
        y = torch.tensor(data[1: ]).float().view(batch, seq_len-1, input_size)  # 目标为预测一个新的点

        output, hidden_prev = model(x, hidden_prev)
        hidden_prev = hidden_prev.detach()  ## 最后一层隐藏层的状态要 detach

        loss = criterion(output, y)
        model.zero_grad()
        loss.backward()
        optimizer.step()

        if iter % 100 == 0:
            print("Iteration: {} loss {}".format(iter, loss.item()))
            l.append(loss.item())
    #############################绘制损失函数#################################
    plt.plot(l,'r')
    plt.xlabel('训练次数')
    plt.ylabel('loss')
    plt.title('RNN LOSS')
    plt.savefig('RNN_LOSS.png')
    return hidden_prev,model

 hidden_prev,model = tarin_RNN()

步骤三：测试训练结果

python3 复制代码

start = np.random.randint(3, size=1)[0]  ## 序列起点
time_steps = np.linspace(start, start+10, num_time_steps)  ## 序列
data = np.sin(time_steps).reshape(num_time_steps, 1)  ## 序列数据
x = torch.tensor(data[:-1]).float().view(batch, seq_len-1, input_size)
y = torch.tensor(data[1: ]).float().view(batch, seq_len-1, input_size)  # 目标为预测一个新的点    

predictions = []  ## 预测结果
input = x[:,0,:]
for _ in range(x.shape[1]):
    input = input.view(1, 1, 1)
    pred, hidden_prev = model(input, hidden_prev)
    input = pred  ## 循环获得每个input点输入网络
    predictions.append(pred.detach().numpy()[0])
x= x.data.numpy()
y = y.data.numpy( )
plt.scatter(time_steps[:-1], x.squeeze(), s=90)
plt.plot(time_steps[:-1], x.squeeze())
plt.scatter(time_steps[1:],predictions)  ## 黄色为预测
plt.show()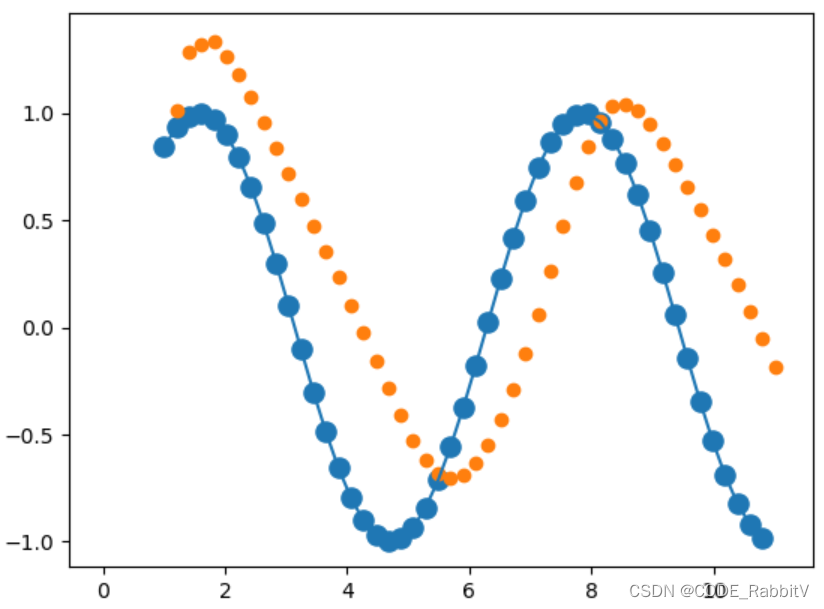

【高阶】上述例子比较简单，便于入门以推理到自己的目标任务，实际 RNN 训练可能更有难度，可以添加

对于梯度爆炸的解决：

python3 复制代码

for p in model.parameters()"
	p.grad.nomr()
	torch.nn.utils.clip_grad_norm_(p， 10)  ## 其中的 norm 后面的_ 表示 in place

对于梯度消失的解决：-> LSTM

另一个很好的实例关于飞行轨迹预测- - RNN-博客链接，可供学习参考
B站视频参考资料