一、查询优化的核心定位与流程
1. 核心定义
查询优化是数据库管理系统(DBMS)将 SQL 查询转换为高效执行计划的关键过程,通过调整查询逻辑结构、选择最优操作策略、确定执行顺序,在不改变查询结果的前提下最小化执行开销(CPU、I/O 等)。
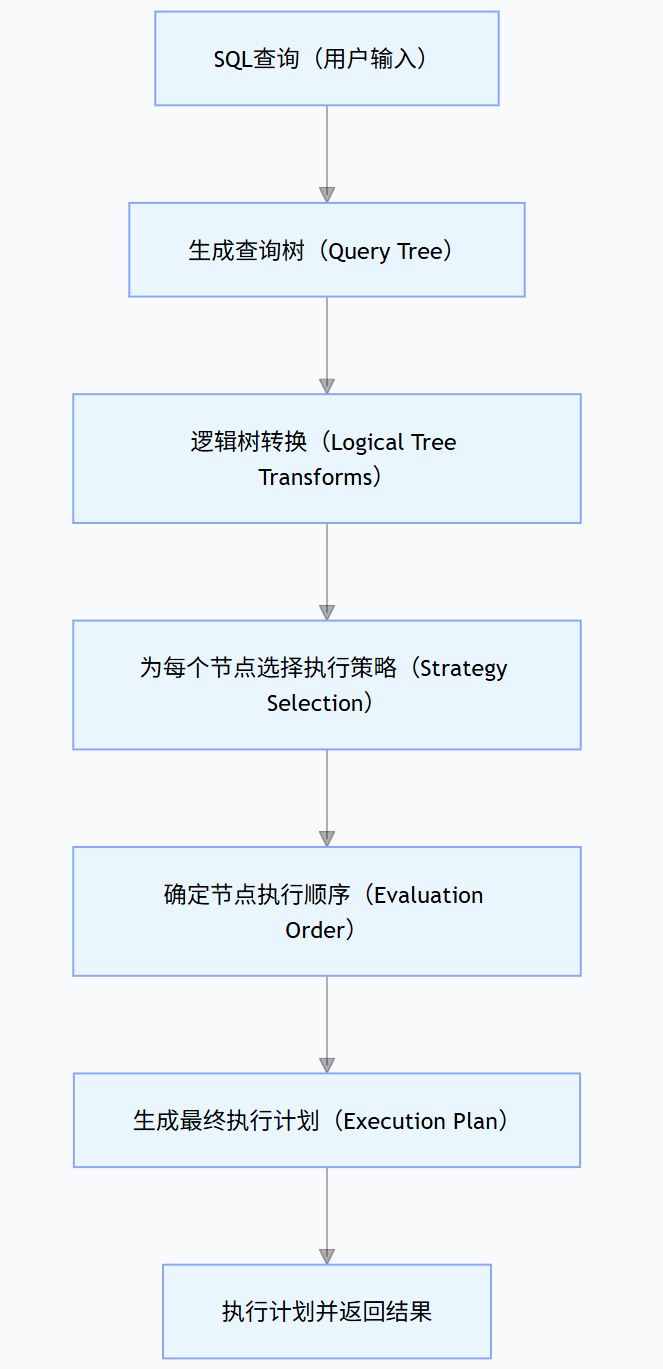
2. 完整流程(从 SQL 到执行计划)
SQL查询(用户输入)
生成查询树(Query Tree)
逻辑树转换(Logical Tree Transforms)
为每个节点选择执行策略(Strategy Selection)
确定节点执行顺序(Evaluation Order)
生成最终执行计划(Execution Plan)
执行计划并返回结果
SQL查询(用户输入)
生成查询树(Query Tree)
逻辑树转换(Logical Tree Transforms)
为每个节点选择执行策略(Strategy Selection)
确定节点执行顺序(Evaluation Order)
生成最终执行计划(Execution Plan)
执行计划并返回结果
- 核心目标:在保证结果正确性的前提下,降低查询的总计算成本(尤其是空间查询的 CPU 和 I/O 双重开销)。
二、核心基础:查询树(Query Tree)
1. 定义与结构
- 查询树是 SQL 查询的可视化表示,用于拆解查询的逻辑结构:
- 节点(Nodes):对应查询的构建块(如选择、连接、投影等操作);
- 子节点(Children):对应某一操作的输入数据;
- 叶子节点(Leafs):对应查询涉及的基础数据表。
2. 示例(空间查询)
SQL 查询:
sql
Select L.Name
From Lake L, Facilities Fa
Where ST_Area(L.Geometry) > 20 and
Fa.Name = 'Campground' and
ST_Distance(Fa.Geometry, L.Geometry) < 50对应的查询树结构:
plaintext
L.Name(投影操作)
|
ST_Distance(Fa.Geom, L.Geom) < 50(空间连接操作)
/ \
ST_Area(L.Geom) > 20(选择操作) Fa.Name = 'Campground'(选择操作)
/ \
Lake L(表) Facilities Fa(表)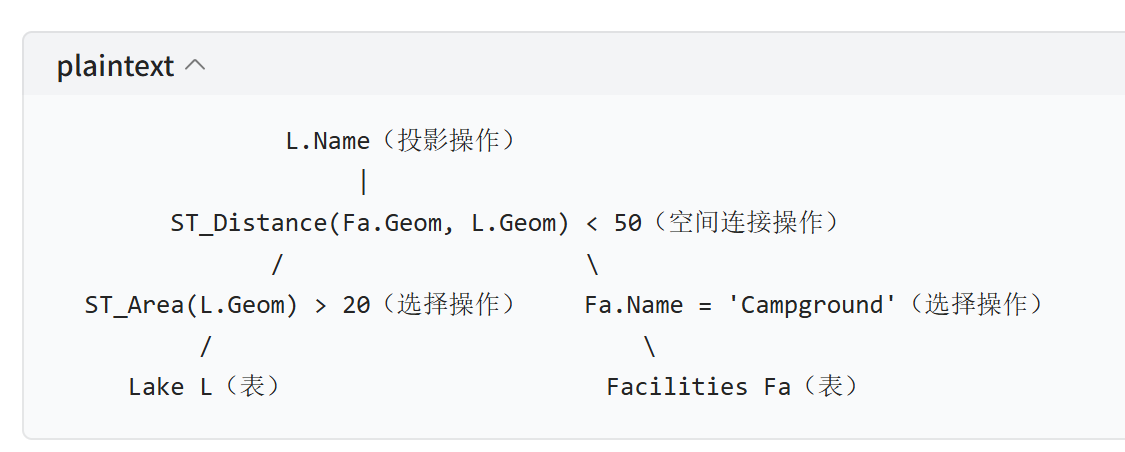
三、关键步骤 1:查询树的逻辑转换(Logical Tree Transforms)
1**. 转换核心原则**
- 等价转换:不改变查询结果;
- 成本优化:通过调整查询树结构,减少子查询输出数据量、降低父节点计算压力。
2. 经典转换操作
| 转换类型 | 操作逻辑 | 优化效果 |
|---|---|---|
| 选择操作下推(Push down select) | 将 "选择" 节点移动到 "连接" 节点下方,先过滤数据再执行连接 | 减少连接操作的输入数据量,降低连接开销 |
| 投影操作下推(Push down project) | 将 "投影" 节点(只保留需要的列)下移,尽早剔除无用属性 | 减少数据传输和存储的开销 |
| 连接顺序重排(Reorder join operations) | 调整多个表的连接顺序(如小表先连接) | 降低中间结果集的大小,减少后续计算压力 |
3. 空间查询的特殊考量
传统逻辑转换规则(适用于非空间查询)需调整,核心原因:
- 非空间查询:I/O 开销占主导,CPU 开销可忽略;
- 空间查询:CPU 开销(如几何计算)与 I/O 开销并重,复杂空间操作(如
ST_Area)可能比连接操作(如ST_Distance)成本更高。
示例:空间选择操作下推的风险
- 若
ST_Area(L.Geom) > 20的计算成本高于ST_Distance的连接成本,将该选择操作下推可能导致总开销增加,需结合成本模型判断。
四、关键步骤 2:执行计划的构成
一个完整的执行计划包含 3 个核心组件:
- 优化后的查询树:经过逻辑转换的查询结构;
- 每个非叶节点的执行策略:为每个操作(如选择、连接)指定具体实现方式(如扫描、索引查询、空间分区连接等);
- 非叶节点的执行顺序:确定各操作的执行先后(如先执行选择再执行连接)。
示例(空间查询执行计划)
- 查询树节点策略:
ST_Area(L.Geom) > 20:采用全表扫描(Scan);Fa.Name = 'Campground':采用索引查询(Index);ST_Distance(Fa.Geom, L.Geom) < 50:采用空间分区连接(Space-Partitioning Join);L.Name:采用即时投影(On-the-fly Projection);
- 执行顺序:先执行两个选择操作,再执行空间连接,最后执行投影。
五、关键步骤 3:构建块的策略选择(Strategy Selection)
为查询树中每个操作节点选择最优实现策略,核心方法分为 3 类:
1. 优先级方案(Priority Scheme)
- 逻辑:预先定义策略优先级,根据数据结构和索引的可用性,选择优先级最高的适用策略;
- 优势:速度快,适用于复杂查询;
- 示例:优先选择索引查询,无索引时选择全表扫描。
2. 基于规则的方法(Rule Based Approach)
- 逻辑:系统内置一组规则,映射 "场景→策略",根据查询场景自动匹配策略;
- 规则示例:若范围查询的结果集大小超过数据文件的 2%,则选择全表扫描而非索引查询;
- 适用场景:空间查询(因空间策略的成本模型不成熟,商用 SDBMS 常采用)。
3. 基于成本的方法(Cost Based Approach)
- 核心逻辑:通过成本模型估算每种策略的开销,选择总成本最低的策略(关系数据库的主流方法)。
(1)成本模型的核心参数(关系数据库)
针对非空间查询,成本模型主要关注 I/O 开销(假设读取 1 个数据块的成本为 1),核心参数包括:
| 参数 | 定义 |
|---|---|
| T(R) | 表 R 的记录行数 |
| B(R) | 表 R 的数据块数量 |
| V(R, A) | 表 R 中属性 A 的不同取值个数(基数) |
| 选择性因子(Selectivity) | 满足查询条件的记录占比(如σ_{A=a}(R)的选择性为1/V(R, A)) |
(2)常见操作的成本计算公式
| 操作类型 | 场景 | 成本公式 |
|---|---|---|
| 选择(σ) | 堆文件(无索引) | B(R) |
| 选择(σ) | 聚集索引(有序文件) | B (R) * 选择性因子 |
| 选择(σ) | 非聚集索引 | T (R) * 选择性因子 |
| 嵌套循环连接(R⋈S) | 无索引(内存 2 个数据块) | B(R) + B(R)*B(S) |
| 嵌套循环连接(R⋈S) | S 的属性 B 有聚集索引 | B(R) + T(R)*B(S)/V(S, B) |
| 哈希连接(R⋈S) | - | B(R) + B(S) |
(3)空间查询的成本模型挑战
- 空间查询是 CPU 和 I/O 双密集型,需同时考虑两者开销;
- 空间操作(如
ST_Distance、ST_Within)的成本难以精准估算(如ST_Distance的估算成本为 10000,ST_Boundary为 500); - 成本模型不成熟,商用 SDBMS 多结合规则和成本模型使用。
(4)成本计算示例(关系连接查询)
已知表 R (A,B)、S (B,C)、T (C,D) 的统计信息:
- T(R)=10⁵,B(R)=100;T(S)=6×10⁶,B(S)=3000;T(T)=5×10⁴,B(T)=40000;
- V(R,A)=5×10⁴,V(R,B)=V(S,B)=3×10³,V(S,C)=V(T,C)=2×10⁴;
- 索引:R.A(聚集)、S.B(聚集)、T.C(聚集)。
查询:Select D from R,S,T where R.A=2432 and R.B=S.B and S.C=T.C and T.D=1234成本计算:
- 选择 R.A=2432:成本 = B (R)/V (R,A)=100/5×10⁴=0.002→取整为 1;
- 连接 R⋈S(R.B=S.B):成本 = T (R)×B (S)/V (S,B)=10⁵×3000/3×10³=10⁵;
- 连接(R⋈S)⋈T(S.C=T.C):成本 = T (S)×B (T)/V (T,C)=6×10⁶×40000/2×10⁴=1.2×10⁷;
- 选择 T.D=1234:成本 = B (T)/V (T,D)=40000/10⁴=4;
- 总成本≈1+10⁵+1.2×10⁷+4=12100005。
六、空间查询优化的特殊要点
1. 核心差异(与非空间查询)
- 成本构成:CPU 开销(几何计算)不可忽略,需平衡 CPU 和 I/O 成本;
- 逻辑转换:空间选择操作下推需谨慎,避免因高 CPU 成本的空间操作提前执行导致总开销增加;
- 策略选择:依赖规则 - based 方法,结合空间索引(如 R 树)和过滤 - 精炼范式优化。
2. 典型空间操作的成本示例(PostGIS)
| 空间函数 | 估算成本 | 说明 |
|---|---|---|
| ST_Distance(geom1, geom2) | 10000 | 计算两个几何对象的距离,CPU 开销高 |
| ST_Boundary(geom) | 500 | 获取几何对象的边界,CPU 开销较低 |
3. 空间查询优化示例(PostGIS 执行计划对比)
查询:select C.name, count(*) from ne_10m_admin_0_countries C, ne_10m_populated_places P where ST_Within(P.geom, C.geom) group by C.name
| 执行计划 | 策略 | 总成本 | 核心优化点 |
|---|---|---|---|
| 未加索引 | 嵌套循环 + 全表扫描 | 497105.20 | 无索引,需遍历所有表数据对 |
| 加空间索引(icity) | 嵌套循环 + 索引扫描 | 1411.56 | 利用空间索引过滤无效数据,大幅降低 I/O 和 CPU 开销 |
七、查询优化总结
1. 核心流程
SQL 查询 → 生成查询树 → 逻辑树转换 → 策略选择 → 确定执行顺序 → 生成执行计划 → 执行并返回结果。
2. 关键技术
- 逻辑转换:选择 / 投影下推、连接顺序重排;
- 策略选择:优先级方案、规则 - based、成本 - based;
- 空间查询特殊优化:过滤 - 精炼范式、空间索引、平衡 CPU 与 I/O 成本。
3. 空间查询优化核心难点
- 成本模型不成熟:空间操作的 CPU 和 I/O 成本难以精准估算;
- 逻辑转换需适配:空间选择下推可能增加总开销,需结合场景判断;
- 策略选择依赖索引:空间索引(如 R 树)是提升优化效果的关键。
八、有哪些常见的空间查询优化技术?
常见的空间查询优化技术围绕 "降低计算开销、减少无效数据处理" 核心目标,结合空间数据的几何特性(如位置、形状)和空间查询的 "过滤 - 精炼" 范式展开,覆盖索引设计、查询逻辑优化、执行策略选择等多个层面。以下是核心技术分类及具体实现:
一、基于索引的优化技术(降低 I/O 与筛选开销)
空间索引是空间查询优化的 "基石",通过对空间对象的近似形状(如 MBR)或位置编码建立索引,快速过滤无效数据,减少后续精确计算的对象数量。
1. 主流空间索引类型及应用场景
| 索引类型 | 核心原理 | 适用查询场景 | 优势 |
|---|---|---|---|
| R 树(R-Tree) | 以 "最小正交包围盒(MBR)" 为核心,按空间邻近性组织数据,形成层次化树结构 | 范围查询(如 "某区域内的医院")、空间连接(如 "与河流相交的省份")、最近邻查询 | 支持动态数据更新,适配复杂空间对象(线、多边形) |
| R树(R-Tree) | R 树的改进版,通过优化节点分裂策略减少 MBR 重叠,提升查询效率 | 高维空间数据、密集型空间查询 | 比 R 树减少 "假阳性" 候选集,过滤效果更优 |
| Z-Order / 希尔伯特曲线(空间填充曲线) | 将二维 / 高维空间位置映射为一维整数(编码),利用 B + 树索引一维编码 | 点查询(如 "经纬度定位街道")、范围查询 | 复用传统 B + 树索引技术,适配需有序存储的场景 |
| 网格索引(Grid Index) | 将空间划分为规则网格,每个网格对应一个索引项,存储网格内的空间对象 | 大范围、低精度的范围查询(如 "某行政区划内的地块") | 结构简单、查询速度快,适合静态数据 |
2. 索引优化实践
- 索引选择性适配:对高频查询字段(如 "行政区边界""道路线")优先建立索引,对低频或小表可省略索引(避免索引维护开销);
- 索引与过滤步结合:在过滤步中直接利用索引快速定位 MBR 满足条件的对象,避免全表扫描(如 R 树索引加速 "MBR 重叠判断");
- 索引缓存:将高频访问的索引节点(如 R 树的根节点、中间节点)缓存到内存,减少磁盘 I/O(索引节点通常较小,缓存效率高)。
二、查询逻辑优化技术(减少计算量与数据传输)
通过调整查询的逻辑结构,在不改变结果的前提下,提前过滤无效数据、简化计算步骤,降低后续执行压力。
1. 选择 / 投影操作下推(Push-Down Optimization)
- 核心逻辑:将 "选择"(过滤条件)或 "投影"(仅保留必要字段)操作尽可能提前执行,减少进入后续连接、排序等操作的数据量;
- 空间查询适配 :
- 非空间过滤优先:先执行非空间条件(如 "设施类型 = 医院"),再执行空间条件(如 "距离某点 10km 内"),减少空间计算的对象数量;
- 空间选择谨慎下推:若空间操作(如
ST_Area计算多边形面积)的 CPU 成本高于后续连接操作(如ST_Distance),则不盲目下推(需结合成本模型判断)。
2. 连接顺序优化(Join Order Optimization)
- 核心逻辑:调整多表连接的顺序,优先连接小表或过滤后结果集小的表,减少中间结果集大小;
- 空间连接场景 :
- 示例:查询 "与湖泊重叠且位于某城市内的公园",优先执行 "公园∩城市"(过滤掉城市外的公园),再与湖泊执行空间连接,避免大量无效的 "公园 - 湖泊" 配对计算;
- 原则:"小结果集驱动大结果集",即先处理过滤后数据量少的表,再与另一表连接。
3. 空间谓词重写(Predicate Rewriting)
- 核心逻辑:将复杂空间谓词转换为等价但计算成本更低的形式;
- 常见场景 :
- 用 "MBR 包含" 替代 "精确包含":在过滤步中,用
MBR(A)包含MBR(B)近似A包含B,快速排除明显不满足的对象; - 距离条件转换:将 "点 A 到线 B 的距离<500m" 转换为 "点 A 的 MBR 与线 B 的 500m 缓冲 MBR 重叠",减少精确距离计算(缓冲 MBR 可预计算存储)。
- 用 "MBR 包含" 替代 "精确包含":在过滤步中,用
三、执行策略优化技术(提升计算效率)
针对空间查询的四大核心构建块(点查询、范围查询、最近邻查询、空间连接),选择最优执行策略,平衡 CPU 与 I/O 开销。
1. 点查询优化策略
- 全表扫描:仅适用于小表(如少于 1000 条记录的 "景区点位表"),无索引时的兜底方案;
- 索引查询:优先选择 R 树或 Z-Order+B + 树索引,直接定位目标位置所在的数据块(如通过 R 树索引查询 "某经纬度对应的 POI",仅访问 1-2 个数据块);
- 空间编码匹配:利用 Z-Order 编码的一维特性,通过二分查找快速定位目标编码对应的空间对象。
2. 范围查询优化策略
- 索引驱动查询:通过 R 树索引遍历所有与查询范围 MBR 重叠的节点,筛选候选集(如查询 "某矩形区域内的商铺",R 树索引可快速排除区域外的节点);
- 空间填充曲线区间扫描:将查询范围映射为 Z-Order 编码的连续区间,通过 B + 树索引定位区间起始位置,再向前扫描至区间结束(避免全表遍历);
- 多区间合并:若查询范围对应多个不连续的 Z-Order 区间,合并相邻区间减少扫描次数(如将 [6-7] 和 [12-13] 两个区间合并为两次扫描,而非多次独立扫描)。
3. 最近邻查询优化策略
- 两阶段法(Two-Phase Approach) :
- 点查询定位查询点所在的数据块,计算该块内对象与查询点的最小距离 M;
- 范围查询以 M 为半径筛选对象,精确计算距离后确定最近邻(避免全局距离计算);
- R 树单阶段递归法 :
- 从 R 树根节点开始,计算各子节点与查询点的 "最小可能距离" 和 "最大可能距离";
- 剔除被其他节点 "支配" 的子节点(如节点 A 的最大距离<节点 B 的最小距离,则 B 不可能包含最近邻),递归遍历剩余节点直至叶子节点(减少无效节点访问)。
4. 空间连接优化策略
- 带索引的嵌套循环连接 :
- 外循环遍历小表(如 "消防站表"),内循环通过空间索引(如 R 树)查询与外循环对象满足条件的大表对象(如 "500m 内的房屋"),避免全表嵌套循环(内循环开销从 O (N) 降至 O (logN));
- 空间分区连接(Space-Partitioning Join) :
- 将空间划分为多个分区(如按行政区划、网格),仅对同一分区内的对象对执行连接(如 "非洲的河流仅与非洲的国家连接"),减少跨分区的无效配对;
- 树匹配连接(Tree-Matching Join) :
- 若两个表均有 R 树索引,从根节点开始递归遍历两棵树,仅对 MBR 重叠的节点对继续深入,直至叶子节点(如 "河流 R 树" 与 "省份 R 树" 的节点匹配,减少对象级别的配对计算)。
四、数据预处理与存储优化技术(从源头降低开销)
通过数据存储结构调整和预处理,减少查询时的计算与 I/O 成本。
1. 空间数据近似存储(MBR 预计算)
- 核心:对复杂空间对象(如多边形、线串),预计算并存储其 MBR,避免查询时动态计算;
- 应用:过滤步直接使用预存的 MBR 进行重叠判断,减少 CPU 开销(MBR 获取成本≈1,远低于精确几何计算成本≈100);
- 示例:在 "省份表" 中存储每个省份的 MBR,查询 "与某铁路相交的省份" 时,先通过 MBR 快速排除不相交的省份。
2. 数据分区存储(Spatial Partitioning)
- 按空间位置分区:将空间数据按地理区域(如行政区划、网格)拆分存储,查询时仅加载目标分区的数据(如 "查询北京市的道路",仅加载 "北京分区" 的道路数据,而非全国道路数据);
- 按数据类型分区:将点、线、面等不同类型的空间数据分开存储(如 "POI 点位表""道路线表""地块多边形表"),避免查询时加载无关类型数据。
3. 冗余存储高频计算结果
- 对高频使用的空间计算结果(如 "城市的面积""河流的长度"),提前计算并作为字段存储在表中,避免查询时重复计算;
- 示例:在 "湖泊表" 中冗余存储
lake_area(预计算的面积),查询 "面积>100km² 的湖泊" 时,直接读取lake_area字段,无需调用ST_Area函数动态计算。
五、成本模型与策略自适应优化(动态选择最优方案)
通过成本模型估算不同策略的开销,结合数据特征动态选择最优执行方案,避免 "一刀切" 的策略选择。
1. 成本模型核心维度
空间查询的成本模型需同时考虑I/O 成本 (数据块读取次数)和CPU 成本(几何计算次数),核心参数包括:
- I/O 相关:表数据块数量(B (R))、索引深度、缓存命中率;
- CPU 相关:空间操作类型(如
ST_Distance比ST_Within成本高)、候选集大小(假阳性比例)、几何对象复杂度(如多边形顶点数越多,计算成本越高)。
2. 策略自适应选择示例
- 范围查询:若查询范围小(如 "500m 半径"),选择 R 树索引(I/O 和 CPU 成本低);若查询范围大(如 "整个省份"),选择全表扫描(索引过滤优势不明显,避免索引遍历开销);
- 空间连接:若两个表均有 R 树索引且连接条件选择性高(如 "重叠的河流与省份"),选择树匹配连接;若仅一个表有索引,选择带索引的嵌套循环连接;若均无索引且数据量小,选择普通嵌套循环连接。
总结
空间查询优化技术的核心逻辑是 "尽早过滤、减少计算、适配场景":
- 用索引和 MBR 实现 "粗过滤",减少候选集大小;
- 用查询逻辑优化(下推、连接重排)减少中间数据量;
- 用自适应执行策略平衡 CPU 与 I/O 开销;
- 用数据预处理(预计算、分区)从源头降低查询成本。
实际应用中需结合具体场景(如查询类型、数据量、索引情况)选择组合技术,例如 "R 树索引 + 选择下推 + 空间分区连接" 可高效处理复杂的空间连接查询,而 "Z-Order 索引 + 点查询策略" 适合高频的位置定位场景。