通过对滚动轴承故障诊断研究现状及稀疏表示方法在滚动轴承故障诊断领域中应用现状的调研,发现稀疏表示方法与故障特征提取和故障分类的关联,针对故障诊断问题,通过构造合理的故障稀疏表示模型,选取适合的模型优化算法,构造和故障信号相匹配的字典,可以实现故障特征提取问题和故障分类问题的有效解决。然而,稀疏表示方法应用于故障诊断仍存在诸多亟待解决的关键问题,主要归纳为:
(1)稀疏系数缺乏有效性当前基于稀疏表示的故障特征提取方法,对于建立的故障稀疏表示模型,在稀疏系数的求解过程中参数设置多采用固定值,对于不同类型故障信号缺乏自适应性,造成求解出的不同类型故障信号的稀疏系数稀疏度差异很大,甚至出现欠稀疏和过稀疏问题,降低了稀疏系数的有效性。此外,当前大多数基于稀疏表示的故障特征提取方法,在稀疏系数的求解过程中,更多关注的是稀疏系数的稀疏性,而忽略了故障特征提取之后要进行故障分类,有可能造成即使稀疏系数具有较好的稀疏性,然而提取出的不同类型故障特征信号的可区分性并不强,基于这样的稀疏系数重构出的故障特征信号,故障分类能力将会降低。
(2)字典构造存在局限性稀疏系数的求解是建立在字典已知的基础上,根据现有信号处理方法的变换函数基构造稀疏表示字典是一种常用构造字典的方法,然而直接采用标准固定变换函数基,常缺乏对故障信号内在结构以及信号特征等先验信息的考虑,会影响稀疏系数对故障信号的表征能力。此外,当前基于稀疏表示的故障分类方法,通常直接采用训练样本构造固定分类字典,不仅构造原子受噪声干扰严重,而且分类字典固定,对待分类样本缺乏自适应性,致使分类精度降低。
(3)稀疏模型优化算法中关键参数设置多依赖于经验值的缺陷稀疏模型优化算法中关键正则化参数设置将直接决定稀疏系数的选取,当前方法多依赖于经验值。然而,稀疏模型在实际解决故障诊断问题的过程中,会涉及处理包含不同类型的故障信号,基于经验值设置正则化参数,不仅缺乏准确性而且缺乏自适应性。
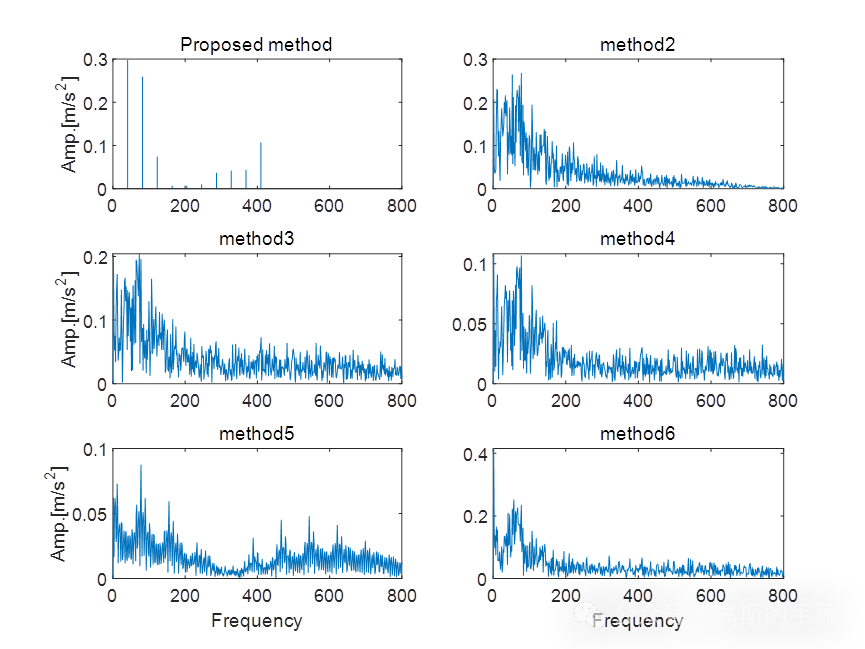
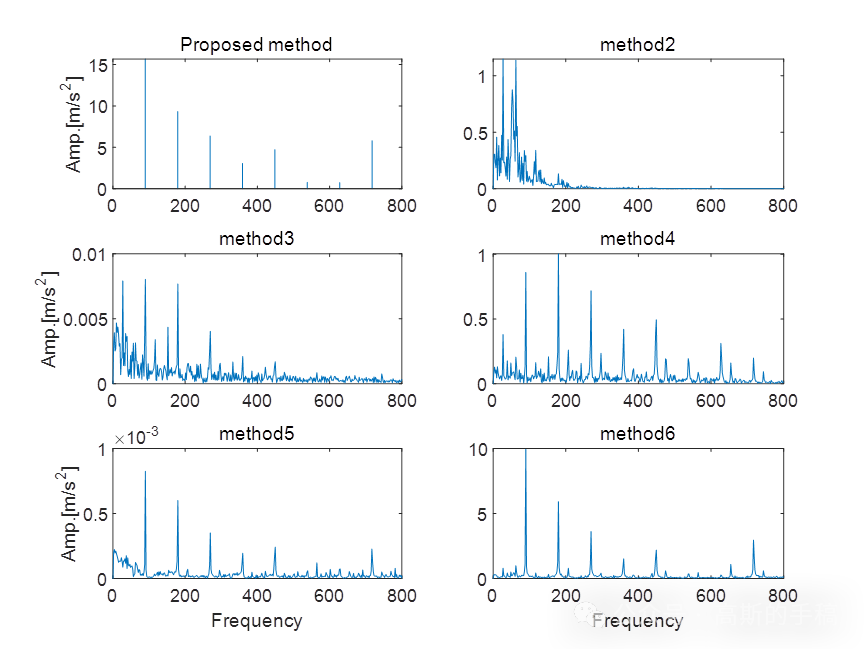
鉴于此,采用一种改进稀疏学习信号处理方法对滚动轴承进行故障诊断,运行环境为MATLAB。
Matlab
function w = tqwt(x,Q,r,J)
% w = tqwt(x,Q,r,J)
% Tunable Q-factor wavelet transform (TQWT)
% INPUT
% x - input signal (even length)
% Q - Q-factor
% r - oversampling rate (redundancy)
% J - number of levels
% OUTPUT
% w - wavelet coefficients
% NOTES
% w{j} is subband j for j = 1,...,J+1
% w{1} is the highest-frequency subband signal
% w{J+1} is the low-pass subband signal
%
% % Example (verify perfect reconstruction)
% Q = 4; r = 3; J = 3; % parameters
% N = 200; % signal length
% x = rand(1,N); % test signal
% w = tqwt(x,Q,r,J); % wavelet transform
% y = itqwt(w,Q,r,N); % inverse wavelet transform
% max(abs(x - y)) % reconstruction error
check_params(Q,r,J);
beta = 2/(Q+1);
alpha = 1-beta/r;
N = length(x);
Jmax = floor(log(beta*N/8)/log(1/alpha));
if J > Jmax
J = Jmax;
fprintf('Note: too many levels specified.\n')
if Jmax > 0
fprintf('Reduce levels to %d\n',Jmax);
else
fprintf('Increase signal length.\n');
end
w = [];
return
end
X = uDFT(x);
w = cell(1, J+1);
% J stages:
for j = 1:J
N0 = 2*round(alpha^j * N/2);
N1 = 2*round(beta * alpha^(j-1) * N/2);
[X, W] = afb(X, N0, N1);
w{j} = uDFTinv(W);
end
w{J+1} = uDFTinv(X);
完整代码可通过知乎学术咨询获得:https://www.zhihu.com/consult/people/792359672131756032?isMe=1
擅长领域:现代信号处理,机器学习,深度学习,数字孪生,时间序列分析,设备缺陷检测、设备异常检测、设备智能故障诊断与健康管理PHM等。