算法训练与程序竞赛题目集合（L2）

[L2-001 城市间紧急救援](#L2-001 城市间紧急救援)

输入格式:

输出格式:

输入样例:

输出样例:

[L2-002 链表去重](#L2-002 链表去重)

[L2-003 月饼](#L2-003 月饼)

[L2-004 这是二叉搜索树吗？](#L2-004 这是二叉搜索树吗？)

输入格式：

输出格式：

[输入样例 1：](#输入样例 1：)

[输出样例 1：](#输出样例 1：)

[输入样例 2：](#输入样例 2：)

[输出样例 2：](#输出样例 2：)

[输入样例 3：](#输入样例 3：)

[输出样例 3：](#输出样例 3：)

[L2-005 集合相似度](#L2-005 集合相似度)

[L2-006 树的遍历](#L2-006 树的遍历)

[L2-007 家庭房产](#L2-007 家庭房产)

[L2-008 最长对称子串](#L2-008 最长对称子串)

[L2-009 抢红包](#L2-009 抢红包)

[L2-010 排座位](#L2-010 排座位)

[L2-011 玩转二叉树](#L2-011 玩转二叉树)

[L2-012 关于堆的判断](#L2-012 关于堆的判断)

[L2-013 红色警报](#L2-013 红色警报)

[L2-014 列车调度](#L2-014 列车调度)

[L2-015 互评成绩](#L2-015 互评成绩)

[L2-016 愿天下有情人都是失散多年的兄妹](#L2-016 愿天下有情人都是失散多年的兄妹)

[L2-017 人以群分](#L2-017 人以群分)

[L2-018 多项式A除以B](#L2-018 多项式A除以B)

[L2-019 悄悄关注](#L2-019 悄悄关注)

[L2-020 功夫传人](#L2-020 功夫传人)

[L2-021 点赞狂魔](#L2-021 点赞狂魔)

[L2-022 重排链表](#L2-022 重排链表)

[L2-023 图着色问题](#L2-023 图着色问题)

[L2-024 部落](#L2-024 部落)

[L2-025 分而治之](#L2-025 分而治之)

[L2-026 小字辈](#L2-026 小字辈)

[L2-027 名人堂与代金券](#L2-027 名人堂与代金券)

[L2-028 秀恩爱分得快](#L2-028 秀恩爱分得快)

输入格式：

输出格式：

[输入样例 1：](#输入样例 1：)

[输出样例 1：](#输出样例 1：)

[输入样例 2：](#输入样例 2：)

[输出样例 2：](#输出样例 2：)

[L2-029 特立独行的幸福](#L2-029 特立独行的幸福)

输入格式：

输出格式：

[输入样例 1：](#输入样例 1：)

[输出样例 1：](#输出样例 1：)

[输入样例 2：](#输入样例 2：)

[输出样例 2：](#输出样例 2：)

[L2-030 冰岛人](#L2-030 冰岛人)

[L2-031 深入虎穴](#L2-031 深入虎穴)

[L2-032 彩虹瓶](#L2-032 彩虹瓶)

[L2-033 简单计算器](#L2-033 简单计算器)

输入格式：

输出格式：

[输入样例 1：](#输入样例 1：)

[输出样例 1：](#输出样例 1：)

[输入样例 2：](#输入样例 2：)

[输出样例 2：](#输出样例 2：)

[L2-034 口罩发放](#L2-034 口罩发放)

[L2-035 完全二叉树的层序遍历](#L2-035 完全二叉树的层序遍历)

[L2-036 网红点打卡攻略](#L2-036 网红点打卡攻略)

[L2-037 包装机](#L2-037 包装机)

[L2-038 病毒溯源](#L2-038 病毒溯源)

[L2-039 清点代码库](#L2-039 清点代码库)

[L2-040 哲哲打游戏](#L2-040 哲哲打游戏)

[L2-041 插松枝](#L2-041 插松枝)

[L2-042 老板的作息表](#L2-042 老板的作息表)

[L2-043 龙龙送外卖](#L2-043 龙龙送外卖)

[L2-044 大众情人](#L2-044 大众情人)

L2部分的题目相较于L1会有所增难，L2比较偏向于考察数据结构的理解和应用，可以作为这方面的习题练手，提高代码熟练度。

L2-001 城市间紧急救援

分数 35

全屏浏览

切换布局

作者陈越

单位浙江大学

作为一个城市的应急救援队伍的负责人，你有一张特殊的全国地图。在地图上显示有多个分散的城市和一些连接城市的快速道路。每个城市的救援队数量和每一条连接两个城市的快速道路长度都标在地图上。当其他城市有紧急求助电话给你的时候，你的任务是带领你的救援队尽快赶往事发地，同时，一路上召集尽可能多的救援队。

输入格式:

输入第一行给出4个正整数N、M、S、D，其中N（2≤N≤500）是城市的个数，顺便假设城市的编号为0 ~ (N−1)；M是快速道路的条数；S是出发地的城市编号；D是目的地的城市编号。

第二行给出N个正整数，其中第i个数是第i个城市的救援队的数目，数字间以空格分隔。随后的M行中，每行给出一条快速道路的信息，分别是：城市1、城市2、快速道路的长度，中间用空格分开，数字均为整数且不超过500。输入保证救援可行且最优解唯一。

输出格式:

第一行输出最短路径的条数和能够召集的最多的救援队数量。第二行输出从S到D的路径中经过的城市编号。数字间以空格分隔，输出结尾不能有多余空格。

输入样例:

4 5 0 3
20 30 40 10
0 1 1
1 3 2
0 3 3
0 2 2
2 3 2

输出样例:

2 60
0 1 3

#include<iostream>
using namespace std;

int n, m, s, d;
int jiuyuandui[501];
int dist[501];
int graph[501][501];
int jiuyuandui2[501];
int parent[501];
int num[501];
int find1[501];

void dijkstra() {
    for(int i = 0; i < n; i++) {
        dist[i] = 99999;
        find1[i] = 0;
        num[i] = 0;
        jiuyuandui2[i] = 0;
    }
    dist[s] = 0;
    num[s] = 1;
    jiuyuandui2[s] = jiuyuandui[s];

    for(int i = 0; i < n - 1; i++) {
        int t = -1;
        for(int j = 0; j < n; j++) {
            if(find1[j] == 0 && (t == -1 || dist[t] > dist[j])) {
                t = j;
            }
        }
        for(int j = 0; j < n; j++) {
            if(dist[t] + graph[t][j] < dist[j]) {
                dist[j] = dist[t] + graph[t][j];
                num[j] = num[t];
                jiuyuandui2[j] = jiuyuandui2[t] + jiuyuandui[j];
                parent[j] = t;
            } else if(dist[t] + graph[t][j] == dist[j]) {
                num[j] += num[t];
                if(jiuyuandui2[t] + jiuyuandui[j] > jiuyuandui2[j]) {
                    jiuyuandui2[j] = jiuyuandui2[t] + jiuyuandui[j];
                    parent[j] = t;
                }
            }
        }
        find1[t] = 1;
    }
}

void print(int s, int t) {
    if(s == t) {
        cout << s << " ";
        return;
    }
    print(s, parent[t]);
    cout << t << " ";
}

int main() {
    cin >> n >> m >> s >> d;
    for(int i = 0; i < n; i++)  cin >> jiuyuandui[i];

    for(int i = 0; i < n; i++) {
        for(int j = 0; j < n; j++) {
            graph[i][j] = 999999;
        }
    }

    int aa, bb, cc;
    for(int i = 0; i < m; i++) {
        cin >> aa >> bb >> cc;
        graph[aa][bb] = graph[bb][aa] = cc;
    }

    dijkstra();
    cout << num[d] << " " << jiuyuandui2[d] << endl;

    print(s, parent[d]);
    cout << d << endl;

    return 0;
}

L2-002 链表去重

分数 25

全屏浏览

切换布局

作者陈越

单位浙江大学

给定一个带整数键值的链表 L，你需要把其中绝对值重复的键值结点删掉。即对每个键值 K，只有第一个绝对值等于 K 的结点被保留。同时，所有被删除的结点须被保存在另一个链表上。例如给定 L 为 21→-15→-15→-7→15，你需要输出去重后的链表 21→-15→-7，还有被删除的链表 -15→15。

输入格式：

输入在第一行给出 L 的第一个结点的地址和一个正整数 N（≤105，为结点总数）。一个结点的地址是非负的 5 位整数，空地址 NULL 用 -1 来表示。

随后 N 行，每行按以下格式描述一个结点：

地址 键值 下一个结点

其中地址是该结点的地址，键值是绝对值不超过104的整数，下一个结点是下个结点的地址。

输出格式：

首先输出去重后的链表，然后输出被删除的链表。每个结点占一行，按输入的格式输出。

输入样例：

00100 5
99999 -7 87654
23854 -15 00000
87654 15 -1
00000 -15 99999
00100 21 23854

输出样例：

00100 21 23854
23854 -15 99999
99999 -7 -1
00000 -15 87654
87654 15 -1

#include<iostream>
#include<vector>
#include<cmath>
using namespace std;
const int N=1e5+1;
struct node{
    int addres;
    int value;
    int next;
};

struct node G[N];//按照地址来储存结点
int visit[N];//用来记录该键值是否被访问过
vector<struct node> aa;
vector<struct node> bb;
int main(){
    int first;
    int n;
    cin>>first>>n;
    for(int i=0;i<n;i++){
        int add,value,next;
        cin>>add>>value>>next;
        G[add].addres=add;
        G[add].value=value;
        G[add].next=next;
    }
    int i=first;
    while(i!=-1){
        if(visit[abs(G[i].value)]==0){
            visit[abs(G[i].value)]=1;
            aa.push_back(G[i]);
        }
        else{
            bb.push_back(G[i]);
        }
        i=G[i].next;
    }
    for(int i=0;i<aa.size();i++){
        if(i==aa.size()-1){
            printf("%05d %d -1\n",aa[i].addres,aa[i].value);
        }
        else
        printf("%05d %d %05d\n",aa[i].addres,aa[i].value,aa[i+1].addres);
    }
     for(int i=0;i<bb.size();i++){
         if(i==bb.size()-1){
            printf("%05d %d -1\n",bb[i].addres,bb[i].value);
        }
        else
        printf("%05d %d %05d\n",bb[i].addres,bb[i].value,bb[i+1].addres);
    }
}

L2-003 月饼

分数 35

全屏浏览

切换布局

作者陈越

单位浙江大学

月饼是中国人在中秋佳节时吃的一种传统食品，不同地区有许多不同风味的月饼。现给定所有种类月饼的库存量、总售价、以及市场的最大需求量，请你计算可以获得的最大收益是多少。

注意：销售时允许取出一部分库存。样例给出的情形是这样的：假如我们有 3 种月饼，其库存量分别为 18、15、10 万吨，总售价分别为 75、72、45 亿元。如果市场的最大需求量只有 20 万吨，那么我们最大收益策略应该是卖出全部 15 万吨第 2 种月饼、以及 5 万吨第 3 种月饼，获得 72 + 45/2 = 94.5（亿元）。

输入格式：

每个输入包含一个测试用例。每个测试用例先给出一个不超过 1000 的正整数 N 表示月饼的种类数、以及不超过 500（以万吨为单位）的正整数 D 表示市场最大需求量。随后一行给出 N 个正数表示每种月饼的库存量（以万吨为单位）；最后一行给出 N 个正数表示每种月饼的总售价（以亿元为单位）。数字间以空格分隔。

输出格式：

对每组测试用例，在一行中输出最大收益，以亿元为单位并精确到小数点后 2 位。

输入样例：

3 20
18 15 10
75 72 45

输出样例：

94.50

#include<stdio.h>
struct yuebin{
    float kucun;
    float zong;
    float dan;
};
int main(){
    int n;
    int sum;
    scanf("%d %d",&n,&sum);
    struct yuebin y[1000];
    for(int i=0;i<2;i++){
        for(int j=0;j<n;j++){
            if(i==0){
                scanf("%f",&y[j].kucun);
            }
            else
                scanf("%f",&y[j].zong);
        }
    }
    for(int i=0;i<n;i++){
        y[i].dan=y[i].zong/y[i].kucun;
    }
    for(int i=0;i<n-1;i++){
        for(int j=0;j<n-i-1;j++){
            if(y[j].dan<y[j+1].dan){
                struct yuebin t=y[j];
                y[j]=y[j+1];
                y[j+1]=t;
            }
        }
    }
    float sumqian=0;
    for(int i=0;i<n;i++){
        if(sum<=y[i].kucun){
            sumqian=sumqian+sum*y[i].dan;
            break;
        }
        else{
            sumqian=sumqian+y[i].kucun*y[i].dan;
            sum=sum-y[i].kucun;
        }
    }
    printf("%.2f",sumqian);
}

L2-004 这是二叉搜索树吗？

分数 40

全屏浏览

切换布局

作者陈越

单位浙江大学

一棵二叉搜索树可被递归地定义为具有下列性质的二叉树：对于任一结点，

其左子树中所有结点的键值小于该结点的键值；
其右子树中所有结点的键值大于等于该结点的键值；
其左右子树都是二叉搜索树。

所谓二叉搜索树的"镜像"，即将所有结点的左右子树对换位置后所得到的树。

给定一个整数键值序列，现请你编写程序，判断这是否是对一棵二叉搜索树或其镜像进行前序遍历的结果。

输入格式：

输入的第一行给出正整数 N（≤1000）。随后一行给出 N 个整数键值，其间以空格分隔。

输出格式：

如果输入序列是对一棵二叉搜索树或其镜像进行前序遍历的结果，则首先在一行中输出 YES ，然后在下一行输出该树后序遍历的结果。数字间有 1 个空格，一行的首尾不得有多余空格。若答案是否，则输出 NO。

输入样例 1：

7
8 6 5 7 10 8 11

输出样例 1：

YES
5 7 6 8 11 10 8

输入样例 2：

7
8 10 11 8 6 7 5

输出样例 2：

YES
11 8 10 7 5 6 8

输入样例 3：

7
8 6 8 5 10 9 11

输出样例 3：

NO

#include<iostream>
#include<vector>
using namespace std;

vector<int> v;
int flag=0;
int pre[1000];
void find(int l,int r){
    if(l>r)
        return ;
    int tl=l+1;
    int tr=r;
    if(flag==0){
        while(tl<=r&&pre[tl]<pre[l])
          tl++;
        while(tr>l&&pre[tr]>=pre[l])
          tr--;
    }
   else{
       while(tl<=r&&pre[tl]>=pre[l])
          tl++;
        while(tr>l&&pre[tr]<pre[l])
          tr--;
   }
    if(tl-tr!=1)
        return ;
    find(l+1,tr);
    find(tl,r);
    v.push_back(pre[l]);
}
int main(){
    int n;
    cin>>n;
    for(int i=0;i<n;i++){
        cin>>pre[i];
    }
    find(0,n-1);
    if(v.size()==n){
        cout<<"YES"<<endl;
        for(int i=0;i<v.size();i++){
            if(i==0)
                cout<<v[i];
            else
                cout<<" "<<v[i];
        }
    }
    else{
        flag=1;
        v.clear();
        find(0,n-1);
        if(v.size()==n){
            cout<<"YES"<<endl;
        for(int i=0;i<v.size();i++){
            if(i==0)
                cout<<v[i];
            else
                cout<<" "<<v[i];
        }
        }
        else{
            cout<<"NO";
        }
    }
}

L2-005 集合相似度

分数 35

全屏浏览

切换布局

作者陈越

单位浙江大学

给定两个整数集合，它们的相似度定义为：Nc/Nt×100%。其中Nc是两个集合都有的不相等整数的个数，Nt是两个集合一共有的不相等整数的个数。你的任务就是计算任意一对给定集合的相似度。

输入格式：

输入第一行给出一个正整数N（≤50），是集合的个数。随后N行，每行对应一个集合。每个集合首先给出一个正整数M（≤104），是集合中元素的个数；然后跟M个[0,109]区间内的整数。

之后一行给出一个正整数K（≤2000），随后K行，每行对应一对需要计算相似度的集合的编号（集合从1到N编号）。数字间以空格分隔。

输出格式：

对每一对需要计算的集合，在一行中输出它们的相似度，为保留小数点后2位的百分比数字。

输入样例：

3
3 99 87 101
4 87 101 5 87
7 99 101 18 5 135 18 99
2
1 2
1 3

输出样例：

50.00%
33.33%

#include <iostream>
#include <set>
using namespace std;
int main() {
    int n;
    set<int> jihe[51];
    cin >> n;
    int k = 1;
    for(int i=0;i<n;i++){
        int m;
        cin>>m;
        for(int j=0;j<m;j++){
            int t;
            cin>>t;
            jihe[k].insert(t);
        }
        k++;
    }
    int c;
    int count = 0;
    cin >> c;
    while (c--) {
        int a, b;
        cin >> a >> b;
        int d = jihe[a].size() + jihe[b].size();
        for (auto it : jihe[a]) {
            if (jihe[b].find(it) != jihe[b].end()) {
                count++;
            }
        }
        double p = count * 100.0 / (d - count);
        printf("%.2f%%\n", p);
        count = 0;
    }
    return 0;
}

L2-006 树的遍历

分数 35

全屏浏览

切换布局

作者陈越

单位浙江大学

给定一棵二叉树的后序遍历和中序遍历，请你输出其层序遍历的序列。这里假设键值都是互不相等的正整数。

输入格式：

输入第一行给出一个正整数N（≤30），是二叉树中结点的个数。第二行给出其后序遍历序列。第三行给出其中序遍历序列。数字间以空格分隔。

输出格式：

在一行中输出该树的层序遍历的序列。数字间以1个空格分隔，行首尾不得有多余空格。

输入样例：

7
2 3 1 5 7 6 4
1 2 3 4 5 6 7

输出样例：

4 1 6 3 5 7 2

#include<iostream>
#include<vector>
using namespace std;
int N;
int hou[40];//后序遍历
int in[40];//中序遍历
vector<int> v(1e5,-1);//用来储存层序遍历

void build(int root,int start,int end,int index){
    if(start>end)
        return;
    int i=start;
    while(i<end&&in[i]!=hou[root])
        i++;
    v[index]=hou[root];
    build(root-end+i-1,start,i-1,index*2);
    build(root-1,i+1,end,index*2+1);
}
int main(){
    cin>>N;
    for(int i=1;i<=N;i++){
        cin>>hou[i];
    }
    for(int i=1;i<=N;i++){
        cin>>in[i];
    }
    build(N,1,N,1);
    int count=0;
    for(int i=1;i<v.size();i++){
        if(v[i]!=-1){
            count++;
            if(count==N){
                cout<<v[i];
            }
            else{
                cout<<v[i]<<" ";
            }
        }
    }
}

L2-007 家庭房产

分数 35

全屏浏览

切换布局

作者陈越

单位浙江大学

给定每个人的家庭成员和其自己名下的房产，请你统计出每个家庭的人口数、人均房产面积及房产套数。

输入格式：

输入第一行给出一个正整数N（≤1000），随后N行，每行按下列格式给出一个人的房产：

编号 父 母 k 孩子1 ... 孩子k 房产套数 总面积

其中编号是每个人独有的一个4位数的编号；父和母分别是该编号对应的这个人的父母的编号（如果已经过世，则显示-1）；k（0≤k≤5）是该人的子女的个数；孩子i是其子女的编号。

输出格式：

首先在第一行输出家庭个数（所有有亲属关系的人都属于同一个家庭）。随后按下列格式输出每个家庭的信息：

家庭成员的最小编号 家庭人口数 人均房产套数 人均房产面积

其中人均值要求保留小数点后3位。家庭信息首先按人均面积降序输出，若有并列，则按成员编号的升序输出。

输入样例：

10
6666 5551 5552 1 7777 1 100
1234 5678 9012 1 0002 2 300
8888 -1 -1 0 1 1000
2468 0001 0004 1 2222 1 500
7777 6666 -1 0 2 300
3721 -1 -1 1 2333 2 150
9012 -1 -1 3 1236 1235 1234 1 100
1235 5678 9012 0 1 50
2222 1236 2468 2 6661 6662 1 300
2333 -1 3721 3 6661 6662 6663 1 100

输出样例：

3
8888 1 1.000 1000.000
0001 15 0.600 100.000
5551 4 0.750 100.000

#include<stdio.h>
#include<stdlib.h>

// 定义家庭成员结构体
typedef struct {
	int master;   // 本人编号
	int fa;       // 父亲编号
	int mu;       // 母亲编号
	int kidn;     // 孩子数量
	int kids[10]; // 孩子编号数组
	double sum;   // 收入总和
	double area;  // 房产总面积
} node;

node a[10005];   // 存储家庭成员信息

// 定义家庭汇总信息结构体
typedef struct {
	int people;   // 家庭成员数量
	int id;       // 家庭编号
	double sum;   // 平均收入
	double area;  // 平均房产面积
    int flag;
} node1;

node1 b[10005];  // 存储家庭汇总信息

// 定义家庭排序信息结构体
typedef struct {
	int people;   // 家庭成员数量
	int id;       // 家庭编号
	double sum;   // 平均收入
	double area;  // 平均房产面积
} node2;

node2 c[1005];   // 存储家庭排序信息

int n;            // 家庭数量
int cnt=0;        // 计数器
int visit[10005]={0};  // 访问标记数组
int home[10005];  // 并查集数组

// 查找根节点
int find(int x){
	if(x==home[x])
       return x;
    else
       return find(home[x]);
}

// 合并集合
void un(int a,int b){
	int f1=find(a);
	int f2=find(b);
	if(f1>f2){
		home[f1]=f2;
	}else{
		home[f2]=f1;
	}
}

int main()
{
	for(int i=0;i<10005;i++){   // 初始化并查集
		home[i]=i;
		b[i].people = 0;    // 初始家庭成员数量为0
		b[i].id = i;        // 家庭编号为本人编号
		b[i].sum = 0.0;     // 初始收入总和为0
		b[i].area = 0.0;    // 初始房产总面积为0
		b[i].flag=0;        // 该题所需，并非并查集的要求
	}
	scanf("%d",&n);  // 输入家庭数量
	for(int i=0;i<n;i++){
		scanf("%d %d %d %d",&a[i].master,&a[i].fa,&a[i].mu,&a[i].kidn);  // 输入家庭成员信息
		visit[a[i].master]=1;  // 标记已访问
		if(a[i].fa!=-1){
			un(a[i].master,a[i].fa);  // 合并父亲
			visit[a[i].fa]=1;  // 标记已访问
		}
		if(a[i].mu!=-1){
			un(a[i].master,a[i].mu);  // 合并母亲
			visit[a[i].mu]=1;  // 标记已访问
		}
		for(int j=0;j<a[i].kidn;j++){
			scanf("%d",&a[i].kids[j]);
			un(a[i].master,a[i].kids[j]);  // 合并孩子
			visit[a[i].kids[j]]=1;  // 标记已访问
		}
		scanf("%lf %lf",&a[i].sum,&a[i].area);  // 输入收入总和和房产总面积
	}
	// 统计每个家庭的收入总和和房产总面积
	for(int i=0;i<n;i++){
		int id=find(a[i].master);  // 获取家庭根节点
		b[id].id=id;
		b[id].sum+=a[i].sum;  // 更新收入总和
		b[id].area+=a[i].area;  // 更新房产总面积
		b[id].flag=1;  // 标记家庭根节点已访问
	}
	// 统计每个家庭的成员数量
	for(int i=0;i<10005;i++){
		if(visit!=0){
			b[find(i)].people+=1;  // 统计家庭成员数量
		}
	}
	// 计算每个家庭的平均收入和平均房产面积
	for(int i=0;i<10005;i++){
		if(b[i].flag){
			b[i].sum=b[i].sum/b[i].people;  // 计算平均收入
			b[i].area=b[i].area/b[i].people;  // 计算平均房产面积
		}
	}
	// 将有效的家庭汇总信息存入排序数组
	for(int i=0;i<10005;i++){
		if(b[i].flag){
			c[cnt].id=b[i].id;
			c[cnt].area=b[i].area;
			c[cnt].people=b[i].people;
			c[cnt].sum=b[i].sum;
			cnt++;	
		}
	}
	// 对家庭排序数组进行排序
	node2 t;
	for(int i=0;i<n;i++){
		for(int j=i+1;j<n;j++){
			if(c[i].area<c[j].area){
				t=c[i];
				c[i]=c[j];
				c[j]=t;
			}else{
				if(c[i].area==c[j].area){
					if(c[j].id<c[i].id){
						t=c[i];
						c[i]=c[j];
						c[j]=t;
					}
				}
			}
		}
	}
	// 输出家庭汇总信息
	printf("%d\n",cnt);
	for(int i=0;i<cnt;i++){
		printf("%04d %d %.3lf %.3lf\n",c[i].id,c[i].people,c[i].sum,c[i].area);
	}
	return 0;
}

L2-008 最长对称子串

分数 40

全屏浏览

切换布局

作者陈越

单位浙江大学

对给定的字符串，本题要求你输出最长对称子串的长度。例如，给定Is PAT&TAP symmetric?，最长对称子串为s PAT&TAP s，于是你应该输出11。

输入格式：

输入在一行中给出长度不超过1000的非空字符串。

输出格式：

在一行中输出最长对称子串的长度。

输入样例：

Is PAT&TAP symmetric?

输出样例：

11

#include<iostream>
#include<string>
using namespace std;
int main(){
    string s;
    getline(cin,s);
    int sum=1;
    int max=-1;
    if(s.length()==1){
        cout<<1;
        return 0;
    }
    for(int i=1;i<s.length()-1;i++){
        int p=i-1;
        int q=i+1;
        sum=1;
        while(s[p]==s[q]&&p>=0&&q<s.length()){
            p--;
            q++;
            sum+=2;
        }
        if(max<sum)
            max=sum;
    }
    int sum1=0;
    for(int i=0;i<s.length()-1;i++){
        int p=i;
        int q=i+1;
        sum1=0;
        while(s[p]==s[q]&&p>=0&&q<s.length()){
            p--;
            q++;
            sum1=sum1+2;
        }
        if(max<sum1)
            max=sum1;
    }
    cout<<max;
}

L2-009 抢红包

分数 35

全屏浏览

切换布局

作者陈越

单位浙江大学

没有人没抢过红包吧...... 这里给出N个人之间互相发红包、抢红包的记录，请你统计一下他们抢红包的收获。

输入格式：

输入第一行给出一个正整数N（≤104），即参与发红包和抢红包的总人数，则这些人从1到N编号。随后N行，第i行给出编号为i的人发红包的记录，格式如下：

KN1P1⋯NKPK

其中K（0≤K≤20）是发出去的红包个数，Ni是抢到红包的人的编号，Pi（>0）是其抢到的红包金额（以分为单位）。注意：对于同一个人发出的红包，每人最多只能抢1次，不能重复抢。

输出格式：

按照收入金额从高到低的递减顺序输出每个人的编号和收入金额（以元为单位，输出小数点后2位）。每个人的信息占一行，两数字间有1个空格。如果收入金额有并列，则按抢到红包的个数递减输出；如果还有并列，则按个人编号递增输出。

输入样例：

10
3 2 22 10 58 8 125
5 1 345 3 211 5 233 7 13 8 101
1 7 8800
2 1 1000 2 1000
2 4 250 10 320
6 5 11 9 22 8 33 7 44 10 55 4 2
1 3 8800
2 1 23 2 123
1 8 250
4 2 121 4 516 7 112 9 10

输出样例：

1 11.63
2 3.63
8 3.63
3 2.11
7 1.69
6 -1.67
9 -2.18
10 -3.26
5 -3.26
4 -12.32

#include<iostream>
using namespace std;
struct person {
    int id;
    int cnt;//抢到红包个数
    int price;
};
int main() {
    int n, k;
    cin >> n;
    person p[n + 1];
    for (int i = 1; i <= n; i++) {
        p[i].cnt = 0;
        p[i].price = 0;
    }
    for (int i = 1; i <= n; i++) {
        p[i].id = i;
        cin >> k;
        for (int j = 1; j <= k; j++) {
            int a;
            int b;
            cin >> a >> b;
            p[i].price -= b;
            p[a].price += b;
            p[a].cnt++;
        }
    }
    for(int i=1;i<n;i++){
        int max=i;
        for(int j=i+1;j<n+1;j++){
            if(p[max].price<p[j].price)
                max=j;
            else if(p[max].price==p[j].price){
                if(p[max].cnt<p[j].cnt)
                    max=j;
                else if(p[max].cnt==p[j].cnt){
                    if(p[max].id>p[j].id)
                        max=j;
                }
            }
        }
        struct person t;
        t=p[max];
        p[max]=p[i];
        p[i]=t;
    }
	for (int i = 1; i <= n; i++) {
		printf("%d %.2lf\n", p[i].id,  1.0 * p[i].price / 100);
	}
	return 0;
}

L2-010 排座位

分数 35

全屏浏览

切换布局

作者陈越

单位浙江大学

布置宴席最微妙的事情，就是给前来参宴的各位宾客安排座位。无论如何，总不能把两个死对头排到同一张宴会桌旁！这个艰巨任务现在就交给你，对任何一对客人，请编写程序告诉主人他们是否能被安排同席。

输入格式：

输入第一行给出3个正整数：N（≤100），即前来参宴的宾客总人数，则这些人从1到N编号；M为已知两两宾客之间的关系数；K为查询的条数。随后M行，每行给出一对宾客之间的关系，格式为：宾客1 宾客2 关系，其中关系为1表示是朋友，-1表示是死对头。注意两个人不可能既是朋友又是敌人。最后K行，每行给出一对需要查询的宾客编号。

这里假设朋友的朋友也是朋友。但敌人的敌人并不一定就是朋友，朋友的敌人也不一定是敌人。只有单纯直接的敌对关系才是绝对不能同席的。

输出格式：

对每个查询输出一行结果：如果两位宾客之间是朋友，且没有敌对关系，则输出No problem；如果他们之间并不是朋友，但也不敌对，则输出OK；如果他们之间有敌对，然而也有共同的朋友，则输出OK but...；如果他们之间只有敌对关系，则输出No way。

输入样例：

输出样例：

No problem
OK
OK but...
No way

#include<stdio.h>
int guanxi[101][101]={0};
int friend[101];
void init(int n){
    for(int i=0;i<n;i++){
        friend[i]=i;
    }
}
int find(int x){
    if(x==friend[x])
        return x;
    else
        return find(friend[x]);
}
void union1(int a,int b){
    int f1=find(a);
    int f2=find(b);
    if(f1>f2)
        friend[f1]=f2;
    else
        friend[f2]=f1;
}
int main(){
    int n,m,k;
    scanf("%d %d %d",&n,&m,&k);
    init(n);
    for(int i=0;i<m;i++){
        int x,y,z;
        scanf("%d %d %d",&x,&y,&z);
        if(z==1)
            union1(x,y);
        else{
            guanxi[x][y]=1;
            guanxi[y][x]=1;
            //这里的1表示他们敌对
        }
    }
    for(int i=0;i<k;i++){
        int a1,a2;
        scanf("%d %d",&a1,&a2);
        int x=find(a1);
        int y=find(a2);
        if(x==y&&guanxi[a1][a2]==0)
            printf("No problem\n");
        else if(x!=y&&guanxi[a1][a2]==0)
            printf("OK\n");
        else if(x==y&&guanxi[a1][a2]==1)
            printf("OK but...\n");
        else if(x!=y&&guanxi[a1][a2]==1)
            printf("No way\n");
    }
}

L2-011 玩转二叉树

分数 35

全屏浏览

切换布局

作者陈越

单位浙江大学

给定一棵二叉树的中序遍历和前序遍历，请你先将树做个镜面反转，再输出反转后的层序遍历的序列。所谓镜面反转，是指将所有非叶结点的左右孩子对换。这里假设键值都是互不相等的正整数。

输入格式：

输入第一行给出一个正整数N（≤30），是二叉树中结点的个数。第二行给出其中序遍历序列。第三行给出其前序遍历序列。数字间以空格分隔。

输出格式：

在一行中输出该树反转后的层序遍历的序列。数字间以1个空格分隔，行首尾不得有多余空格。

输入样例：

7
1 2 3 4 5 6 7
4 1 3 2 6 5 7

输出样例：

4 6 1 7 5 3 2

#include<stdio.h>
#include<stdlib.h>
struct treenode{
    int data;
    struct treenode*left;
    struct treenode* right;
};
typedef struct treenode* tree;
int in[30];
int pre[30];

tree bulid(int in[],int pre[],int n){
    tree t;
    if(n==0)
        return NULL;
    else{
        t=(tree)malloc(sizeof(struct treenode));
        t->data=pre[0];
        t->left=NULL;
        t->right=NULL;
        int i;
        for(i=0;i<n;i++){
            if(in[i]==pre[0])
                break;
        }
        t->left=bulid(in,pre+1,i);
        t->right=bulid(in+i+1,pre+i+1,n-i-1);
        return t;
    }
}

tree fanzhuan(tree t){
    tree k;
    if(t!=NULL){
        if(t->left!=NULL||t->right!=NULL){
            k=t->left;
            t->left=t->right;
            t->right=k;
        }
        fanzhuan(t->left);
        fanzhuan(t->right);
    }
    return t;
}

void cengxu(tree BT,int n){
     if(!BT)
        return;
    int len=1;
    int pos;
    int sum=0;
    tree a[101],b[101];
    a[0]=BT;
    while(1){
        if(len==0)
            return;
        pos=0;
        for(int i=0;i<len;i++){
            if(a[i]->left!=NULL)//如果它的左节点不为空，就存到b数组里
                b[pos++]=a[i]->left;
            if(a[i]->right!=NULL)//如果它的右节点不为空，就存到b数组里
                b[pos++]=a[i]->right;
            if(a[i]!=NULL){//不为空输出
                printf("%d",a[i]->data);
                sum++;
            }
            if(sum!=n)
                printf(" ");
        }
        len=pos;//为下一次循环做准备
        //更新数组走下一次层序
        for(int i=0;i<len;i++)
            a[i]=b[i];
    }
}

int main(){
    tree shu;
    int n;
    scanf("%d",&n);
    for(int i=0;i<n;i++){
        scanf("%d",&in[i]);
    }
    for(int i=0;i<n;i++){
        scanf("%d",&pre[i]);
    }
    shu=bulid(in,pre,n);
    shu=fanzhuan(shu);
    cengxu(shu,n);
}

L2-012 关于堆的判断

分数 30

全屏浏览

切换布局

作者陈越

单位浙江大学

将一系列给定数字顺序插入一个初始为空的最小堆。随后判断一系列相关命题是否为真。命题分下列几种：

x is the root：x是根结点；
x and y are siblings：x和y是兄弟结点；
x is the parent of y：x是y的父结点；
x is a child of y：x是y的一个子结点。

输入格式：

每组测试第 1 行包含 2 个正整数 n（≤ 1000）和 m（≤ 20），分别是插入元素的个数、以及需要判断的命题数。下一行给出区间 [−10000,10000] 内的 n 个要被插入一个初始为空的最小堆的整数。之后 m 行，每行给出一个命题。题目保证命题中的结点键值都是存在的。

输出格式：

对输入的每个命题，如果其为真，则在一行中输出 T，否则输出 F。

输入样例：

5 4
46 23 26 24 10
24 is the root
26 and 23 are siblings
46 is the parent of 23
23 is a child of 10

输出样例：

F
T
F
T

#include<stdio.h>
void swap(int a[],int i,int k){
    int t=a[i];
    a[i]=a[k];
    a[k]=t;
}
void stack(int a[],int s){
    for(int i=s/2;i>0;s=i,i/=2)
        if(a[s]<a[i])
            swap(a,s,i);
}
int find(int a[],int n,int m){
    for(int l=1;l<=n;l++)
        if(a[l]==m) return l;
    return 0;
}
int main(){
    int n,m,i,p,q;
    scanf("%d %d",&n,&m);
    int a[n+1];
    for(i=1;i<=n;i++){
        scanf("%d",&a[i]);
        stack(a,i);
    }getchar();
    while(m--){
        char g[10],h[10],str[10];
        scanf("%d %s %s %s",&p,g,h,str);
        if(str[0]=='r'){
            if(a[1]!=p) printf("F\n");
            else printf("T\n");
        }else if(str[0]=='a'){
            scanf("%s",g);
            sscanf(h,"%d",&q);
            if(find(a,n,p)/2==find(a,n,q)/2)
                printf("T\n");
            else printf("F\n");
        }else if(str[0]=='p'){
            scanf("%s %d",g,&q);
            if(find(a,n,p)==find(a,n,q)/2)
                printf("T\n");
            else printf("F\n");
        }else if(str[0]=='c'){
            scanf("%s %d",g,&q);
            if(find(a,n,p)/2==find(a,n,q))
                printf("T\n");
            else printf("F\n");
        }
    }
    return 0;
}

L2-013 红色警报

分数 35

全屏浏览

切换布局

作者陈越

单位浙江大学

战争中保持各个城市间的连通性非常重要。本题要求你编写一个报警程序，当失去一个城市导致国家被分裂为多个无法连通的区域时，就发出红色警报。注意：若该国本来就不完全连通，是分裂的k个区域，而失去一个城市并不改变其他城市之间的连通性，则不要发出警报。

输入格式：

输入在第一行给出两个整数N（0 < N ≤ 500）和M（≤ 5000），分别为城市个数（于是默认城市从0到N-1编号）和连接两城市的通路条数。随后M行，每行给出一条通路所连接的两个城市的编号，其间以1个空格分隔。在城市信息之后给出被攻占的信息，即一个正整数K和随后的K个被攻占的城市的编号。

注意：输入保证给出的被攻占的城市编号都是合法的且无重复，但并不保证给出的通路没有重复。

输出格式：

对每个被攻占的城市，如果它会改变整个国家的连通性，则输出Red Alert: City k is lost!，其中k是该城市的编号；否则只输出City k is lost.即可。如果该国失去了最后一个城市，则增加一行输出Game Over.。

输入样例：

输出样例：

City 1 is lost.
City 2 is lost.
Red Alert: City 0 is lost!
City 4 is lost.
City 3 is lost.
Game Over.

#include<stdio.h>
int a[505];
struct edge{
    int a1;
    int a2;
};
int find(int x){
    if(x!=a[x])
        return find(a[x]);
    else
        return x;
}
void un(int x,int y){
    int f1=find(x);
    int f2=find(y);
    if(f1>f2)
        a[f1]=f2;
    else
        a[f2]=f1;
}
void init(int n){
    for(int i=0;i<n;i++){
        a[i]=i;
    }
}
int main(){
    int n,m;
    int u,v;
    int visit[505]={0};
    struct edge e[5005];
    int cnt=0;
    int sum=0;//城市区块
    scanf("%d %d",&n,&m);
    init(n);
    for(int i=0;i<m;i++){
        scanf("%d %d",&u,&v);
        e[i].a1=u;
        e[i].a2=v;
        un(u,v);
    }
    for(int i=0;i<n;i++){
        if(a[i]==i)
            sum++;
    }
    int k;
    scanf("%d",&k);
    for(int i=0;i<k;i++){
        cnt=0;
        init(n);
        int num;
        scanf("%d",&num);
        visit[num]=1;
        for(int j=0;j<m;j++){
            if(visit[e[j].a1]==1||visit[e[j].a2]==1)
                continue;
            else
                un(e[j].a1,e[j].a2);
        }
        for(int j=0;j<n;j++){
            if(a[j]==j){
                cnt++;
            }
        }
        if(cnt-1==sum||cnt==sum)
            printf("City %d is lost.\n",num);
        else
            printf("Red Alert: City %d is lost!\n",num);
        sum=cnt;
    }
    if(k>=n)
        printf("Game Over.");
}

L2-014 列车调度

分数 35

全屏浏览

切换布局

作者陈越

单位浙江大学

火车站的列车调度铁轨的结构如下图所示。

两端分别是一条入口（Entrance）轨道和一条出口（Exit）轨道，它们之间有N条平行的轨道。每趟列车从入口可以选择任意一条轨道进入，最后从出口离开。在图中有9趟列车，在入口处按照{8，4，2，5，3，9，1，6，7}的顺序排队等待进入。如果要求它们必须按序号递减的顺序从出口离开，则至少需要多少条平行铁轨用于调度？

输入格式：

输入第一行给出一个整数N (2 ≤ N ≤105)，下一行给出从1到N的整数序号的一个重排列。数字间以空格分隔。

输出格式：

在一行中输出可以将输入的列车按序号递减的顺序调离所需要的最少的铁轨条数。

输入样例：

9
8 4 2 5 3 9 1 6 7

输出样例：

4

#include <stdio.h>
#include <stdlib.h>
int a[100005];
int main(){
    int n,i,b,j=0,flag=0;
    scanf("%d",&n);
    for(i=0;i<n;i++){
        scanf("%d",&b);
        if(j==0&&flag==0){
            a[j]=b;
            flag=1;
        }
        else{
            if(b>a[j]){
                j++;
                a[j]=b;
            }
            else{
                int k;
                for(k=0;k<=j;k++){
                    if(a[k]>b)
                        break;
                }
                a[k]=b;
            }
        }
    }
    printf("%d",j+1);
}

L2-015 互评成绩

分数 35

全屏浏览

切换布局

作者陈越

单位浙江大学

学生互评作业的简单规则是这样定的：每个人的作业会被k个同学评审，得到k个成绩。系统需要去掉一个最高分和一个最低分，将剩下的分数取平均，就得到这个学生的最后成绩。本题就要求你编写这个互评系统的算分模块。

输入格式：

输入第一行给出3个正整数N（3 < N ≤104，学生总数）、k（3 ≤ k ≤ 10，每份作业的评审数）、M（≤ 20，需要输出的学生数）。随后N行，每行给出一份作业得到的k个评审成绩（在区间[0, 100]内），其间以空格分隔。

输出格式：

按非递减顺序输出最后得分最高的M个成绩，保留小数点后3位。分数间有1个空格，行首尾不得有多余空格。

输入样例：

6 5 3
88 90 85 99 60
67 60 80 76 70
90 93 96 99 99
78 65 77 70 72
88 88 88 88 88
55 55 55 55 55

输出样例：

87.667 88.000 96.000

#include <stdio.h>
#include <stdlib.h>
int main() {
    int n, k, m;
    scanf("%d %d %d", &n, &k, &m);
    double a[30] = {0};
    double sum[10000] = {0}; // 注意数组大小

    for (int i = 0; i < n; i++) {
        for (int j = 0; j < k; j++) {
            scanf("%lf", &a[j]);
            sum[i] += a[j];
        }
        for (int j = 0; j < k - 1; j++) {
            for (int l = j + 1; l < k; l++) {
                if (a[j] > a[l]) {
                    double temp = a[j];
                    a[j] = a[l];
                    a[l] = temp;
                }
            }
        }
        sum[i] = sum[i] - a[0] - a[k - 1];
    }

    for (int i = 0; i < n - 1; i++) {
        for (int j = i + 1; j < n; j++) {
            if (sum[i] > sum[j]) {
                double temp = sum[i];
                sum[i] = sum[j];
                sum[j] = temp;
            }
        }
    }

    printf("%.3lf", sum[n - m] / (k - 2));
    for (int i = n - m + 1; i < n; i++) {
        printf(" %.3lf", sum[i] / (k - 2));
    }

    return 0;
}

L2-016 愿天下有情人都是失散多年的兄妹

分数 35

全屏浏览

切换布局

作者陈越

单位浙江大学

呵呵。大家都知道五服以内不得通婚，即两个人最近的共同祖先如果在五代以内（即本人、父母、祖父母、曾祖父母、高祖父母）则不可通婚。本题就请你帮助一对有情人判断一下，他们究竟是否可以成婚？

输入格式：

输入第一行给出一个正整数N（2 ≤ N ≤104），随后N行，每行按以下格式给出一个人的信息：

本人ID 性别 父亲ID 母亲ID

其中ID是5位数字，每人不同；性别M代表男性、F代表女性。如果某人的父亲或母亲已经不可考，则相应的ID位置上标记为-1。

接下来给出一个正整数K，随后K行，每行给出一对有情人的ID，其间以空格分隔。

注意：题目保证两个人是同辈，每人只有一个性别，并且血缘关系网中没有乱伦或隔辈成婚的情况。

输出格式：

对每一对有情人，判断他们的关系是否可以通婚：如果两人是同性，输出Never Mind；如果是异性并且关系出了五服，输出Yes；如果异性关系未出五服，输出No。

输入样例：

24
00001 M 01111 -1
00002 F 02222 03333
00003 M 02222 03333
00004 F 04444 03333
00005 M 04444 05555
00006 F 04444 05555
00007 F 06666 07777
00008 M 06666 07777
00009 M 00001 00002
00010 M 00003 00006
00011 F 00005 00007
00012 F 00008 08888
00013 F 00009 00011
00014 M 00010 09999
00015 M 00010 09999
00016 M 10000 00012
00017 F -1 00012
00018 F 11000 00013
00019 F 11100 00018
00020 F 00015 11110
00021 M 11100 00020
00022 M 00016 -1
00023 M 10012 00017
00024 M 00022 10013
9
00021 00024
00019 00024
00011 00012
00022 00018
00001 00004
00013 00016
00017 00015
00019 00021
00010 00011

输出样例：

Never Mind
Yes
Never Mind
No
Yes
No
Yes
No
No

#include <stdio.h>
#define N 100010
int n, fa[N], ma[N], done[N], flag, t, a, b, k;
char sex[N];
void check(int x, int deep) {
    if (done[x] == 1) 
        flag = 0;
    done[x] = 1;
    if (deep == 5) 
        return;
    if (fa[x] != -1) 
        check(fa[x], deep + 1);
    if (ma[x] != -1) 
        check(ma[x], deep + 1);
}

int main() {
    char ch;
    scanf("%d", &n);
    for (int i = 0; i < N; i++) {
        fa[i] = -1;
        ma[i] = -1;
    }
    for (int i = 0; i < n; i++) {
        scanf("%d", &t);
        getchar();
        scanf("%c", &ch);
        scanf("%d %d", &a, &b);
        sex[t] = ch, fa[t] = a, ma[t] = b;
        if (a != -1) 
            sex[a] = 'M';
        if (b != -1) 
            sex[b] = 'F';
    }
    scanf("%d", &k);
    for (int i = 0; i < k; i++) {
        scanf("%d %d", &a, &b);
        if (sex[a] == sex[b]) 
            printf("Never Mind\n");
        else {
            flag = 1;
            for (int j = 0; j < N; j++) {
                done[j] = 0;
            }
            check(a, 1);
            check(b, 1);
            if (flag) 
                printf("Yes\n");
            else 
                printf("No\n");
        }
    }
    return 0;
}

L2-017 人以群分

分数 35

全屏浏览

切换布局

作者陈越

单位浙江大学

社交网络中我们给每个人定义了一个"活跃度"，现希望根据这个指标把人群分为两大类，即外向型（outgoing，即活跃度高的）和内向型（introverted，即活跃度低的）。要求两类人群的规模尽可能接近，而他们的总活跃度差距尽可能拉开。

输入格式：

输入第一行给出一个正整数N（2≤N≤105）。随后一行给出N个正整数，分别是每个人的活跃度，其间以空格分隔。题目保证这些数字以及它们的和都不会超过231。

输出格式：

按下列格式输出：

Outgoing #: N1
Introverted #: N2
Diff = N3

其中N1是外向型人的个数；N2是内向型人的个数；N3是两群人总活跃度之差的绝对值。

输入样例1：

10
23 8 10 99 46 2333 46 1 666 555

输出样例1：

Outgoing #: 5
Introverted #: 5
Diff = 3611

输入样例2：

13
110 79 218 69 3721 100 29 135 2 6 13 5188 85

输出样例2：

Outgoing #: 7
Introverted #: 6
Diff = 9359

#include <iostream>
#include <algorithm>
using namespace std;
int main(){
    int num;
    int different=0;
    cin >> num;
    int people[num];
    for (int i = 0; i < num; i++){
        cin >> people[i];
        different += people[i];
    }
    sort(people, people + num);
    //这里用数学公式退一下就好了，其实也可以分开来无所谓
    //这道题的主要思想就是人数对半分，如果是偶数就对半分，如果是奇数，外向的人肯定要占多数才能实现最大化
    for (int i = 0; i < num / 2; i++)
        different-= 2 * people[i];
    cout << "Outgoing #: " << (num + 1) / 2 << endl;
    cout << "Introverted #: " << num / 2 << endl;
    cout << "Diff = " << different << endl;
    system("pause");
    return 0;
}

L2-018 多项式A除以B

分数 35

全屏浏览

切换布局

作者陈越

单位浙江大学

这仍然是一道关于A/B的题，只不过A和B都换成了多项式。你需要计算两个多项式相除的商Q和余R，其中R的阶数必须小于B的阶数。

输入格式：

输入分两行，每行给出一个非零多项式，先给出A，再给出B。每行的格式如下：

N e[1] c[1] ... e[N] c[N]

其中N是该多项式非零项的个数，e[i]是第i个非零项的指数，c[i]是第i个非零项的系数。各项按照指数递减的顺序给出，保证所有指数是各不相同的非负整数，所有系数是非零整数，所有整数在整型范围内。

输出格式：

分两行先后输出商和余，输出格式与输入格式相同，输出的系数保留小数点后1位。同行数字间以1个空格分隔，行首尾不得有多余空格。注意：零多项式是一个特殊多项式，对应输出为0 0 0.0。但非零多项式不能输出零系数（包括舍入后为0.0）的项。在样例中，余多项式其实有常数项-1/27，但因其舍入后为0.0，故不输出。

输入样例：

4 4 1 2 -3 1 -1 0 -1
3 2 3 1 -2 0 1

输出样例：

3 2 0.3 1 0.2 0 -1.0
1 1 -3.1

#include<stdio.h>
#include<math.h>
double a[100000],b[100000],c[100000];
int main(){
    int n;
    int m;
    int k;
    int t;
    int l;
    int ma;
    int mb;
    int numa=0,numb=0;
    scanf("%d",&n);
    for(int i=0;i<n;i++){
        scanf("%d",&m);
        scanf("%lf",&a[m]);
        if(i==0)
            ma=m;//最高次
    }
    scanf("%d",&l);
    for(int i=0;i<l;i++){
        scanf("%d",&m);
        scanf("%lf",&b[m]);
        if(i==0)
            mb=m;
    }
    for(int i=ma;i>=mb;i--){
        c[i-mb]=a[i]/b[mb];//次数相减就是系数相除
        for(int j=mb;j>=0;j--){
            a[i+j-mb]-=b[j]*c[i-mb];
        }
    }
    for(int i=ma-mb;i>=0;i--){
        if(fabs(c[i])>0.01){
            if(fabs(c[i])<0.05){
                c[i]=0;
            }
            else{
                numa++;
            }
        }
    }
    for(int i=mb-1;i>=0;i--){
        if(fabs(a[i])>pow(10,-2)){
            if(fabs(a[i])<0.05){
                a[i]=0;
            }
            else{
                numb++;
            }
        }
    }
    if(numa==0){
        printf("0 0 0.0\n");
    }
    else{
        printf("%d",numa);
        for(int i=ma-mb;i>=0;i--){
            if(fabs(c[i])>pow(10,-2)){
                printf(" %d %.1lf",i,c[i]);
            }
        }
        printf("\n");
    }
    if(numb==0){
        printf("0 0 0.0\n");
    }
    else{
        printf("%d",numb);
        for(int i=mb-1;i>=0;i--){
            if(fabs(a[i])>1e-6){
                printf(" %d %.1lf",i,a[i]);
            }
        }
        printf("\n");
    }
}

L2-019 悄悄关注

分数 35

全屏浏览

切换布局

作者陈越

单位浙江大学

新浪微博上有个"悄悄关注"，一个用户悄悄关注的人，不出现在这个用户的关注列表上，但系统会推送其悄悄关注的人发表的微博给该用户。现在我们来做一回网络侦探，根据某人的关注列表和其对其他用户的点赞情况，扒出有可能被其悄悄关注的人。

输入格式：

输入首先在第一行给出某用户的关注列表，格式如下：

人数N 用户1 用户2 ...... 用户N

其中N是不超过5000的正整数，每个用户i（i=1, ..., N）是被其关注的用户的ID，是长度为4位的由数字和英文字母组成的字符串，各项间以空格分隔。

之后给出该用户点赞的信息：首先给出一个不超过10000的正整数M，随后M行，每行给出一个被其点赞的用户ID和对该用户的点赞次数（不超过1000），以空格分隔。注意：用户ID是一个用户的唯一身份标识。题目保证在关注列表中没有重复用户，在点赞信息中也没有重复用户。

输出格式：

我们认为被该用户点赞次数大于其点赞平均数、且不在其关注列表上的人，很可能是其悄悄关注的人。根据这个假设，请你按用户ID字母序的升序输出可能是其悄悄关注的人，每行1个ID。如果其实并没有这样的人，则输出"Bing Mei You"。

输入样例1：

10 GAO3 Magi Zha1 Sen1 Quan FaMK LSum Eins FatM LLao
8
Magi 50
Pota 30
LLao 3
Ammy 48
Dave 15
GAO3 31
Zoro 1
Cath 60

输出样例1：

Ammy
Cath
Pota

输入样例2：

11 GAO3 Magi Zha1 Sen1 Quan FaMK LSum Eins FatM LLao Pota
7
Magi 50
Pota 30
LLao 48
Ammy 3
Dave 15
GAO3 31
Zoro 29

输出样例2：

Bing Mei You

#include<stdio.h>
#include<string.h>
#include<stdlib.h>
typedef struct user user;
struct user{
    char name[5];
    int dianzancishu;
};
int panduan(char names[5000][5],char* name,int n){
    for(int i=0;i<n;i++){
        int flag=strcmp(names[i],name);
        if(flag==0)
            return 1;  //表示在这个榜上
    }
    return 0;
}
int cmp(const void *a,const void *b)
{
     return strcmp((char*)a, (char*)b);
}
int main(){
    int n;
    scanf("%d",&n);
    char names[5000][5];
    user users[10000];
    for(int i=0;i<n;i++){
        scanf("%s",names[i]);
    }
    int m;
    int sum=0;
    scanf("%d",&m);
    for(int i=0;i<m;i++){
        scanf("%s %d",users[i].name,&users[i].dianzancishu);
        sum=sum+users[i].dianzancishu;
    }
    float summ=sum*1.0/m;
    //接下来判断其是否在关注列表上
    char namess[5000][5];
        int k=0;
    for(int i=0;i<m;i++){
        if(panduan(names,users[i].name,n)==0&&users[i].dianzancishu>summ){
            strcpy(namess[k++],users[i].name);
        }
    }
    if(k==0)
        printf("Bing Mei You");
    else{
    qsort(namess,k,sizeof(namess[0]),cmp);
    for(int i=0;i<k;i++){
        printf("%s\n",namess[i]);
    }
    }
}

L2-020 功夫传人

分数 35

全屏浏览

切换布局

作者陈越

单位浙江大学

一门武功能否传承久远并被发扬光大，是要看缘分的。一般来说，师傅传授给徒弟的武功总要打个折扣，于是越往后传，弟子们的功夫就越弱...... 直到某一支的某一代突然出现一个天分特别高的弟子（或者是吃到了灵丹、挖到了特别的秘笈），会将功夫的威力一下子放大N倍 ------ 我们称这种弟子为"得道者"。

这里我们来考察某一位祖师爷门下的徒子徒孙家谱：假设家谱中的每个人只有1位师傅（除了祖师爷没有师傅）；每位师傅可以带很多徒弟；并且假设辈分严格有序，即祖师爷这门武功的每个第i代传人只能在第i-1代传人中拜1个师傅。我们假设已知祖师爷的功力值为Z，每向下传承一代，就会减弱r%，除非某一代弟子得道。现给出师门谱系关系，要求你算出所有得道者的功力总值。

输入格式：

输入在第一行给出3个正整数，分别是：N（≤105）------整个师门的总人数（于是每个人从0到N−1编号，祖师爷的编号为0）；Z------祖师爷的功力值（不一定是整数，但起码是正数）；r ------每传一代功夫所打的折扣百分比值（不超过100的正数）。接下来有N行，第i行（i=0,⋯,N−1）描述编号为i的人所传的徒弟，格式为：

Ki ID[1] ID[2] ⋯ ID[Ki]

其中Ki是徒弟的个数，后面跟的是各位徒弟的编号，数字间以空格间隔。Ki为零表示这是一位得道者，这时后面跟的一个数字表示其武功被放大的倍数。

输出格式：

在一行中输出所有得道者的功力总值，只保留其整数部分。题目保证输入和正确的输出都不超过1010。

输入样例：

10 18.0 1.00
3 2 3 5
1 9
1 4
1 7
0 7
2 6 1
1 8
0 9
0 4
0 3

输出样例：

404

#include<stdio.h>
int fu[100000];
int dist[100000]={0};//意思是几代
int find(int x){
    if(x==fu[x])
        return x;
    else{
        int t=find(fu[x]);
        dist[x]=dist[x]+dist[fu[x]];
        fu[x]=t;//路径压缩了属于是，其实写不写无所谓
        return fu[x];
    }
}
void un(int u,int v){
    int fu1 = find(u);
    int fv1 = find(v);
    if(fu1 != fv1){
        fu[fv1] = fu1;
        dist[v] = dist[u] + 1;//这边v是弟子，u是师傅
    }
}
int main(){
    //原本是想直接模拟求解，先把关系找好然后直接从后往上找，后来想想直接用并查集也挺好
    //思路好像差不多
    int n;
    double z;
    double r;
    int cnt[100000]={0};
    scanf("%d %lf %lf",&n,&z,&r);
    for(int i=0;i<n;i++){
        fu[i]=i;
    }
    for(int i=0;i<n;i++){
        int k,x;
        scanf("%d",&k);
        if(k!=0){
            for(int j=0;j<k;j++){
                scanf("%d",&x);
                un(i,x);
            }
        }
        else{
            scanf("%d",&x);
            cnt[i]=x;//记录功力放大倍数
        }
    }
    double sum=0;
    double bilv=1-r/100;
    double bilvs[100000]={0};
    bilvs[0]=1;
    for(int i=1;i<=n;i++)
        bilvs[i] = bilv * bilvs[i - 1];//这边就是直接计算出第几代会损失多少功力
    for(int i=0;i<n;i++)
        if(cnt[i]!=0)
            sum+=z*bilvs[dist[i]]*cnt[i];
    printf("%d",(int)sum);
}

L2-021 点赞狂魔

分数 35

全屏浏览

切换布局

作者陈越

单位浙江大学

微博上有个"点赞"功能，你可以为你喜欢的博文点个赞表示支持。每篇博文都有一些刻画其特性的标签，而你点赞的博文的类型，也间接刻画了你的特性。然而有这么一种人，他们会通过给自己看到的一切内容点赞来狂刷存在感，这种人就被称为"点赞狂魔"。他们点赞的标签非常分散，无法体现出明显的特性。本题就要求你写个程序，通过统计每个人点赞的不同标签的数量，找出前3名点赞狂魔。

输入格式：

输入在第一行给出一个正整数N（≤100），是待统计的用户数。随后N行，每行列出一位用户的点赞标签。格式为"Name K F1⋯FK"，其中Name是不超过8个英文小写字母的非空用户名，1≤K≤1000，Fi（i=1,⋯,K）是特性标签的编号，我们将所有特性标签从 1 到 107 编号。数字间以空格分隔。

输出格式：

统计每个人点赞的不同标签的数量，找出数量最大的前3名，在一行中顺序输出他们的用户名,其间以1个空格分隔,且行末不得有多余空格。如果有并列，则输出标签出现次数平均值最小的那个，题目保证这样的用户没有并列。若不足3人，则用-补齐缺失，例如mike jenny -就表示只有2人。

输入样例：

5
bob 11 101 102 103 104 105 106 107 108 108 107 107
peter 8 1 2 3 4 3 2 5 1
chris 12 1 2 3 4 5 6 7 8 9 1 2 3
john 10 8 7 6 5 4 3 2 1 7 5
jack 9 6 7 8 9 10 11 12 13 14

输出样例：

jack chris john

#include<stdio.h>
typedef struct{
    char name[20];
    int sum;   //不同标签总数
    int num;    //点赞总数
    int f[1000];
}User;
int fact[100000000];
int main(){
    int n,k;
    scanf("%d",&n);
    User users[100];
    int i,j;
    for(i=0;i<n;i++){
        users[i].sum=0;
        scanf("%s",users[i].name);
        scanf("%d",&users[i].num);
        for(j=0;j<users[i].num;j++){
            scanf("%d",&users[i].f[j]);
            fact[users[i].f[j]]++;
            if(fact[users[i].f[j]]==1)
                users[i].sum++;
        }
       for(j=0;j<users[i].num;j++) //重新归0
            fact[users[i].f[j]]=0;
    }
    //进行排序(这边建议使用选择排序)
    int max;
    for(i=0;i<n-1;i++){
        max=i;
        for(j=i+1;j<n;j++){
            if(users[max].sum<users[j].sum)
                max=j;
            else if(users[max].sum==users[j].sum&&users[max].num>users[j].num)
                max=j;
        }
        User t=users[i];
        users[i]=users[max];
        users[max]=t;
    }
    if(n<3){
        for(i=0;i<n-1;i++)
            printf("%s ",users[i].name);
            printf("%s",users[n-1].name);
        for(i=0;i<3-n;i++)
            printf(" -");
    }
    else{
        printf("%s %s %s",users[0].name,users[1].name,users[2].name);
    }
    return 0;
}

L2-022 重排链表

分数 35

全屏浏览

切换布局

作者陈越

单位浙江大学

给定一个单链表 L1→L2→⋯→Ln−1→Ln，请编写程序将链表重新排列为 Ln→L1→Ln−1→L2→⋯。例如：给定L为1→2→3→4→5→6，则输出应该为6→1→5→2→4→3。

输入格式：

每个输入包含1个测试用例。每个测试用例第1行给出第1个结点的地址和结点总个数，即正整数N (≤105)。结点的地址是5位非负整数，NULL地址用−1表示。

接下来有N行，每行格式为：

Address Data Next

其中Address是结点地址；Data是该结点保存的数据，为不超过105的正整数；Next是下一结点的地址。题目保证给出的链表上至少有两个结点。

输出格式：

对每个测试用例，顺序输出重排后的结果链表，其上每个结点占一行，格式与输入相同。

输入样例：

00100 6
00000 4 99999
00100 1 12309
68237 6 -1
33218 3 00000
99999 5 68237
12309 2 33218

输出样例：

68237 6 00100
00100 1 99999
99999 5 12309
12309 2 00000
00000 4 33218
33218 3 -1

//这道题不一定一定要写一个链表，直接暴力求解
#include<stdio.h>
struct node{
    int id;
    int data;
    int next;
};
int main(){
    int start,n;
    struct node node[100005];
    scanf("%d %d",&start,&n);
    for(int i=0;i<n;i++){
        int t,x,y;
        scanf("%d %d %d",&t,&x,&y);
        node[t].id=t;
        node[t].data=x;
        node[t].next=y;
    }
    int a[100005];
    a[1]=start;
    int count=1;
    for(int i=2;i<=n;i++){
        if(node[start].next==-1){
            break;
        }
        a[i]=node[start].next;
        start=a[i];
        count++;
    }
    int b[100005];
    int num=1;
    if((count)%2==0){
        for(int i=1;i<=(count)/2;i++){
            b[num++]=a[count-i+1];
            b[num++]=a[i];
        }
    }
    else{
        for(int i=1;i<=(count)/2;i++){
            b[num++]=a[count-i+1];
            b[num++]=a[i];
        }
        b[num++]=a[(count)/2+1];
    }
    for(int i=1;i<=num-1;i++){
        printf("%05d %d ",b[i],node[b[i]].data);
        if(i!=num-1)
            printf("%05d\n",b[i+1]);
        else
            printf("-1");
    }
}

L2-023 图着色问题

分数 40

全屏浏览

切换布局

作者陈越

单位浙江大学

图着色问题是一个著名的NP完全问题。给定无向图G=(V,E)，问可否用K种颜色为V中的每一个顶点分配一种颜色，使得不会有两个相邻顶点具有同一种颜色？

但本题并不是要你解决这个着色问题，而是对给定的一种颜色分配，请你判断这是否是图着色问题的一个解。

输入格式：

输入在第一行给出3个整数V（0<V≤500）、E（≥0）和K（0<K≤V），分别是无向图的顶点数、边数、以及颜色数。顶点和颜色都从1到V编号。随后E行，每行给出一条边的两个端点的编号。在图的信息给出之后，给出了一个正整数N（≤20），是待检查的颜色分配方案的个数。随后N行，每行顺次给出V个顶点的颜色（第i个数字表示第i个顶点的颜色），数字间以空格分隔。题目保证给定的无向图是合法的（即不存在自回路和重边）。

输出格式：

对每种颜色分配方案，如果是图着色问题的一个解则输出Yes，否则输出No，每句占一行。

输入样例：

6 8 3
2 1
1 3
4 6
2 5
2 4
5 4
5 6
3 6
4
1 2 3 3 1 2
4 5 6 6 4 5
1 2 3 4 5 6
2 3 4 2 3 4

输出样例：

Yes
Yes
No
No

#include<iostream>
#include<set>
using namespace std;
int main(){
    int g[501][501];
    for(int i=0;i<501;i++){
        for(int j=0;j<501;j++){
            g[i][j]=0;
        }
    }
    int v,e,k;
    scanf("%d %d %d",&v,&e,&k);
    for(int i=0;i<e;i++){
        int x,y;
        scanf("%d %d",&x,&y);
        g[x][y]=1;
        g[y][x]=1;
    }
    int ce;
    scanf("%d",&ce);
    int yan[501]={0};
    for(int i=0;i<ce;i++){
        set<int> yanse;
        for(int j=1;j<=v;j++){
            scanf("%d",&yan[j]);
            yanse.insert(yan[j]);
        }
        int flag=0;
        if(yanse.size()!=k){
            printf("No\n");
            continue;
        }
        for(int l=1;l<=v;l++){
            for(int j=1;j<=v;j++){
                if(g[l][j]==1&&yan[l]==yan[j]){
                    printf("No\n");
                    flag=1;
                    break;
                }
            }
            if(flag==1)
                break;
        }
        if(flag==0)
            printf("Yes\n");
    }
}

L2-024 部落

分数 35

全屏浏览

切换布局

作者陈越

单位浙江大学

在一个社区里，每个人都有自己的小圈子，还可能同时属于很多不同的朋友圈。我们认为朋友的朋友都算在一个部落里，于是要请你统计一下，在一个给定社区中，到底有多少个互不相交的部落？并且检查任意两个人是否属于同一个部落。

输入格式：

输入在第一行给出一个正整数N（≤104），是已知小圈子的个数。随后N行，每行按下列格式给出一个小圈子里的人：

K P[1] P[2] ⋯ P[K]

其中K是小圈子里的人数，P[i]（i=1,⋯,K）是小圈子里每个人的编号。这里所有人的编号从1开始连续编号，最大编号不会超过104。

之后一行给出一个非负整数Q（≤104），是查询次数。随后Q行，每行给出一对被查询的人的编号。

输出格式：

首先在一行中输出这个社区的总人数、以及互不相交的部落的个数。随后对每一次查询，如果他们属于同一个部落，则在一行中输出Y，否则输出N。

输入样例：

输出样例：

10 2
Y
N

//讲真的这道题没什么难度，set计算人数+并查集秒了
#include<iostream>
#include<set>
using namespace std;
int fu[10001];
int find(int x){
    if(fu[x]==x)
        return x;
    else
        return find(fu[x]);
}
void un(int a,int b){
    int a1=find(a);
    int b1=find(b);
    if(a1!=b1){
        fu[a1]=b1;
    }
}
int main(){
    int N;
    cin>>N;
    set<int> s;
    for(int i=1;i<=10001;i++){
        fu[i]=i;
    }
    for(int i=0;i<N;i++){
        int k;
        cin>>k;
        int b[k];
        for(int j=0;j<k;j++){
            cin>>b[j];
            s.insert(b[j]);
            if(j>0){
                un(b[j-1],b[j]);
            }
        }
    }
    cout<<s.size()<<" ";
    int sum=0;
    for(int i=1;i<=s.size();i++){
        if(fu[i]==i)
            sum++;
    }
    cout<<sum<<endl;
    int chaxun;
    cin>>chaxun;
    for(int i=0;i<chaxun;i++){
        int a1,a2;
        cin>>a1>>a2;
        if(find(a1)==find(a2))
            cout<<"Y"<<endl;
        else
            cout<<"N"<<endl;
    }
}

L2-025 分而治之

分数 35

全屏浏览

切换布局

作者陈越

单位浙江大学

分而治之，各个击破是兵家常用的策略之一。在战争中，我们希望首先攻下敌方的部分城市，使其剩余的城市变成孤立无援，然后再分头各个击破。为此参谋部提供了若干打击方案。本题就请你编写程序，判断每个方案的可行性。

输入格式：

输入在第一行给出两个正整数 N 和 M（均不超过10 000），分别为敌方城市个数（于是默认城市从 1 到 N 编号）和连接两城市的通路条数。随后 M 行，每行给出一条通路所连接的两个城市的编号，其间以一个空格分隔。在城市信息之后给出参谋部的系列方案，即一个正整数 K （≤ 100）和随后的 K 行方案，每行按以下格式给出：

Np v[1] v[2] ... v[Np]

其中 Np 是该方案中计划攻下的城市数量，后面的系列 v[i] 是计划攻下的城市编号。

输出格式：

对每一套方案，如果可行就输出YES，否则输出NO。

输入样例：

10 11
8 7
6 8
4 5
8 4
8 1
1 2
1 4
9 8
9 1
1 10
2 4
5
4 10 3 8 4
6 6 1 7 5 4 9
3 1 8 4
2 2 8
7 9 8 7 6 5 4 2

输出样例：

NO
YES
YES
NO
NO

#include <iostream>
#include <vector>
using namespace std;
int main() {
    int n, m;
    cin>>n>>m;
    vector<int> v[10001];
    int vis[10001]={0};//未被攻占
    int t1,t2;
    while(m>0) {
        cin>>t1>>t2;
        v[t1].push_back(t2);
        v[t2].push_back(t1);
        m--;
    }
    int k=0;
    cin>>k;
    while(k>0){
        int num;
        cin>>num;
        while(num>0){
            int id;
            cin>>id;
            vis[id]=1;
            num--;
        }
        bool flag=true;
        for(int i=1;i<=n;i++){
            for (int j=0;j<v[i].size();j++){
                if (vis[i]==0&&vis[v[i][j]]==0){
                    //只要有一个没被攻占就是赢
                    flag=false;
                    break;
                }
            }
            if (flag==false){
                cout<<"NO"<< endl;
                break;
            }
        }
        if(flag==true)
            cout<<"YES"<<endl;
        for(int i=0;i<10001;i++){
            vis[i]=0;
        }
        k--;
    }
}

L2-026 小字辈

分数 35

全屏浏览

切换布局

作者陈越

单位浙江大学

本题给定一个庞大家族的家谱，要请你给出最小一辈的名单。

输入格式：

输入在第一行给出家族人口总数 N（不超过 100 000 的正整数） ------ 简单起见，我们把家族成员从 1 到 N 编号。随后第二行给出 N 个编号，其中第 i 个编号对应第 i 位成员的父/母。家谱中辈分最高的老祖宗对应的父/母编号为 -1。一行中的数字间以空格分隔。

输出格式：

首先输出最小的辈分（老祖宗的辈分为 1，以下逐级递增）。然后在第二行按递增顺序输出辈分最小的成员的编号。编号间以一个空格分隔，行首尾不得有多余空格。

输入样例：

9
2 6 5 5 -1 5 6 4 7

输出样例：

4
1 9

//这道题怎么说呢，跟并查集的思路有点像，具体思路可以参考功夫传人
//中间遇到数据过大超时的问题，已经解决，奖励自己一下
#include<iostream>
using namespace std;
int diema[100000];
int dist[100000]={0};
int find(int x){
    //这里假如我们已经计算出一个人的辈分就直接跳过，可以节约时间
    if(dist[x]==0){
        if(diema[x]==-1){
        dist[x]=1;
         return 1;
    }
    dist[x]=find(diema[x])+1;
    return dist[x];
    }
    return dist[x];
}
int main(){
    int n;
    cin>>n;
    for(int i=1;i<=n;i++){
        int t;
        cin>>t;
        diema[i]=t;
    }
    int max=-100;
    for(int i=1;i<=n;i++){
        dist[i]=find(i);//储存每个人的辈分
        if(max<dist[i])
            max=dist[i];
    }
    cout<<max<<endl;
    int sum=0;
    for(int i=1;i<=n;i++){
        if(dist[i]==max)
            sum++;
    }
    int count=0;
    for(int i=1;i<=n;i++){
        if(dist[i]==max&&(count+1)!=sum){
             cout<<i<<" ";
             count++;
        }
        else if(dist[i]==max&&(count+1)==sum){
            cout<<i;
            break;
        }
    }
}

L2-027 名人堂与代金券

分数 35

全屏浏览

切换布局

作者陈越

单位浙江大学

对于在中国大学MOOC（http://www.icourse163.org/ ）学习"数据结构"课程的学生，想要获得一张合格证书，总评成绩必须达到 60 分及以上，并且有另加福利：总评分在 [G, 100] 区间内者，可以得到 50 元 PAT 代金券；在 [60, G) 区间内者，可以得到 20 元PAT代金券。全国考点通用，一年有效。同时任课老师还会把总评成绩前 K 名的学生列入课程"名人堂"。本题就请你编写程序，帮助老师列出名人堂的学生，并统计一共发出了面值多少元的 PAT 代金券。

输入格式：

输入在第一行给出 3 个整数，分别是 N（不超过 10 000 的正整数，为学生总数）、G（在 (60,100) 区间内的整数，为题面中描述的代金券等级分界线）、K（不超过 100 且不超过 N 的正整数，为进入名人堂的最低名次）。接下来 N 行，每行给出一位学生的账号（长度不超过15位、不带空格的字符串）和总评成绩（区间 [0, 100] 内的整数），其间以空格分隔。题目保证没有重复的账号。

输出格式：

首先在一行中输出发出的 PAT 代金券的总面值。然后按总评成绩非升序输出进入名人堂的学生的名次、账号和成绩，其间以 1 个空格分隔。需要注意的是：成绩相同的学生享有并列的排名，排名并列时，按账号的字母序升序输出。

输入样例：

10 80 5
cy@zju.edu.cn 78
cy@pat-edu.com 87
1001@qq.com 65
uh-oh@163.com 96
test@126.com 39
anyone@qq.com 87
zoe@mit.edu 80
jack@ucla.edu 88
bob@cmu.edu 80
ken@163.com 70

输出样例：

360
1 uh-oh@163.com 96
2 jack@ucla.edu 88
3 anyone@qq.com 87
3 cy@pat-edu.com 87
5 bob@cmu.edu 80
5 zoe@mit.edu 80

#include<iostream>
#include <algorithm>
using namespace std;
struct student{
    string a;
    int b;
};
bool cmp(struct student x,struct student y){
    if(x.b!=y.b)
        return x.b>y.b;//降序
    if(x.b==y.b){
        return x.a<y.a;//升序
    }
}
int main(){
    int n,g,k;
    cin>>n>>g>>k;
    struct student s[n];
    int sum=0;
    for(int i=0;i<n;i++){
        cin>>s[i].a>>s[i].b;
        if(s[i].b>=g)
            sum=sum+50;
        else if(s[i].b<g&&s[i].b>=60)
            sum=sum+20;
    }
    sort(s,s+n,cmp);
    cout<<sum<<endl;
    int paiming=1;
    int j;
    int r=1;
    cout<<paiming<<' '<<s[0].a<<' '<<s[0].b<<endl;
    for(int i=1;i<n;i++){
        if(s[i].b==s[i-1].b){
            cout<<paiming<<' '<<s[i].a<<' '<<s[i].b<<endl;
            r++;
        }
        else{
            paiming=r;
            if(paiming>k)
                break;
            cout<<paiming+1<<' '<<s[i].a<<' '<<s[i].b<<endl;
            paiming++;
            r++;
        }
    }
}

L2-028 秀恩爱分得快

分数 35

全屏浏览

切换布局

作者陈越

单位浙江大学

古人云：秀恩爱，分得快。

互联网上每天都有大量人发布大量照片，我们通过分析这些照片，可以分析人与人之间的亲密度。如果一张照片上出现了 K 个人，这些人两两间的亲密度就被定义为 1/K。任意两个人如果同时出现在若干张照片里，他们之间的亲密度就是所有这些同框照片对应的亲密度之和。下面给定一批照片，请你分析一对给定的情侣，看看他们分别有没有亲密度更高的异性朋友？

输入格式：

输入在第一行给出 2 个正整数：N（不超过1000，为总人数------简单起见，我们把所有人从 0 到 N-1 编号。为了区分性别，我们用编号前的负号表示女性）和 M（不超过1000，为照片总数）。随后 M 行，每行给出一张照片的信息，格式如下：

K P[1] ... P[K]

其中 K（≤ 500）是该照片中出现的人数，P[1] ~ P[K] 就是这些人的编号。最后一行给出一对异性情侣的编号 A 和 B。同行数字以空格分隔。题目保证每个人只有一个性别，并且不会在同一张照片里出现多次。

输出格式：

首先输出 A PA，其中 PA 是与 A 最亲密的异性。如果 PA 不唯一，则按他们编号的绝对值递增输出；然后类似地输出 B PB。但如果 A 和 B 正是彼此亲密度最高的一对，则只输出他们的编号，无论是否还有其他人并列。

输入样例 1：

10 4
4 -1 2 -3 4
4 2 -3 -5 -6
3 2 4 -5
3 -6 0 2
-3 2

输出样例 1：

-3 2
2 -5
2 -6

输入样例 2：

4 4
4 -1 2 -3 0
2 0 -3
2 2 -3
2 -1 2 
-3 2

输出样例 2：

-3 2

#include <iostream>
using namespace std;

int zhuanhua(string s){
    int x=0;
    if(s[0]=='-'){
         for(int i=1;i<s.size();i++){
             x*=10;
             x+=s[i]-'0';
         }
    }
    else{
        for(int i=0;i<s.size();i++){
            x*=10;
            x+=s[i]-'0';
        }
    }
    return x;
}

int main(){
    int n,m;
    cin>>n>>m;
    double g[n][n];
    for(int i=0;i<n;i++){
        for(int j=0;j<n;j++){
            g[i][j]=0;
        }
    }
    string ct[n];
    int xb[n];
    while(m--){
        int k;
        cin>>k;
        int a[k];
        for(int i=0;i<k;i++){
            string t;
            cin>>t;
            int tn=zhuanhua(t);
            if(t[0]=='-')
                xb[tn]=1;
            else
                xb[tn]=2;
            a[i]=tn;//储存人的编号
        }
        double qingmi=1.0/k;
        for(int i=0;i<k-1;++i){
            for(int j=i+1;j<k;++j){
                if(xb[a[i]]==xb[a[j]])
                    continue;
                g[a[i]][a[j]]+=qingmi;//亲密度计算
                g[a[j]][a[i]]=g[a[i]][a[j]];
            }
        }
    }
    int x,y;
    string t;
    cin>>t;
    x=zhuanhua(t);
    if(t[0]=='-')
        xb[x]=1;
    else
        xb[x]=2;
    cin>>t;
    y=zhuanhua(t);
    if(t[0]=='-')
        xb[y]=1;
    else
        xb[y]=2;
    for(int i=0;i<n;i++){
        if(xb[i]==1)
            ct[i]="-";
        else
            ct[i]="";
    }
    double ma=0;
    double mb=0;//x,y的最大亲密度 
    for(int i=0;i<n;i++){
        if(xb[i]!=xb[x])
            ma=max(ma,g[x][i]);
    }
    for(int i=0;i<n;i++){
        if(xb[i]!=xb[y])
            mb=max(mb,g[y][i]);
    }
    if(ma==mb&&g[x][y]==ma)
        cout<<ct[x]<<x<<" "<<ct[y]<<y<<endl;
    else{
        for(int i=0;i<n;i++){
            if(g[x][i]==ma&&xb[x]!=xb[i])
                cout<<ct[x]<<x<<" "<<ct[i]<<i<<endl;
        }
        for(int i=0;i<n;i++){
            if(g[y][i]==mb&&xb[y]!=xb[i])
                cout<<ct[y]<<y<<" "<<ct[i]<<i<<endl;
        }
    }
}

L2-029 特立独行的幸福

分数 25

全屏浏览

切换布局

作者陈越

单位浙江大学

对一个十进制数的各位数字做一次平方和，称作一次迭代。如果一个十进制数能通过若干次迭代得到 1，就称该数为幸福数。1 是一个幸福数。此外，例如 19 经过 1 次迭代得到 82，2 次迭代后得到 68，3 次迭代后得到 100，最后得到 1。则 19 就是幸福数。显然，在一个幸福数迭代到 1 的过程中经过的数字都是幸福数，它们的幸福是依附于初始数字的。例如 82、68、100 的幸福是依附于 19 的。而一个特立独行 的幸福数，是在一个有限的区间内不依附于任何其它数字的；其独立性就是依附于它的的幸福数的个数。如果这个数还是个素数，则其独立性加倍。例如 19 在区间[1, 100] 内就是一个特立独行的幸福数，其独立性为 2×4=8。

另一方面，如果一个大于1的数字经过数次迭代后进入了死循环，那这个数就不幸福。例如 29 迭代得到 85、89、145、42、20、4、16、37、58、89、...... 可见 89 到 58 形成了死循环，所以 29 就不幸福。

本题就要求你编写程序，列出给定区间内的所有特立独行的幸福数和它的独立性。

输入格式：

输入在第一行给出闭区间的两个端点：1<A<B≤104。

输出格式：

按递增顺序列出给定闭区间 [A,B] 内的所有特立独行的幸福数和它的独立性。每对数字占一行，数字间以 1 个空格分隔。

如果区间内没有幸福数，则在一行中输出 SAD。

输入样例 1：

10 40

输出样例 1：

**注意：**样例中，10、13 也都是幸福数，但它们分别依附于其他数字（如 23、31 等等），所以不输出。其它数字虽然其实也依附于其它幸福数，但因为那些数字不在给定区间 [10, 40] 内，所以它们在给定区间内是特立独行的幸福数。

输入样例 2：

110 120

输出样例 2：

SAD

#include<iostream>
#include<set>
#include<cmath>
using namespace std;
int count[10000]={0};//依赖个数
int diedai(int x){
    int x1=x;
    set<int> s;//用来判断是否进入死循环
    while(x!=1){
        int sum=0;
        while(x>0){
            sum+=(x%10)*(x%10);
            x=x/10;
        }
        pair<set<int>::iterator,bool> pr=s.insert(sum);
        if(pr.second==false)
            return 0;//表明进入死循环
        x=sum;
    }
    count[x1]=s.size();
    return 1;
}
int panduan(int a,int b){  //用来判断a是不是依赖b
    while(b!=1){
        int sum=0;
        while(b>0){
            sum+=(b%10)*(b%10);
            b=b/10;
        }
        b=sum;
        if(a==b)
            return 1;
    }
    return 0;
}
int panduansushu(int x){
     if(x==1)
        return 0;
    for(int i=2;i<=sqrt(x);i++){
        if(x%i==0)
            return 0;
    }
    return 1;//意思是是素数
}
int main(){
    int a1,b;
    cin>>a1>>b;
    int a[10000];//储存幸福数
    int num=0;//用来记录幸福数个数
    for(int i=a1;i<=b;i++){
        if(diedai(i)==1){
            a[num++]=i;
        }
    }
    if(num==0){
        cout<<"SAD";
        return 0;
    }
    for(int i=0;i<num;i++){
        int flag=0;
        for(int j=0;j<num;j++){
            if(i==j)
                continue;
            if(panduan(a[i],a[j])!=0){
                flag=1;
                break;
            }
        }
        if(flag==0){
            cout<<a[i]<<" ";
            if(panduansushu(a[i])==1)
                cout<<count[a[i]]*2<<endl;
            else
                cout<<count[a[i]]<<endl;
        }
    }
}

L2-030 冰岛人

分数 35

全屏浏览

切换布局

作者陈越

单位浙江大学

2018年世界杯，冰岛队因1:1平了强大的阿根廷队而一战成名。好事者发现冰岛人的名字后面似乎都有个"松"（son），于是有网友科普如下：

冰岛人沿用的是维京人古老的父系姓制，孩子的姓等于父亲的名加后缀，如果是儿子就加 sson，女儿则加 sdottir。因为冰岛人口较少，为避免近亲繁衍，本地人交往前先用个 App 查一下两人祖宗若干代有无联系。本题就请你实现这个 App 的功能。

输入格式：

输入首先在第一行给出一个正整数 N（1<N≤105），为当地人口数。随后 N 行，每行给出一个人名，格式为：名姓（带性别后缀），两个字符串均由不超过 20 个小写的英文字母组成。维京人后裔是可以通过姓的后缀判断其性别的，其他人则是在姓的后面加 m 表示男性、f 表示女性。题目保证给出的每个维京家族的起源人都是男性。

随后一行给出正整数 M，为查询数量。随后 M 行，每行给出一对人名，格式为：名1 姓1 名2 姓2。注意：这里的姓是不带后缀的。四个字符串均由不超过 20 个小写的英文字母组成。

题目保证不存在两个人是同名的。

输出格式：

对每一个查询，根据结果在一行内显示以下信息：

若两人为异性，且五代以内无公共祖先，则输出 Yes；
若两人为异性，但五代以内（不包括第五代）有公共祖先，则输出 No；
若两人为同性，则输出 Whatever；
若有一人不在名单内，则输出 NA。

所谓"五代以内无公共祖先"是指两人的公共祖先（如果存在的话）必须比任何一方的曾祖父辈分高。

输入样例：

15
chris smithm
adam smithm
bob adamsson
jack chrissson
bill chrissson
mike jacksson
steve billsson
tim mikesson
april mikesdottir
eric stevesson
tracy timsdottir
james ericsson
patrick jacksson
robin patricksson
will robinsson
6
tracy tim james eric
will robin tracy tim
april mike steve bill
bob adam eric steve
tracy tim tracy tim
x man april mikes

输出样例：

Yes
No
No
Whatever
Whatever
NA

//这道题也是比较简单的，就类似于并查集的思路然后就是额
//主要是这个性别和姓名可能有点难处理，看了网上可以采用map，即爹当键，人名当值
#include<iostream>
#include<map>
#include<string>
using namespace std;
struct Peoson {
    char sex;
    string father;
};
map<string,struct Peoson> people;
int panduan(string a,string b){
    string A=a;
    for (int i=1;!A.empty();i++){
        string B = b;
        for (int j=1;!B.empty();j++){
            if (i >= 5 && j >= 5)
                return 1;
            if (A == B && (i < 5 || j < 5))
                return 0;
            B = people[B].father;
        }
        A=people[A].father;
    }
    return 1;
}
int main(){
    int n,m;
    string str,a,b;
    cin >> n;
    for(int i=0;i<n;i++){
        cin >> a >> b;
        if(b[b.length()-1]=='n')
            people[a] = {'m',b.substr(0,b.size() - 4) };
        else if(b[b.length()-1]=='r')
            people[a] = { 'f',b.substr(0, b.size() - 7) };
        else
            people[a].sex = b[b.length()-1];
    }
    cin>>m;
    for (int i=0;i<m;i++) {
        cin >>a>>str>>b>>str;//姓氏没用啊
        if (people.find(a) == people.end() || people.find(b) == people.end())
            printf("NA\n");
        else if (people[a].sex == people[b].sex)
            printf("Whatever\n");
        else
            printf("%s\n", panduan(a,b)?"Yes":"No");
    }
}

L2-031 深入虎穴

分数 40

全屏浏览

切换布局

作者陈越

单位浙江大学

著名的王牌间谍 007 需要执行一次任务，获取敌方的机密情报。已知情报藏在一个地下迷宫里，迷宫只有一个入口，里面有很多条通路，每条路通向一扇门。每一扇门背后或者是一个房间，或者又有很多条路，同样是每条路通向一扇门...... 他的手里有一张表格，是其他间谍帮他收集到的情报，他们记下了每扇门的编号，以及这扇门背后的每一条通路所到达的门的编号。007 发现不存在两条路通向同一扇门。

内线告诉他，情报就藏在迷宫的最深处。但是这个迷宫太大了，他需要你的帮助 ------ 请编程帮他找出距离入口最远的那扇门。

输入格式：

输入首先在一行中给出正整数 N（<105），是门的数量。最后 N 行，第 i 行（1≤i≤N）按以下格式描述编号为 i 的那扇门背后能通向的门：

K D[1] D[2] ... D[K]

其中 K 是通道的数量，其后是每扇门的编号。

输出格式：

在一行中输出距离入口最远的那扇门的编号。题目保证这样的结果是唯一的。

输入样例：

输出样例：

12

//这道题也不难说白了就是深搜算最大节点就好了
#include<iostream>
#include<vector>
using namespace std;
vector<int> v[100001];//图
int visit[100001]={0};
int cengshu=0;
int bianhao;
void dfs(int start,int cnt){
    if(cnt>cengshu){
        cengshu=cnt;
        bianhao=start;
    }
    for(int i=0;i<v[start].size();i++){
        dfs(v[start][i],cnt+1);
    }
}
int main(){
    int n;
    cin>>n;
    for(int i=1;i<=n;i++){
        int k;
        cin>>k;
        for(int j=0;j<k;j++){
            int t;
            cin>>t;
            visit[t]=1;//意味着额这扇门被其他门通过，我们需要找到最开始的们
            v[i].push_back(t);
        }
    }
    int start;
    for(int i=1;i<=n;i++){
        if(visit[i]==0){
            start=i;
            break;
        }
    }
    dfs(start,1);
    cout<<bianhao;
}

L2-032 彩虹瓶

分数 25

全屏浏览

切换布局

作者陈越

单位浙江大学

彩虹瓶的制作过程（并不）是这样的：先把一大批空瓶铺放在装填场地上，然后按照一定的顺序将每种颜色的小球均匀撒到这批瓶子里。

假设彩虹瓶里要按顺序装 N 种颜色的小球（不妨将顺序就编号为 1 到 N）。现在工厂里有每种颜色的小球各一箱，工人需要一箱一箱地将小球从工厂里搬到装填场地。如果搬来的这箱小球正好是可以装填的颜色，就直接拆箱装填；如果不是，就把箱子先码放在一个临时货架上，码放的方法就是一箱一箱堆上去。当一种颜色装填完以后，先看看货架顶端的一箱是不是下一个要装填的颜色，如果是就取下来装填，否则去工厂里再搬一箱过来。

如果工厂里发货的顺序比较好，工人就可以顺利地完成装填。例如要按顺序装填 7 种颜色，工厂按照 7、6、1、3、2、5、4 这个顺序发货，则工人先拿到 7、6 两种不能装填的颜色，将其按照 7 在下、6 在上的顺序堆在货架上；拿到 1 时可以直接装填；拿到 3 时又得临时码放在 6 号颜色箱上；拿到 2 时可以直接装填；随后从货架顶取下 3 进行装填；然后拿到 5，临时码放到 6 上面；最后取了 4 号颜色直接装填；剩下的工作就是顺序从货架上取下 5、6、7 依次装填。

但如果工厂按照 3、1、5、4、2、6、7 这个顺序发货，工人就必须要愤怒地折腾货架了，因为装填完 2 号颜色以后，不把货架上的多个箱子搬下来就拿不到 3 号箱，就不可能顺利完成任务。

另外，货架的容量有限，如果要堆积的货物超过容量，工人也没办法顺利完成任务。例如工厂按照 7、6、5、4、3、2、1 这个顺序发货，如果货架够高，能码放 6 只箱子，那还是可以顺利完工的；但如果货架只能码放 5 只箱子，工人就又要愤怒了......

本题就请你判断一下，工厂的发货顺序能否让工人顺利完成任务。

输入格式：

输入首先在第一行给出 3 个正整数，分别是彩虹瓶的颜色数量 N（1<N≤103）、临时货架的容量 M（<N）、以及需要判断的发货顺序的数量 K。

随后 K 行，每行给出 N 个数字，是 1 到N 的一个排列，对应工厂的发货顺序。

一行中的数字都以空格分隔。

输出格式：

对每个发货顺序，如果工人可以愉快完工，就在一行中输出 YES；否则输出 NO。

输入样例：

7 5 3
7 6 1 3 2 5 4
3 1 5 4 2 6 7
7 6 5 4 3 2 1

输出样例：

YES
NO
NO

#include<iostream>
#include<stack>
using namespace std;
int main(){
    int n,m,k;
    cin>>n>>m>>k;
    while (k--){
        int now=1;
        int a[1001];
        stack<int> s;
        for(int i=0;i<n;i++)
            cin>>a[i];
        for(int i=0;i<n;i++){
            if(a[i]==now){
                now++;
                while(s.empty()==false&&s.top()==now){
                    s.pop();
                    now++;
                }
            }
            else{
                s.push(a[i]);
                if(s.size()>m)
                    break; //超出容量直接结束
            }
        }
        if(now<n+1)
            cout<<"NO"<< endl;
        else
            cout<<"YES"<<endl;
    }
}

L2-033 简单计算器

分数 25

全屏浏览

切换布局

作者陈越

单位浙江大学

本题要求你为初学数据结构的小伙伴设计一款简单的利用堆栈执行的计算器。如上图所示，计算器由两个堆栈组成，一个堆栈 S1 存放数字，另一个堆栈 S2 存放运算符。计算器的最下方有一个等号键，每次按下这个键，计算器就执行以下操作：

从 S1 中弹出两个数字，顺序为 n1 和 n2；
从 S2 中弹出一个运算符 op；
执行计算 n2 op n1；
将得到的结果压回 S1。

直到两个堆栈都为空时，计算结束，最后的结果将显示在屏幕上。

输入格式：

输入首先在第一行给出正整数 N（1<N≤103），为 S1 中数字的个数。

第二行给出 N 个绝对值不超过 100 的整数；第三行给出 N−1 个运算符 ------ 这里仅考虑 +、-、*、/ 这四种运算。一行中的数字和符号都以空格分隔。

输出格式：

将输入的数字和运算符按给定顺序分别压入堆栈 S1 和 S2，将执行计算的最后结果输出。注意所有的计算都只取结果的整数部分。题目保证计算的中间和最后结果的绝对值都不超过 109。

如果执行除法时出现分母为零的非法操作，则在一行中输出：ERROR: X/0，其中 X 是当时的分子。然后结束程序。

输入样例 1：

5
40 5 8 3 2
/ * - +

输出样例 1：

输入样例 2：

5
2 5 8 4 4
* / - +

输出样例 2：

ERROR: 5/0

#include<iostream>
#include<stack>
using namespace std;
int main(){
    stack<int> s1;
    stack<char> s2;
    int n;
    cin>>n;
    for(int i=0;i<n;i++){
        int t;
        cin>>t;
        s1.push(t);
    }
    for(int i=0;i<n-1;i++){
        char c;
        cin>>c;
        s2.push(c);
    }
    int flag=0;
    while(s2.empty()==false){
        int n1,n2;
        n1=s1.top();
        s1.pop();
        n2=s1.top();
        s1.pop();
        char c=s2.top();
        s2.pop();
        if(c=='*'){
            s1.push(n1*n2);
        }
        else if(c=='+'){
            s1.push(n1+n2);
        }
        else if(c=='-'){
            s1.push(n2-n1);
        }
        else{
            if(n1==0){
                printf("ERROR: %d/0",n2);
                flag=1;
                break;
            }
            else
                s1.push(n2/n1);
        }
    }
    if(flag==0)
    cout<<s1.top();
}

L2-034 口罩发放

分数 25

全屏浏览

切换布局

作者 DAI, Longao

单位杭州百腾教育科技有限公司

为了抗击来势汹汹的 COVID19 新型冠状病毒，全国各地均启动了各项措施控制疫情发展，其中一个重要的环节是口罩的发放。

某市出于给市民发放口罩的需要，推出了一款小程序让市民填写信息，方便工作的开展。小程序收集了各种信息，包括市民的姓名、身份证、身体情况、提交时间等，但因为数据量太大，需要根据一定规则进行筛选和处理，请你编写程序，按照给定规则输出口罩的寄送名单。

输入格式:

输入第一行是两个正整数 D 和 P（1≤D,P≤30），表示有 D 天的数据，市民两次获得口罩的时间至少需要间隔 P 天。

接下来 D 块数据，每块给出一天的申请信息。第 i 块数据（i=1,⋯,D）的第一行是两个整数 Ti 和 Si（1≤Ti,Si≤1000），表示在第 i 天有 Ti 条申请，总共有 Si 个口罩发放名额。随后 Ti 行，每行给出一条申请信息，格式如下：

姓名 身份证号 身体情况 提交时间

给定数据约束如下：

姓名 是一个长度不超过 10 的不包含空格的非空字符串；
身份证号 是一个长度不超过 20 的非空字符串；
身体情况 是 0 或者 1，0 表示自觉良好，1 表示有相关症状；
提交时间 是 hh:mm，为24小时时间（由 00:00 到 23:59。例如 09:08。）。注意，给定的记录的提交时间不一定有序；
身份证号 各不相同，同一个身份证号被认为是同一个人，数据保证同一个身份证号姓名是相同的。

能发放口罩的记录要求如下：

身份证号 必须是 18 位的数字（可以包含前导0）；
同一个身份证号若在第 i 天申请成功，则接下来的 P 天不能再次申请。也就是说，若第 i 天申请成功，则等到第 i+P+1 天才能再次申请；
在上面两条都符合的情况下，按照提交时间的先后顺序发放，直至全部记录处理完毕或 Si 个名额用完。如果提交时间相同，则按照在列表中出现的先后顺序决定。

输出格式:

对于每一天的申请记录，每行输出一位得到口罩的人的姓名及身份证号，用一个空格隔开。顺序按照发放顺序确定。

在输出完发放记录后，你还需要输出有合法记录的、身体状况为 1 的申请人的姓名及身份证号，用空格隔开。顺序按照申请记录中出现的顺序确定，同一个人只需要输出一次。

输入样例:

4 2
5 3
A 123456789012345670 1 13:58
B 123456789012345671 0 13:58
C 12345678901234567 0 13:22
D 123456789012345672 0 03:24
C 123456789012345673 0 13:59
4 3
A 123456789012345670 1 13:58
E 123456789012345674 0 13:59
C 123456789012345673 0 13:59
F F 0 14:00
1 3
E 123456789012345674 1 13:58
1 1
A 123456789012345670 0 14:11

输出样例:

D 123456789012345672
A 123456789012345670
B 123456789012345671
E 123456789012345674
C 123456789012345673
A 123456789012345670
A 123456789012345670
E 123456789012345674

样例解释：

输出中，第一行到第三行是第一天的部分；第四、五行是第二天的部分；第三天没有符合要求的市民；第六行是第四天的部分。最后两行按照出现顺序输出了可能存在身体不适的人员。

//其实这道题本身不难就是有点复杂，注意一点就行了
#include<iostream>
#include<algorithm>
#include<vector>
#include<map>
using namespace std;
struct person{ 
    string name;
    string id;
    string time;
    int heal;
    int order;//身体情况，列表中出现顺序   
};
map<string,int> ca;  //这是为了记录人和申请时间
vector<struct person> v;  //人
map<string,string> card;   //单纯是用来记录有病症的人的身份证
vector<string> bing;       //记录有症状的人

bool cmp(struct person c,struct person d){
    if(c.time!=d.time)
        return c.time<d.time;//先比时间升序
    else 
        return c.order<d.order;//在比在列表中出现顺序
}

int check(string shengfen){
    if(shengfen.length()!=18)
        return 0;
    for(int i=0;i<18;i++){
        if(shengfen[i]<'0'||shengfen[i]>'9')//不是数字就去世
            return 0;
    }
    return 1;
}

int main(){
   int d,p;
   struct person a;
   cin>>d>>p;
    for(int i=1;i<=d;i++){
        int t,s;
        cin>>t>>s;
        for(int j=1;j<=t;j++){
          cin>>a.name>>a.id>>a.heal>>a.time; 
          a.order=j;
          if(check(a.id)==1){//判断身份证是否合法
              if(a.heal==1&&find(bing.begin(),bing.end(),a.id)==bing.end()){  //身体有状况同时不在bing之中
                  card[a.id]=a.name;
                  bing.push_back(a.id);
              }
              v.push_back(a);
          }
        }
        sort(v.begin(),v.end(),cmp);//排序
        for(auto j:v){
            if(s==0)
                break;//口罩发完
            if(ca.find(j.id)==ca.end()||ca[j.id]<=i){
                cout<<j.name<<" "<<j.id<<endl;
                ca[j.id]=i+p+1;//更新可申请日期
                s--;
            }
        }
        v.clear();//清空
    }
    for(auto j:bing)
        cout<<card[j]<<" "<<j<<endl;
}

L2-035 完全二叉树的层序遍历

分数 35

全屏浏览

切换布局

作者陈越

单位浙江大学

一个二叉树，如果每一个层的结点数都达到最大值，则这个二叉树就是完美二叉树 。对于深度为 D 的，有 N 个结点的二叉树，若其结点对应于相同深度完美二叉树的层序遍历的前 N 个结点，这样的树就是完全二叉树。

给定一棵完全二叉树的后序遍历，请你给出这棵树的层序遍历结果。

输入格式：

输入在第一行中给出正整数 N（≤30），即树中结点个数。第二行给出后序遍历序列，为 N 个不超过 100 的正整数。同一行中所有数字都以空格分隔。

输出格式：

在一行中输出该树的层序遍历序列。所有数字都以 1 个空格分隔，行首尾不得有多余空格。

输入样例：

8
91 71 2 34 10 15 55 18

输出样例：

18 34 55 71 2 10 15 91

#include<stdio.h>
struct tree1{
    int val;
    int left;
    int right;
};
typedef struct tree1 tree;
tree a[100];

void bianli(int index){
    if(index!=-1){
    bianli(a[index].left);
    bianli(a[index].right);
    scanf("%d",&a[index].val);
    }
}
int main(){
    int N;
    scanf("%d",&N);
    for(int i=1;i<=N;i++){
        if(i*2<=N)  //左
            a[i].left=2*i;
        else
            a[i].left=-1;
        if(i*2+1<=N) //右
            a[i].right=2*i+1;
        else
            a[i].right=-1;
    }
    bianli(1);
    for(int i=1;i<N;i++){
        printf("%d ",a[i].val);
    }
    printf("%d",a[N].val);
}

L2-036 网红点打卡攻略

分数 35

全屏浏览

切换布局

作者陈越

单位浙江大学

一个旅游景点，如果被带火了的话，就被称为"网红点"。大家来网红点游玩，俗称"打卡"。在各个网红点打卡的快（省）乐（钱）方法称为"攻略"。你的任务就是从一大堆攻略中，找出那个能在每个网红点打卡仅一次、并且路上花费最少的攻略。

输入格式：

首先第一行给出两个正整数：网红点的个数 N（1<N≤200）和网红点之间通路的条数 M。随后 M 行，每行给出有通路的两个网红点、以及这条路上的旅行花费（为正整数），格式为"网红点1 网红点2 费用"，其中网红点从 1 到 N 编号；同时也给出你家到某些网红点的花费，格式相同，其中你家的编号固定为 0。

再下一行给出一个正整数 K，是待检验的攻略的数量。随后 K 行，每行给出一条待检攻略，格式为：

n V1 V2 ⋯ Vn

其中 n(≤200) 是攻略中的网红点数，Vi 是路径上的网红点编号。这里假设你从家里出发，从 V1 开始打卡，最后从 Vn 回家。

输出格式：

在第一行输出满足要求的攻略的个数。

在第二行中，首先输出那个能在每个网红点打卡仅一次、并且路上花费最少的攻略的序号（从 1 开始），然后输出这个攻略的总路费，其间以一个空格分隔。如果这样的攻略不唯一，则输出序号最小的那个。

题目保证至少存在一个有效攻略，并且总路费不超过 109。

输入样例：

6 13
0 5 2
6 2 2
6 0 1
3 4 2
1 5 2
2 5 1
3 1 1
4 1 2
1 6 1
6 3 2
1 2 1
4 5 3
2 0 2
7
6 5 1 4 3 6 2
6 5 2 1 6 3 4
8 6 2 1 6 3 4 5 2
3 2 1 5
6 6 1 3 4 5 2
7 6 2 1 3 4 5 2
6 5 2 1 4 3 6

输出样例：

3
5 11

样例说明：

第 2、3、4、6 条都不满足攻略的基本要求，即不能做到从家里出发，在每个网红点打卡仅一次，且能回到家里。所以满足条件的攻略有 3 条。

第 1 条攻略的总路费是：(0->5) 2 + (5->1) 2 + (1->4) 2 + (4->3) 2 + (3->6) 2 + (6->2) 2 + (2->0) 2 = 14；

第 5 条攻略的总路费同理可算得：1 + 1 + 1 + 2 + 3 + 1 + 2 = 11，是一条更省钱的攻略；

第 7 条攻略的总路费同理可算得：2 + 1 + 1 + 2 + 2 + 2 + 1 = 11，与第 5 条花费相同，但序号较大，所以不输出。

//这题没什么难度，邻接矩阵秒了，直接模拟就行
//致命错误就算你打算结束这条路径也要把后面的读取完
#include<iostream>
#include<set>
using namespace std;
int main(){
    int n,m;
    cin>>n>>m;
    int g[n+1][n+1];
    for(int i=0;i<n+1;i++){
        for(int j=0;j<n+1;j++){
            g[i][j]=-1;//初始化
        }
    }
    for(int i=0;i<m;i++){
        int x,y,f;
        cin>>x>>y>>f;
        g[x][y]=f;
        g[y][x]=f;
    }
    int count;
    cin>>count;
    int min=1000000000;//用来记录最小费用
    int index;//用来记录攻略编号
    int co=0;
    for(int i=0;i<count;i++){
        set<int> s;//这个是为了确保每个打卡点都出现了
        int flag=0;//如果出现等于1就直接爆炸
        int sum=0;
        int gongluedian;
        cin>>gongluedian;
        if(gongluedian!=n){  //直接跳过不做评价
            flag=1;
            for(int j=0;j<gongluedian;j++){
                int t;
                cin>>t;
            }
        }
        else{
            int pre;//用来记录前一个点
            for(int j=0;j<gongluedian;j++){
                int t;
                cin>>t;
                if(j==0){
                    if(g[t][0]==-1){
                        flag=1;
                        continue;
                    }
                    else{
                        pre=t;
                        s.insert(t);
                        sum+=g[t][0];
                    }
                }
                else if(j==gongluedian-1){
                    if(g[t][0]==-1){
                        flag=1;
                        continue;
                    }
                    else
                        sum+=g[t][0];
                    
                    if(g[pre][t]==-1){
                        flag=1;
                       continue;
                    }
                    else{
                        s.insert(t);
                        sum+=g[pre][t];
                        pre=t;
                    }
                }
                else{
                    if(g[pre][t]==-1){
                        flag=1;
                        continue;
                    }
                    else{
                        s.insert(t);
                        sum+=g[pre][t];
                        pre=t;
                    }
                }
            }
        }
        if(flag==0&&s.size()==n){
            co++;
            if(sum<min){
                min=sum;
                index=i+1;
            }
            else if(sum==min&&index>i+1){
                index=i+1;
            }
        }
    }
    cout<<co<<endl;
    cout<<index<<" "<<min;
}

L2-037 包装机

分数 35

全屏浏览

切换布局

作者陈越

单位浙江大学

一种自动包装机的结构如图 1 所示。首先机器中有 N 条轨道，放置了一些物品。轨道下面有一个筐。当某条轨道的按钮被按下时，活塞向左推动，将轨道尽头的一件物品推落筐中。当 0 号按钮被按下时，机械手将抓取筐顶部的一件物品，放到流水线上。图 2 显示了顺序按下按钮 3、2、3、0、1、2、0 后包装机的状态。

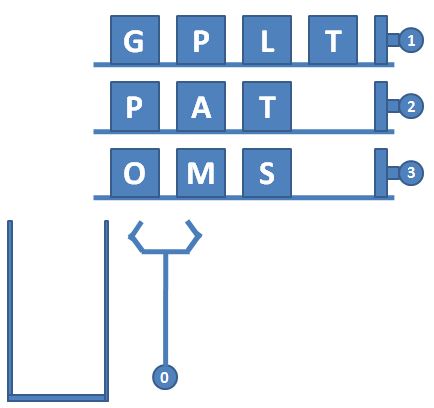
图1 自动包装机的结构

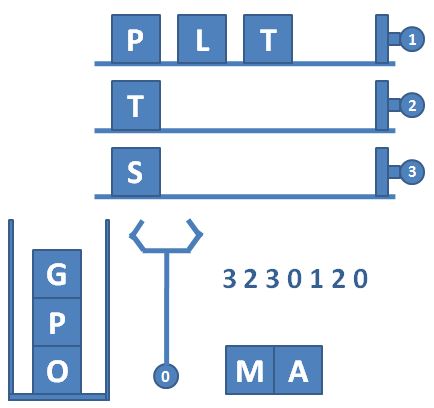
图 2 顺序按下按钮 3、2、3、0、1、2、0 后包装机的状态

一种特殊情况是，因为筐的容量是有限的，当筐已经满了，但仍然有某条轨道的按钮被按下时，系统应强制启动 0 号键，先从筐里抓出一件物品，再将对应轨道的物品推落。此外，如果轨道已经空了，再按对应的按钮不会发生任何事；同样的，如果筐是空的，按 0 号按钮也不会发生任何事。

现给定一系列按钮操作，请你依次列出流水线上的物品。

输入格式：

输入第一行给出 3 个正整数 N（≤100）、M（≤1000）和 Smax（≤100），分别为轨道的条数（于是轨道从 1 到 N 编号）、每条轨道初始放置的物品数量、以及筐的最大容量。随后 N 行，每行给出 M 个英文大写字母，表示每条轨道的初始物品摆放。

最后一行给出一系列数字，顺序对应被按下的按钮编号，直到 −1 标志输入结束，这个数字不要处理。数字间以空格分隔。题目保证至少会取出一件物品放在流水线上。

输出格式：

在一行中顺序输出流水线上的物品，不得有任何空格。

输入样例：

3 4 4
GPLT
PATA
OMSA
3 2 3 0 1 2 0 2 2 0 -1

输出样例：

MATA

//这道题也没什么难度就是直接模拟即可
#include<iostream>
#include<stack>
#include<queue>
using namespace std;
int main(){
    stack<char> s;
    int n,m,smax;
    cin>>n>>m>>smax;
    queue<char> q[n+1];
    char liu[n*m];
    int num=0;
    for(int i=1;i<=n;i++){
        for(int j=0;j<m;j++){
            char c;
            cin>>c;
            q[i].push(c);
        }
    }
    int t;
    cin>>t;
    while(t!=-1){
        if(t==0){
            if(s.size()==0){
                cin>>t;
                continue;
            }
            else{
                liu[num++]=s.top();
                s.pop();
            }
        }
        else{
            if(q[t].size()==0){
                cin>>t;
                continue;
            }
            else{
                if(s.size()<smax){
                    s.push(q[t].front());
                    q[t].pop();
                }
                else{
                     liu[num++]=s.top();
                    s.pop();
                    s.push(q[t].front());
                     q[t].pop();
                }
            }
        }
        cin>>t;
    }
    for(int i=0;i<num;i++){
        cout<<liu[i];
    }
}

L2-038 病毒溯源

分数 35

全屏浏览

切换布局

作者陈越

单位浙江大学

病毒容易发生变异。某种病毒可以通过突变产生若干变异的毒株，而这些变异的病毒又可能被诱发突变产生第二代变异，如此继续不断变化。

现给定一些病毒之间的变异关系，要求你找出其中最长的一条变异链。

在此假设给出的变异都是由突变引起的，不考虑复杂的基因重组变异问题 ------ 即每一种病毒都是由唯一的一种病毒突变而来，并且不存在循环变异的情况。

输入格式：

输入在第一行中给出一个正整数 N（≤104），即病毒种类的总数。于是我们将所有病毒从 0 到 N−1 进行编号。

随后 N 行，每行按以下格式描述一种病毒的变异情况：

k 变异株1 ...... 变异株k

其中 k 是该病毒产生的变异毒株的种类数，后面跟着每种变异株的编号。第 i 行对应编号为 i 的病毒（0≤i<N）。题目保证病毒源头有且仅有一个。

输出格式：

首先输出从源头开始最长变异链的长度。

在第二行中输出从源头开始最长的一条变异链，编号间以 1 个空格分隔，行首尾不得有多余空格。如果最长链不唯一，则输出最小序列。

注：我们称序列 { a1,⋯,an } 比序列 { b1,⋯,bn } "小"，如果存在 1≤k≤n 满足 ai=bi 对所有 i<k 成立，且 ak<bk。

输入样例：

输出样例：

4
0 4 9 1

#include<algorithm>
#include<iostream>
#include<vector>
using namespace std;
int n;
vector<int> v[10001];
vector<int> temp;//最终序列
vector<int> p;
int t[10001];
void dfs(int index){
    if(p.size()>temp.size()){//找到更深的，更新temp数组
        temp.clear();
        temp=p;
    }
    for(int i=0;i<v[index].size();i++){
        p.push_back(v[index][i]);
        dfs(v[index][i]);
        p.pop_back();
    }
}
int main(){
    cin>>n;
    for(int i=0;i<n;i++){
        int k;
        cin>>k;
        while(k--){
            int x;
            cin>>x;
            v[i].push_back(x);
            t[x]=1;//这是为了找到根节点
        }
        if(v[i].size()!=0){
            sort(v[i].begin(),v[i].end());//每次放完孩子都需要排序，以求得最小的编号
        }
    }
    for(int i=0;i<n;i++){
        if(t[i]==0){//找到根节点就直接开始深搜
            p.push_back(i);
            dfs(i);
            break;
        }
    }
    cout<<temp.size()<<endl;
    for(int i=0;i<temp.size();i++){
        if(i==0)
            cout<<temp[i];
        else
            cout<<" "<<temp[i];
    }
}

L2-039 清点代码库

分数 35

全屏浏览

切换布局

作者陈越

单位浙江大学

上图转自新浪微博："阿里代码库有几亿行代码，但其中有很多功能重复的代码，比如单单快排就被重写了几百遍。请设计一个程序，能够将代码库中所有功能重复的代码找出。各位大佬有啥想法，我当时就懵了，然后就挂了。。。"

这里我们把问题简化一下：首先假设两个功能模块如果接受同样的输入，总是给出同样的输出，则它们就是功能重复的；其次我们把每个模块的输出都简化为一个整数（在 int 范围内）。于是我们可以设计一系列输入，检查所有功能模块的对应输出，从而查出功能重复的代码。你的任务就是设计并实现这个简化问题的解决方案。

输入格式：

输入在第一行中给出 2 个正整数，依次为 N（≤104）和 M（≤102），对应功能模块的个数和系列测试输入的个数。

随后 N 行，每行给出一个功能模块的 M 个对应输出，数字间以空格分隔。

输出格式：

首先在第一行输出不同功能的个数 K。随后 K 行，每行给出具有这个功能的模块的个数，以及这个功能的对应输出。数字间以 1 个空格分隔，行首尾不得有多余空格。输出首先按模块个数非递增顺序，如果有并列，则按输出序列的递增序给出。

注：所谓数列 { A1, ..., AM } 比 { B1, ..., BM } 大，是指存在 1≤i<M，使得 A1=B1，...，Ai=Bi 成立，且 Ai+1>Bi+1。

输入样例：

输出样例：

4
3 35 28 74
2 -1 -1 22
1 11 66 0
1 28 74 35

//有意说一这道题也是比较简单的
//这些数据看着吓人，实际上整行读取就秒了,但其实如果位置不同也挺烦的(写完发现不需要考虑这个问题)
//这里我忽略了一个点就是可能会有负数
#include <iostream>
#include <algorithm>
#include <vector>
#include <map>
using namespace std;
map<vector<int>,int> cnt;
vector<pair<int, vector<int>>> ans;
int n, m;
int main(){
    cin>>n>>m;
    for (int i = 0; i < n; i++){
        vector<int> temp;
        for (int j = 0; j < m; j++){
            int x;
            cin>>x;
            temp.push_back(x);
        }
        cnt[temp]++;
    }
    for (auto u : cnt)
        ans.push_back({-u.second, u.first});
    //这里主要是不想写cmp函数了，默认对键是升序排序，想要降序就加了个负号
    sort(ans.begin(), ans.end());
    cout<<cnt.size()<<endl;
    for (auto u : ans){
        printf("%d", -u.first);
        for (auto v : u.second)
            cout<<" "<<v;
        cout<<endl;
    }
}

L2-040 哲哲打游戏

分数 35

全屏浏览

切换布局

作者 DAI, Longao

单位杭州百腾教育科技有限公司

哲哲是一位硬核游戏玩家。最近一款名叫《达诺达诺》的新游戏刚刚上市，哲哲自然要快速攻略游戏，守护硬核游戏玩家的一切！

为简化模型，我们不妨假设游戏有 N 个剧情点，通过游戏里不同的操作或选择可以从某个剧情点去往另外一个剧情点。此外，游戏还设置了一些存档，在某个剧情点可以将玩家的游戏进度保存在一个档位上，读取存档后可以回到剧情点，重新进行操作或者选择，到达不同的剧情点。

为了追踪硬核游戏玩家哲哲的攻略进度，你打算写一个程序来完成这个工作。假设你已经知道了游戏的全部剧情点和流程，以及哲哲的游戏操作，请你输出哲哲的游戏进度。

输入格式：

输入第一行是两个正整数 N 和 M (1≤N,M≤105)，表示总共有 N 个剧情点，哲哲有 M 个游戏操作。

接下来的 N 行，每行对应一个剧情点的发展设定。第 i 行的第一个数字是 Ki，表示剧情点 i 通过一些操作或选择能去往下面 Ki 个剧情点；接下来有 Ki 个数字，第 k 个数字表示做第 k 个操作或选择可以去往的剧情点编号。

最后有 M 行，每行第一个数字是 0、1 或 2，分别表示：

0 表示哲哲做出了某个操作或选择，后面紧接着一个数字 j，表示哲哲在当前剧情点做出了第 j 个选择。我们保证哲哲的选择永远是合法的。
1 表示哲哲进行了一次存档，后面紧接着是一个数字 j，表示存档放在了第 j 个档位上。
2 表示哲哲进行了一次读取存档的操作，后面紧接着是一个数字 j，表示读取了放在第 j 个位置的存档。

约定：所有操作或选择以及剧情点编号都从 1 号开始。存档的档位不超过 100 个，编号也从 1 开始。游戏默认从 1 号剧情点开始。总的选项数（即 ∑Ki）不超过 106。

输出格式：

对于每个 1（即存档）操作，在一行中输出存档的剧情点编号。

最后一行输出哲哲最后到达的剧情点编号。

输入样例：

输出样例：

样例解释：

简单给出样例中经过的剧情点顺序：

1 -> 4 -> 3 -> 7 -> 8 -> 3 -> 5 -> 9 -> 10。

档位 1 开始存的是 1 号剧情点；档位 2 存的是 3 号剧情点；档位 1 后来又存了 9 号剧情点。

#include<iostream>
#include<vector>
using namespace std;
vector<int> a[100001];
int cundang[105];
int main(){
    int n, m;
    cin >> n >> m;
    for(int i=1;i<=n;i++){
        int k;
        cin >> k;
        for(int j=1;j<=k;j++){
            int x;
            cin >> x;   
            a[i].push_back(x);
        }
    }
    int now=1;//当前存档位置
    for(int i=0;i<m;i++){
        int k;
        cin >> k;
        if(k==0){
            int kk;
            cin >> kk;
            now = a[now][kk-1];//表示从当前存档前往下一个
        }
        else if(k==1){
            int kk;
            cin >> kk;
            cundang[kk] = now;
            cout << now << "\n";
        }
        else if(k==2){
            int kk;
            cin >> kk;
            now = cundang[kk];
        }
    }
    cout << now;
    return 0; 
}

L2-041 插松枝

分数 25

全屏浏览

切换布局

作者陈越

单位浙江大学

人造松枝加工场的工人需要将各种尺寸的塑料松针插到松枝干上，做成大大小小的松枝。他们的工作流程（并不）是这样的：

每人手边有一只小盒子，初始状态为空。
每人面前有用不完的松枝干和一个推送器，每次推送一片随机型号的松针片。
工人首先捡起一根空的松枝干，从小盒子里摸出最上面的一片松针 ------ 如果小盒子是空的，就从推送器上取一片松针。将这片松针插到枝干的最下面。
工人在插后面的松针时，需要保证，每一步插到一根非空松枝干上的松针片，不能比前一步插上的松针片大。如果小盒子中最上面的松针满足要求，就取之插好；否则去推送器上取一片。如果推送器上拿到的仍然不满足要求，就把拿到的这片堆放到小盒子里，继续去推送器上取下一片。注意这里假设小盒子里的松针片是按放入的顺序堆叠起来的，工人每次只能取出最上面（即最后放入）的一片。
当下列三种情况之一发生时，工人会结束手里的松枝制作，开始做下一个：

（1）小盒子已经满了，但推送器上取到的松针仍然不满足要求。此时将手中的松枝放到成品篮里，推送器上取到的松针压回推送器，开始下一根松枝的制作。

（2）小盒子中最上面的松针不满足要求，但推送器上已经没有松针了。此时将手中的松枝放到成品篮里，开始下一根松枝的制作。

（3）手中的松枝干上已经插满了松针，将之放到成品篮里，开始下一根松枝的制作。

现在给定推送器上顺序传过来的 N 片松针的大小，以及小盒子和松枝的容量，请你编写程序自动列出每根成品松枝的信息。

输入格式：

输入在第一行中给出 3 个正整数：N（≤103），为推送器上松针片的数量；M（≤20）为小盒子能存放的松针片的最大数量；K（≤5）为一根松枝干上能插的松针片的最大数量。

随后一行给出 N 个不超过 100 的正整数，为推送器上顺序推出的松针片的大小。

输出格式：

每支松枝成品的信息占一行，顺序给出自底向上每片松针的大小。数字间以 1 个空格分隔，行首尾不得有多余空格。

输入样例：

8 3 4
20 25 15 18 20 18 8 5

输出样例：

20 15
20 18 18 8
25 5

//这个题目实际上不难
//额小盒子是栈，推送器是队列，成品蓝是数组
//直接模拟就好
#include<iostream>
#include<stack>
#include<queue>
#include<vector>
using namespace std;
int main(){
    int n,m,k;
    queue<int> q;
    stack<int> s;
    cin>>n>>m>>k;
    for(int i=0;i<n;i++){
        int x;
        cin>>x;
        q.push(x);
    }
    //因为我们不知道可能有多少个松枝，只能一直做
    while(1){
        vector<int> v;
        bool flag = 0;
        while(1){
            if(v.size()==0){
                if(s.size()!=0){
                    v.push_back(s.top());
                    s.pop();
                }
                else if(q.size()!=0){
                    v.push_back(q.front());
                    q.pop();
                }
                else{
                    break;//要是两个都空了那还做个der
                }
            }
            else{
                if(s.size()!=0&&s.top()<=v.back()){
                    v.push_back(s.top());
                    s.pop();
                }
                else{
                    while(q.size()!=0&&s.size()<=m){
                        int t=q.front();
                        if(t<=v.back()){
                            q.pop();
                            v.push_back(t);
                            break;
                        }
                        else{
                            if(s.size()==m){
                                flag=1;
                                break;
                            }
                            else{
                                s.push(t);
                                q.pop();
                            }
                        }
                    }
                    if(q.size()==0&&s.size()==0||q.size()==0&&s.top()>v.back()){
                        break;
                    }
                }
            }
            if(flag==1||v.size()==k)
                break;
        }
        for(int i=0;i<v.size();i++){
            if(i!=v.size()-1){
                cout<<v[i]<<" ";
            }
            else
                cout<<v[i]<<endl;
        }
        if(q.size()==0&&s.size()==0)
            break;
    }
}

L2-042 老板的作息表

分数 25

全屏浏览

切换布局

作者陈越

单位浙江大学

新浪微博上有人发了某老板的作息时间表，表示其每天 4:30 就起床了。但立刻有眼尖的网友问：这时间表不完整啊，早上九点到下午一点干啥了？

本题就请你编写程序，检查任意一张时间表，找出其中没写出来的时间段。

输入格式：

输入第一行给出一个正整数 N，为作息表上列出的时间段的个数。随后 N 行，每行给出一个时间段，格式为：

hh:mm:ss - hh:mm:ss

其中 hh、mm、ss 分别是两位数表示的小时、分钟、秒。第一个时间是开始时间，第二个是结束时间。题目保证所有时间都在一天之内（即从 00:00:00 到 23:59:59）；每个区间间隔至少 1 秒；并且任意两个给出的时间区间最多只在一个端点有重合，没有区间重叠的情况。

输出格式：

按照时间顺序列出时间表中没有出现的区间，每个区间占一行，格式与输入相同。题目保证至少存在一个区间需要输出。

输入样例：

8
13:00:00 - 18:00:00
00:00:00 - 01:00:05
08:00:00 - 09:00:00
07:10:59 - 08:00:00
01:00:05 - 04:30:00
06:30:00 - 07:10:58
05:30:00 - 06:30:00
18:00:00 - 19:00:00

输出样例：

04:30:00 - 05:30:00
07:10:58 - 07:10:59
09:00:00 - 13:00:00
19:00:00 - 23:59:59

#include<iostream>
#include<algorithm>
using namespace std;
int main(){
    int n;
    cin>>n;
    getchar();
    string s[n];
    for(int i=0;i<n;i++)
    getline(cin,s[i]);
    sort(s,s+n);
    string min="00:00:00";
    string max="23:59:59";
    if(s[0].substr(0,8)>min)
        cout<<min<<" - "<<s[0].substr(0,8)<<endl;
    string t=s[0].substr(11,s[0].length());
    for(int i=1;i<n;i++){
        if(t<s[i].substr(0,8)){
            cout<<t<<" - "<<s[i].substr(0,8)<<endl;
            t=s[i].substr(11,s[0].length());
        }
        else if(t>=s[i].substr(0,8)&&t<=s[i].substr(11,s[0].length()))
            t=s[i].substr(11,s[0].length());
        else if(t>s[i].substr(11,s[0].length()))
            continue;
    }
    if(t<max)
        cout<<t<<" - "<<max;
}

L2-043 龙龙送外卖

分数 35

全屏浏览

切换布局

作者 DAI, Longao

单位杭州百腾教育科技有限公司

龙龙是"饱了呀"外卖软件的注册骑手，负责送帕特小区的外卖。帕特小区的构造非常特别，都是双向道路且没有构成环 ------ 你可以简单地认为小区的路构成了一棵树，根结点是外卖站，树上的结点就是要送餐的地址。

每到中午 12 点，帕特小区就进入了点餐高峰。一开始，只有一两个地方点外卖，龙龙简单就送好了；但随着大数据的分析，龙龙被派了更多的单子，也就送得越来越累......

看着一大堆订单，龙龙想知道，从外卖站出发，访问所有点了外卖的地方至少一次（这样才能把外卖送到）所需的最短路程的距离到底是多少？每次新增一个点外卖的地址，他就想估算一遍整体工作量，这样他就可以搞明白新增一个地址给他带来了多少负担。

输入格式:

输入第一行是两个数 N 和 M (2≤N≤105, 1≤M≤105)，分别对应树上节点的个数（包括外卖站），以及新增的送餐地址的个数。

接下来首先是一行 N 个数，第 i 个数表示第 i 个点的双亲节点的编号。节点编号从 1 到 N，外卖站的双亲编号定义为 −1。

接下来有 M 行，每行给出一个新增的送餐地点的编号 Xi。保证送餐地点中不会有外卖站，但地点有可能会重复。

为了方便计算，我们可以假设龙龙一开始一个地址的外卖都不用送，两个相邻的地点之间的路径长度统一设为 1，且从外卖站出发可以访问到所有地点。

注意：所有送餐地址可以按任意顺序访问，且完成送餐后无需返回外卖站。

输出格式:

对于每个新增的地点，在一行内输出题目需要求的最短路程的距离。

输入样例:

7 4
-1 1 1 1 2 2 3
5
6
2
4

输出样例:

2
4
4
6

//由于节点只会有一个双亲，我们直接用并查集的思维秒了
//可以用并查集来判断哪些点在同一条线路上，但好像也不太行
//到后来发现其实最短距离就是所有边*2-最大深度即可
//这里必须要用记忆搜索法，不然不好计算长度
//还需要使用剪枝的思维，否则容易超时
#include<iostream>
const int N=100001;
int parent[N];
int Dist=0;
bool visit[N]={false};
int dp[N]={0};
int root;
using namespace std;
void dfs1(int start,int dist){
    if(start==root||visit[start]==true){
        Dist=Dist+dist;
        return ;
    }
    visit[start]=true;
    dfs1(parent[start],dist+2);
}
//这个是用来找最大深度的,额也不是就是计算root1到根的深度
int dfs2(int root1){
    if(dp[root1]!=0||root1==root)
        return dp[root1];
    dp[root1]=dfs2(parent[root1])+1;
    return dp[root1];
}
int main(){
    int n,m;
    cin>>n>>m;
    for(int i=1;i<=n;i++){
        parent[i]=i;
    }
    for(int i=1;i<=n;i++){
        int x;
        cin>>x;
        parent[i]=x;
        if(x==-1)
            root=i;//找到根
    }
    int distamax=0;
    for(int j=0;j<m;j++){
        int x;
        cin>>x;
        dfs1(x,0);
        distamax=max(distamax,dfs2(x));
        cout<<Dist-distamax<<endl;
    }
}

L2-044 大众情人

分数 35

全屏浏览

切换布局

作者陈越

单位浙江大学

人与人之间总有一点距离感。我们假定两个人之间的亲密程度跟他们之间的距离感成反比，并且距离感是单向的。例如小蓝对小红患了单相思，从小蓝的眼中看去，他和小红之间的距离为 1，只差一层窗户纸；但在小红的眼里，她和小蓝之间的距离为 108000，差了十万八千里...... 另外，我们进一步假定，距离感在认识的人之间是可传递的。例如小绿觉得自己跟小蓝之间的距离为 2，则即使小绿并不直接认识小红，我们也默认小绿早晚会认识小红，并且因为跟小蓝很亲近的关系，小绿会觉得自己跟小红之间的距离为 1+2=3。当然这带来一个问题，如果小绿本来也认识小红，或者他通过其他人也能认识小红，但通过不同渠道推导出来的距离感不一样，该怎么算呢？我们在这里做个简单定义，就将小绿对小红的距离感定义为所有推导出来的距离感的最小值。

一个人的异性缘不是由最喜欢他/她的那个异性决定的，而是由对他/她最无感的那个异性决定的。我们记一个人 i 在一个异性 j 眼中的距离感为 Dij；将 i 的"异性缘"定义为 1/maxj∈S(i){Dij}，其中 S(i) 是相对于 i 的所有异性的集合。那么"大众情人"就是异性缘最好（值最大）的那个人。

本题就请你从给定的一批人与人之间的距离感中分别找出两个性别中的"大众情人"。

输入格式：

输入在第一行中给出一个正整数 N（≤500），为总人数。于是我们默认所有人从 1 到 N 编号。

随后 N 行，第 i 行描述了编号为 i 的人与其他人的关系，格式为：

性别 K 朋友1:距离1 朋友2:距离2 ...... 朋友K:距离K

其中 性别 是这个人的性别，F 表示女性，M 表示男性；K（<N 的非负整数）为这个人直接认识的朋友数；随后给出的是这 K 个朋友的编号、以及这个人对该朋友的距离感。距离感是不超过 106 的正整数。

题目保证给出的关系中一定两种性别的人都有，不会出现重复给出的关系，并且每个人的朋友中都不包含自己。

输出格式：

第一行给出自身为女性的"大众情人"的编号，第二行给出自身为男性的"大众情人"的编号。如果存在并列，则按编号递增的顺序输出所有。数字间以一个空格分隔，行首尾不得有多余空格。

输入样例：

6
F 1 4:1
F 2 1:3 4:10
F 2 4:2 2:2
M 2 5:1 3:2
M 2 2:2 6:2
M 2 3:1 2:5

输出样例：

2 3
4

#include <bits/stdc++.h>
using namespace std;
struct node{
    char sex;
    int idx, num;
} a[510], b[510], c[510];
int e[510][510];
int cnt1, cnt2;
bool cmp(struct node x,struct node y){
    if (x.num == y.num)
        return x.idx < y.idx;
    return x.num < y.num;
}
int main(){
    int n;
    cin >> n;
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= n; j++)
            if (i != j)
                e[i][j] =1000000000;
            else
                e[i][j] = 0;
    for (int i = 1; i <= n; i++){
        getchar();
        int m;
        scanf("%c%d", &a[i].sex, &m);
        a[i].idx = i;
        for (int j = 1; j <= m; j++){
            int x, y;
            scanf("%d:%d", &x, &y);
            e[i][x] = y;
        }
    }
    for (int k = 1; k <= n; k++)
        for (int i = 1; i <= n; i++)
            for (int j = 1; j <= n; j++)
                if (e[i][j] > e[i][k] + e[k][j])
                    e[i][j] = e[i][k] + e[k][j];
    for (int i = 1; i <= n; i++){
        int res = 0;
        int j;
        for (j = 1; j <= n; j++){
            if (a[i].sex != a[j].sex)
                res = max(res, e[j][i]);
        }
        if (a[i].sex == 'F'){
            b[++cnt1].num = res;
            b[cnt1].idx = a[i].idx;
        }
        else{
            c[++cnt2].num = res;
            c[cnt2].idx = a[i].idx;
        }
    }
    sort(b + 1, b + 1 + cnt1, cmp);
    sort(c + 1, c + 1 + cnt2, cmp);
    int i = 1;
    while (b[i].num == b[1].num){
        if (i!=1)
            cout << " ";
        cout << b[i].idx;
        i++;
    }
    i = 1;
    cout << endl;
    while (c[i].num == c[1].num){
        if (i!=1)
            cout << " ";
        cout << c[i].idx;
        i++;
    }
}