红黑树(数据结构篇)

数据结构之红黑树

红黑树(RB-tree)

概念：

红黑树 是AVL树的变种，它是每一个节点或者着成红色，或者着成黑色的一棵二叉查找树。
对红黑树的操作在最坏情形下花费O(logN)时间，它的插入操作使用的是非递归形式实现
红黑树的高度最多是2log(N+1)

特性：

红黑树是具有着色性质 的二叉查找树 ，也就意味着树的节点值是有序的 ，且每个节点只可能是红色或者黑色
红黑树的根是黑色的
如果一个节点是红色的 ，那么它的子节点必须是黑色的
从一个节点到一个空指针 的每一条路径必须包含相同数目的黑色节点

自顶向下插入操作：

如果使用自底向上插入的话还需要进行逐步递归是他们保证满足红黑树特性，效率就降低了。
令X为新插入节点(在下面的第三操作中为当前节点)，P为X的父节点，G为P的父节点(也就是X的祖父节点)，GP为G的父节点(也就是P的祖父节点，X的曾祖父节点)
因为红黑树是一颗二叉查找树，因此在插入时需要查找要插入的值的正确位置 ，在这个查找路径中 ，如果遇到节点(X)为黑色而子节点全部为红色 ，我们就进行翻转操作，也就是将该节点(X)着成红色，子节点全部着成黑色 。翻转后:
如果翻转后发现P和X节点都是红色 就需要根据树的结构进行旋转操作
1. 如果X，P，G形成"一字形" ，则对P的父节点G (也就是X的祖父节点)与P进行 单旋转，并将新根也就是P着成黑色，新根的子节点都着成红色。
2. 如果X，P，G形成"之字形" ，则对G与X节点 进行双旋转，并将新根着成黑色(也就是X节点) ，然后将新根的子节点着成红色
如果该节点(X)是黑色则继续将X下降 ，直到找到红色节点继续翻转 ，或者找到指定插入位置 ，找到指定位置也就是当前节点位置X就进行插入，新节点也是红色，需要重新判断其父节点是否为红色，为红色又需要进行翻转操作来调整。

自顶向下删除操作

自顶向下删除也需要保证红黑树的性质，插入是插入一片红色的叶子节点，那么反过来我们删除一个红色叶子节点就不会破坏红黑树性质 ，自顶向下插入的翻转操作是将红色节点减少，并将红色节点上浮 ，因为删除是插入的逆过程，因此删除的翻转操作就是要将树中的红色节点增多，并将红色节点下沉，这样我们删除红色叶子节点的概率更大，并且不会破坏红黑树性质
删除操作一共有5种情况需要解决
1. 要删除节点cur跟其兄弟节点s原本颜色为黑色 ，父亲节点p为红色
2. s的两个儿子都是红色 ，这样双旋转和单旋转都可以，这里优先选择ps单选转调整，情况1-case4
3. s的左儿子为红色 ，需要ps.l双旋转调整(s.l为s的左儿子)，情况2-case1
4. s的右儿子为红色 ，需要ps单旋转调整，情况3-case2
5. s有两个黑色儿子 ，直接cur,p,s颜色翻转操作调整，情况4-case3
6. p和cur为黑色 ，s为红色 ，需要交换sp节点的颜色，并且sp单旋转调整，情况5-case5
7. cur为红色 ，可以继续将cur下降，也就是当前cur指向原本cur的子节点，如果为红色继续下降，如果为黑色就判断是否需要操作
tomove指向要删除节点也就是目标节点，而p指向真正要删除的叶子节点，cur则while循环完后则是指向nil节点，因为将tomove标记完，就进行cur和p就查找tomove右子树的最小值节点进行删除，而while循环终止条件为cur==nil情况，因此p指向真正要删除的节点
找到tomove和p后，将tomove的data等于p的data，将p删除，因为p为叶子节点，将p的父节点指向nil。

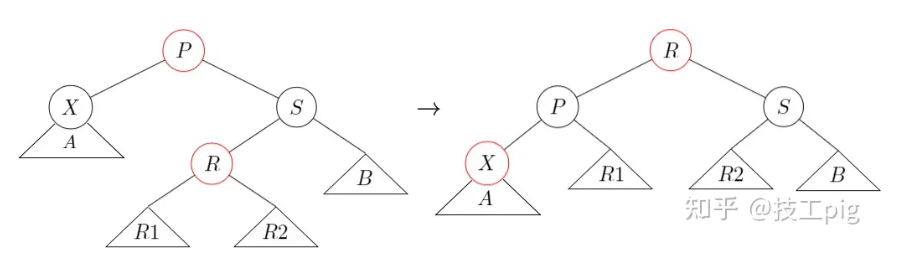情况2-case1

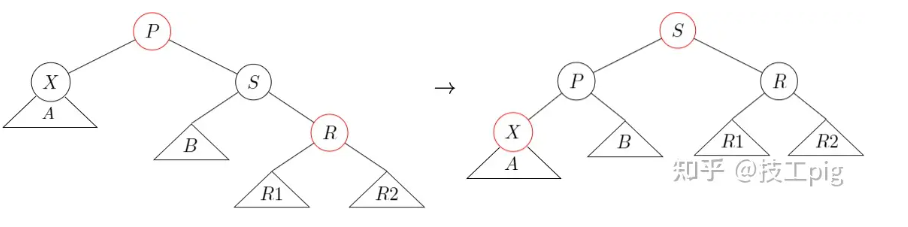情况3-case2

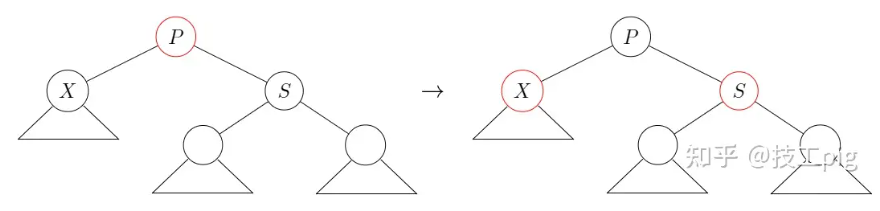情况4-case3

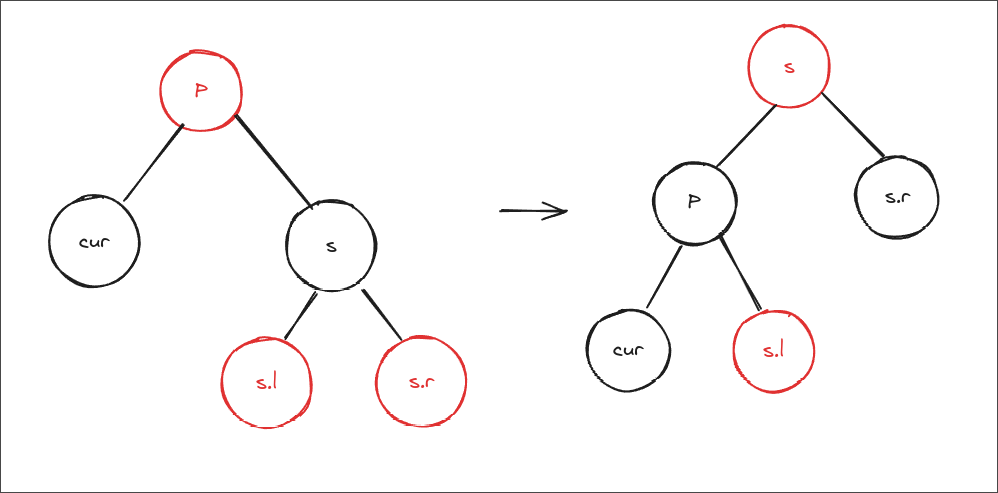情况1-case4

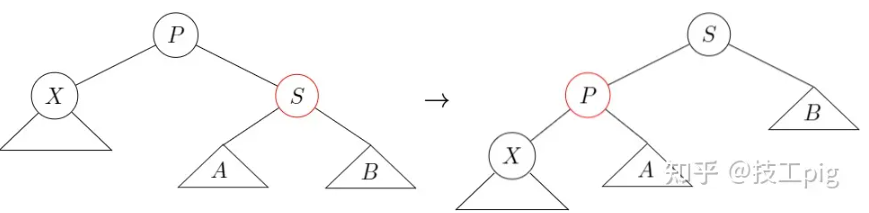情况5-case5

计算红黑树层数：

需要对log2(树中总共节点数+1)向上取整

代码：

c++ 复制代码

int Height(const int count){
    return std::ceil(std::log2(count+1));
}

代码实现：

cpp 复制代码

#include <iostream>
#include <queue>
#include <math.h>
#include <limits.h>
using namespace std;

typedef enum {red,black} colortype;

struct RBNode{
    int data;
    RBNode *left,*right,*parent;
    colortype color;   //颜色
    RBNode(const int val,RBNode* l,RBNode* r,RBNode* p,colortype c=red):data(val),
                                                                        left(l),right(r),parent(p),color(c){};
};

class RBtree{
public:
    RBtree(){
        nil=new RBNode(INT_MAX, nullptr, nullptr, nullptr,black);
        root= nullptr;
        t=new RBNode(INT_MIN,nil,nil,nil,black);
        size=0;
    }

    ~RBtree(){
        clear();
        delete t;
        delete nil;
    };
    void insert(const int val);      //插入操作
    void del(const int val);       //删除操作
    RBNode* find(const int val);   //查找操作
    void print();     //打印操作,层序遍历
    //清空操作
    void clear(){
        clear(root);
        root= nullptr;
        t->right=nil;
        size=0;
    }

protected:
    void overturnred(const int val,RBNode* &cur);    //翻转操作,将当前节点变成红色，子节点变成黑色
    void overturnblack(int val,RBNode* &cur);   //翻转操作，将当前节点变成黑色，子节点变成红色
    RBNode* SingleRotatewithleft(RBNode* &k1);
    RBNode* SingleRotatewithright(RBNode* &k1);
    RBNode* Rotate(const int val,RBNode* &k1){
        if(val<k1->data){
            return k1->left=val<k1->left->data? SingleRotatewithleft(k1->left): SingleRotatewithright(k1->left);
        }else{
            return k1->right=val<k1->right->data? SingleRotatewithleft(k1->right): SingleRotatewithright(k1->right);
        }
    }
    void clear(RBNode* &rt);
    // 计算红黑树层数
    int Height(int nodeCount) {
        // 红黑树的层数为 log2(nodeCount+1)
        return (int)std::ceil(std::log2(nodeCount+1));
    }
private:
    RBNode* root;
    RBNode* nil;   //空节点，color为黑色
    RBNode* t;  //根标记，用于删除操作的便捷
    int size;
};

RBNode* RBtree::SingleRotatewithleft(RBNode *&k1) {
    RBNode* k2;
    k2=k1->left;
    k1->left=k2->right;
    k2->right=k1;
    return k2;
}

RBNode* RBtree::SingleRotatewithright(RBNode *&k1) {
    RBNode* k2;
    k2=k1->right;
    k1->right=k2->left;
    k2->left=k1;
    return k2;
}

//翻转操作
void RBtree::overturnred(const int val,RBNode* &cur) {
    cur->color=red;
    cur->left->color=cur->right->color=black;
    RBNode* p=cur->parent;
    if(p->color==red){
        RBNode* g=p->parent;
        g->color=red;
        if((val<g->data)!=(val<p->data)){     //双旋转
            p= Rotate(val,g);
        }
        cur= Rotate(val,g->parent);
        cur->color=black;
    }
    root->color=black;
}


//插入操作
void RBtree::insert(const int val) {
    if(root== nullptr){
        root=new RBNode(val,nil,nil, t,black);
        t->right=root;
        size++;
        return;
    }
    RBNode *cur,*p;
    cur=p=root;
    while (cur!=nil){
        p=cur;
        if(cur->left->color==red&&cur->right->color==red){
            overturnred(val,cur);
        }
        cur=val<p->data?p->left:p->right;
    }
    if(cur!=nil){
        return;
    }
    cur=new RBNode(val, nil, nil, p);
    if(val<p->data){
        p->left=cur;
    }else{
        p->right=cur;
    }
    overturnred(val,cur);
    size++;
}

void RBtree::overturnblack(int val, RBNode *&cur) {
    cur->color=red;
    RBNode* p=cur->parent;
    RBNode* s=val<p->data?p->left:p->right;
    //case4:要删除节点cur跟其兄弟节点s原本颜色为黑色，父亲节点p为红色，s的两个儿子都是红色，这样双旋转和单旋转都可以，这里优先选择ps单选转
    //case2:要删除节点cur跟其兄弟节点s原本颜色为黑色，父亲节点p为红色，s的右儿子为红色情况，需要ps单旋转调整
    if(s->right->color==red){
        val=s->right->data;
    }
    //case1:要删除节点cur跟其兄弟节点s原本颜色为黑色，父亲节点p为红色，s的左儿子为红色的情况,需要ps.l双旋转调整
    else if(s->left->color==red){
        val=s->left->data;
    }
        //case3:要删除节点cur跟其兄弟节点s原本颜色为黑色，父亲节点p为红色，s有两个黑儿子(nil节点也是黑色),直接将颜色翻转即可
    else{
        //翻转操作
        if(s!=nil){
            s->color=red;
        }
        p->color=black;
        return;
    }
    if((val<s->data)!=(val<p->data)){
        Rotate(val,p);
    }
    RBNode* g=p->parent;
    Rotate(val,g);
    //将调整完的cur的新祖父也就是s或者s的左儿子变成红色，也就是删除完cur后将颜色调整到之前cur在翻转前的情况
    g->color=red;
    g->left->color=g->right->color=black;
}


void RBtree::del(const int val) {
    RBNode* tomove=nil;  //找到删除节点
    RBNode *g,*p,*s,*cur;
    g=p=t,s=t->left,cur=root;
    while (cur!=nil){
        //翻转颜色
        if(cur->left->color==black&&cur->right->color==black){
            overturnblack(val,cur);
        }else{
            g=p;p=cur;
            if(val<p->data){
                cur=p->left,s=p->right;
            }else{
                tomove=cur,cur=p->right,s=p->left;
            }
            //case5:此时肯定p和cur都为黑色，因为如果p为红色早就翻转了，s肯定是红色，将s变成黑色，p变为红色，sp单旋转调整
            if(cur->color==black){
                s->color=black;
                p->color=red;
                //单旋转完，cur新祖父变为s,将s重新更改
                g= Rotate(val,g);
                s=val<p->data?p->left:p->right;
                //调整完该情况就重新检查上述操作
                continue;
            }
            //else，cur一定为红色，则可以直接继续将cur继续下降
        }
        g=p;p=cur;
        if(val<p->data){
            cur=p->left,s=p->right;
        }else{
            tomove=cur,cur=p->right,s=p->left;
        }
    }
    root->color=black;   //保证红黑树性质2不被破坏，也就是根一定为黑色

    //判断是否找到真正要删除的节点，如果找不到就退出
    if(tomove==nil&&tomove->data!=val){
        cout<<"未找到要删除对应值的节点";
        return;
    }

    //tomove是要删除的节点，而p指向的是真正要删除的节点
    tomove->data=p->data;
    if(g->left==p) g->left=nil;
    else g->right=nil;
    delete p;
    size--;
}

RBNode* RBtree::find(const int val) {
    if(root!= nullptr){
        RBNode* cur=root;
        while (cur!=nil){
            if(cur->data==val) return cur;
            cur=val<cur->data?cur->left:cur->right;
        }
        if(cur==nil){
            cout<<"树中没有指定值节点"<<endl;
        }
    }
    return root;
}

void RBtree::print() {
    if(root== nullptr){
        cout<<"树为空"<<endl;
        return;
    }
    queue<RBNode*>q;
    q.push(root);
    int cnt=1;
    int ans=0;
    int h= Height(size);
    while (!q.empty()){
        if(ans==h+1) break;
        RBNode* cur=q.front();
        q.pop();
        if(cur== nullptr){
            cout<<"null"<<" ";
            continue;
        }
        q.push(cur->left);
        q.push(cur->right);
        if(cur->color==red){
            cout<<"\033[31m"<<cur->data<<"\033[0m"<<" ";
        }else if(cur==nil) cout<<"nil"<<" ";
        else cout<<cur->data<<" ";
        if(cnt==pow(2,ans)){
            cout<<endl;
            cnt=0,ans++;
        }
        cnt++;
    }
    return;
}


void RBtree::clear(RBNode* &rt) {
    if(rt!=nil){
        clear(rt->left);
        clear(rt->right);
        delete rt;
        rt=nil;
    }
    return;
}

int main() {
    RBtree rBtree;
    rBtree.insert(30);
    rBtree.insert(15);
    rBtree.insert(65);
    rBtree.insert(10);
    rBtree.insert(20);
    rBtree.insert(5);
    rBtree.insert(60);
    rBtree.insert(70);
    rBtree.insert(50);
    rBtree.insert(64);
    rBtree.insert(66);
    rBtree.insert(85);
    rBtree.insert(40);
    rBtree.insert(55);
    rBtree.insert(63);
    rBtree.insert(80);
    rBtree.insert(90);
    rBtree.insert(45);
    rBtree.del(65);
    rBtree.del(50);
    rBtree.del(30);
    rBtree.print();
    return 0;
}

尾言

完整版笔记也就是数据结构与算法专栏完整版可到我的博客进行查看，或者在github库中自取(包含源代码)

博客1： codebooks.xyz

博客2：moonfordream.github.io

github项目地址：Data-Structure-and-Algorithms