【数据结构初阶】--排序(四)：归并排序

草莓熊Lotso2025-08-07 9:23

🔥个人主页：@草莓熊Lotso

🎬作者简介：C++研发方向学习者

📖个人专栏：************************************************************************************************************************************************************************************************************************************************************《C语言》《数据结构与算法》《C语言刷题集》《Leetcode刷题指南》****************************************************************************************************************************************************************************************************************************************************************

⭐️人生格言：生活是默默的坚持，毅力是永久的享受。

前言：在前面的学习中，我们实现了直接插入排序，希尔排序，直接选择排序，堆排序，冒泡排序，快速排序。我们常见的几种排序算法也差不过都学完了。那么我们这篇博客就继续接着上一篇博客实现完的排序往后写，来讲讲归并排序，还是和之前一样，我们先分部分来讲解，特别声明一下，博客中的排序都是以升序为例的。

目录

一.递归实现归并排序

具体过程：

代码实现：

时间复杂度：

二.非递归实现归并排序

具体过程：

代码实现：

三.归并排序的性能测试

代码演示：

一.递归实现归并排序

归并排序（MERGE-SORT）是建立在归并操作上的⼀种有效的排序算法,该算法是采用分治法（Divide and Conquer）的⼀个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成⼀个有序表，称为二路归并。

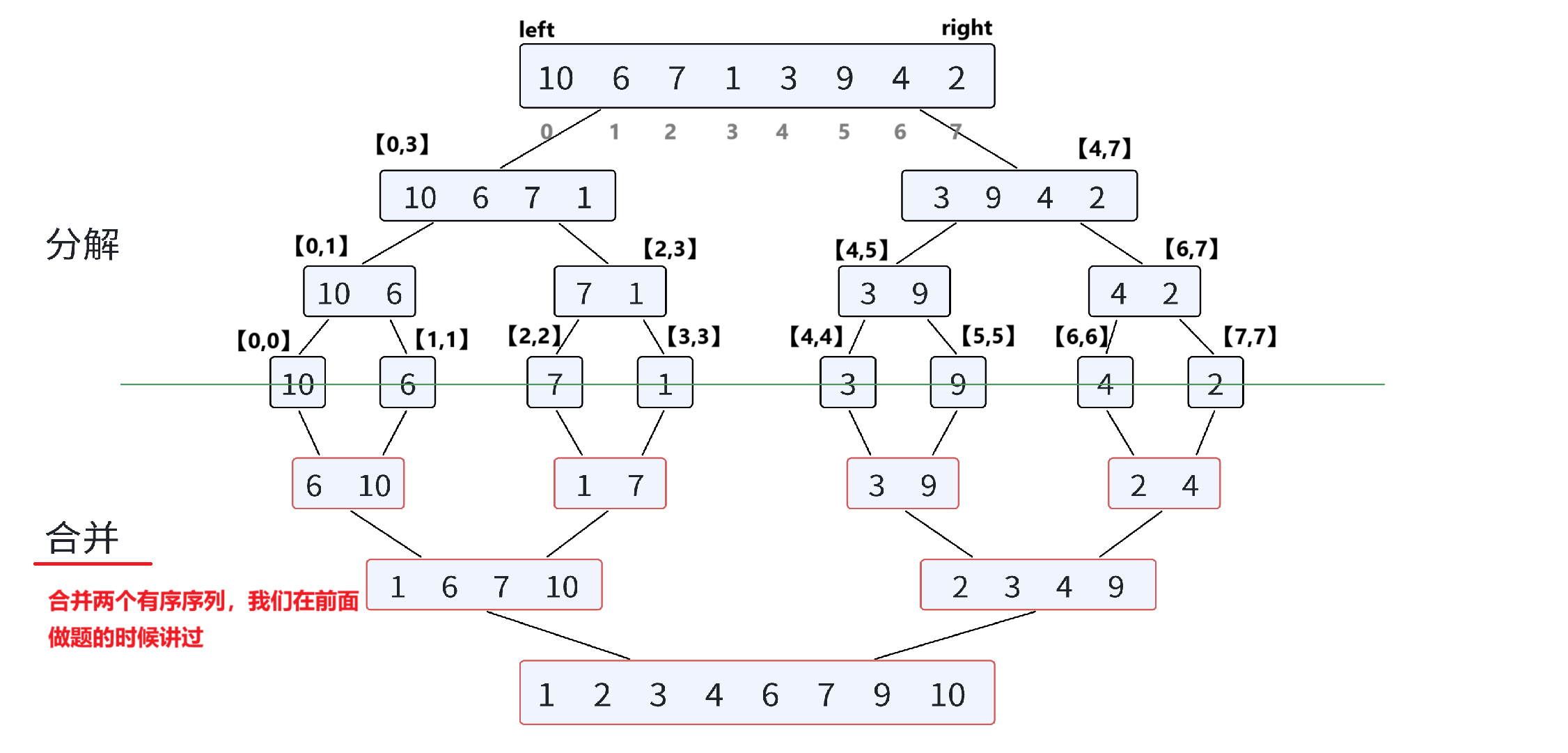--我们着重讲一下分治的思想。合并操作需要注意的地方，大家看看后面代码的重点提示就行了

将待排序的数组不断分割成更小的子数组，直到每个子数组只包含一个元素。

具体过程：

  • 找到数组的中间位置，一般是通过 mid = left + (right - left) / 2 来计算，left 和 right 分别表示当前数组范围的起始和结束索引。
  • 然后递归地对数组的左半部分（索引范围从 left 到 mid）和右半部分（索引范围从 mid + 1 到 right）进行同样的分割操作，直到子数组的长度为 1。例如，对于数组 [5, 3, 8, 6, 2]，第一次分割得到 [5, 3] 和 [8, 6, 2]，然后继续递归分割这两个子数组，直到每个子数组都只有一个元素，即 [5]、[3]、[8]、[6]、[2] 。

代码实现：

cpp 复制代码 
void _MergeSort(int* arr, int left, int right, int* tmp)
{
	if (left >= right)
	{
		return;
	}
	
	//分解
	//[left,mid][mid+1,right]
	int mid = left + (right-left) / 2;  
	_MergeSort(arr, left, mid, tmp);
	_MergeSort(arr, mid+1, right, tmp);

	//合并
	int begin1 = left, end1 = mid;
	int begin2 = mid + 1, end2 = right;
	int index = left;//一定是left而不是0，不然会受到影响

	while (begin1 <= end1 && begin2 <= end2)
	{
		if (arr[begin1] < arr[begin2])
		{
			tmp[index++] = arr[begin1++];
		}
		else {
			tmp[index++] = arr[begin2++];
		}
	}

	//有一个结束了，另外一个还没结束
	while (begin1 <= end1)
	{
		tmp[index++] = arr[begin1++];
	}
	while (begin2 <= end2)
	{
		tmp[index++] = arr[begin2++];
	}

	//把数据拷贝回去
	for (int i = left; i <= right; i++)
	{
		arr[i] = tmp[i];
	}
}

//归并排序--主函数里面不递归，所以可以先不传left和right
void MergeSort(int* arr, int n)
{
	//开辟一个新数组
	int* tmp = (int*)malloc(sizeof(int) * n);
	if (tmp == NULL)
	{
		perror("malloc fail!");
		exit(1);
	}
	_MergeSort(arr, 0, n - 1, tmp);
	free(tmp);
}

重点提示：

test.c:

cpp 复制代码 
#include"Sort.h"

void PrintArr(int* arr, int n)
{
	for (int i = 0; i < n; i++)
	{
		printf("%d ", arr[i]);
	}
	printf("\n");
}

void test1()
{
	int a[] = { 5, 3, 9, 6, 2, 4, 7, 1, 8 };
	int size = sizeof(a) / sizeof(a[0]);
	printf("排序前:");
	PrintArr(a, size);

	//归并排序
	MergeSort(a, size);

	printf("排序后:");
	PrintArr(a, size);
}

int main()
{
	test1();
	return 0;
}

--测试完成，升序排序没有问题，退出码为0

时间复杂度：

  • O(nlogn)

--时间复杂度 = 单次递归时间复杂度 * 递归次数

二.非递归实现归并排序

非递归版本的归并排序（迭代实现），核心思想是 "自底向上" 合并子数组，无需递归，直接通过循环控制分组大小（gap），逐步完成排序。

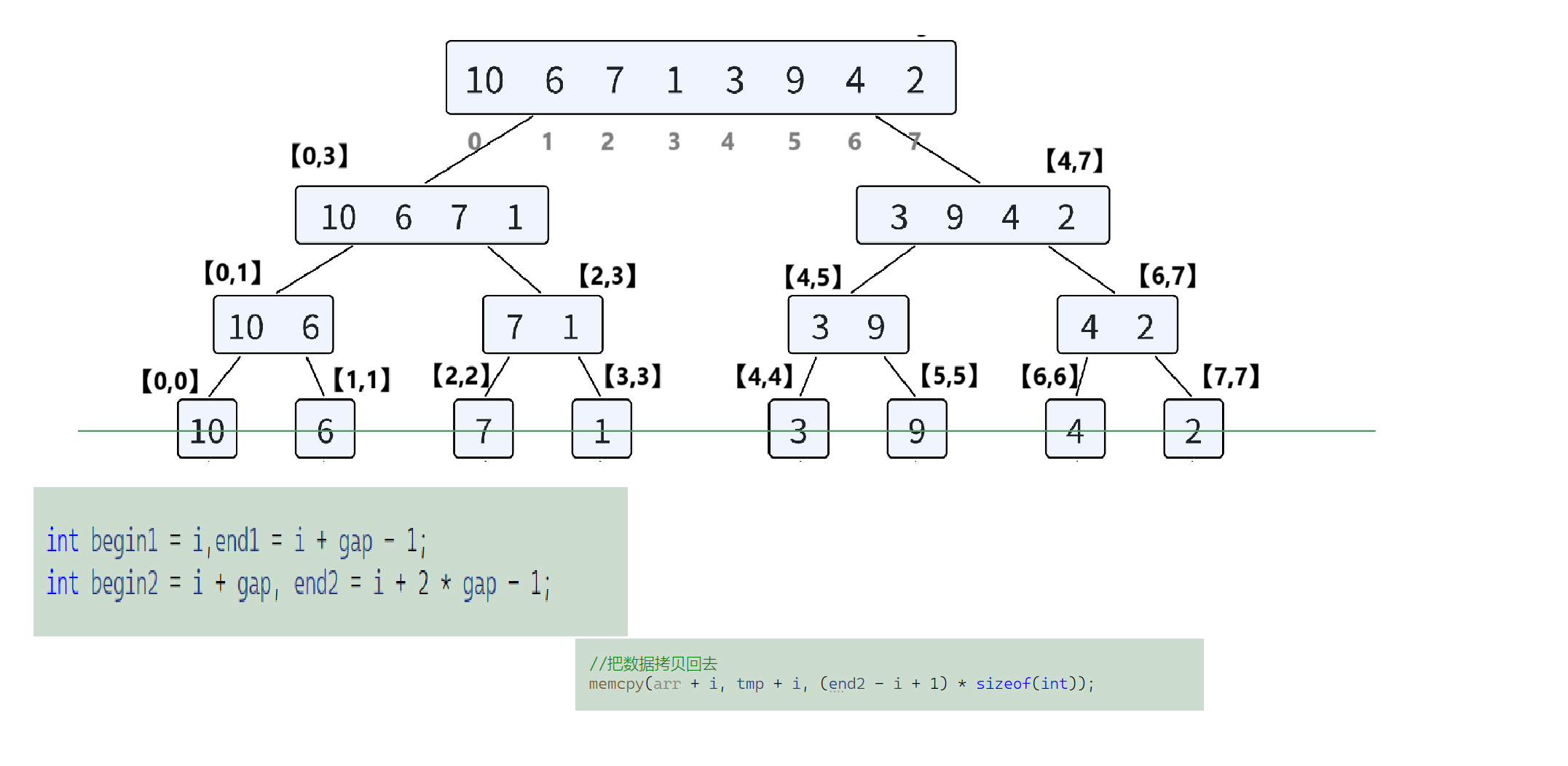
具体过程：

1. 分组合并：

  • gap 从 1 开始，每次翻倍（gap *= 2），表示当前合并的子数组长度。
  • 例如：gap=1 时，合并相邻的 1 个元素 组成的子数组（实际是单个元素，视为有序）；gap=2 时，合并相邻的 2 个元素 组成的有序子数组，以此类推。

2. 边界修正

  • 计算 end1，end2 时，需判断是否超出数组范围（n-1 是最后一个元素的索引）。
  • 若 begin2 >= n，说明第二个子数组不存在，直接跳过合并。

3. 合并操作

  • 用双指针法合并两个有序子数组到 tmp，再通过 memcpy 写回原数组。
  • 保证合并后子数组有序，逐层向上归并。

代码实现：

cpp 复制代码 
//非递归实现归并排序
void MergeSortNore(int* arr, int n)
{
	int* tmp = (int*)malloc(sizeof(int) * n);
	if (tmp == NULL)
	{
		perror("malloc fail!");
		exit(1);
	}

	int gap = 1;
	while (gap < n)
	{
		for (int i = 0; i < n; i += 2 * gap)
		{
			int begin1 = i,end1 = i + gap - 1;
			int begin2 = i + gap, end2 = i + 2 * gap - 1;
			
			if (begin2 >= n)
			{
				break;
			}
			if (end2 >= n)
			{
				end2 = n - 1;
			}
			int index = i;
			while (begin1 <= end1 && begin2 <= end2)
			{
				if (arr[begin1] < arr[begin2])
				{
					tmp[index++] = arr[begin1++];
				}
				else {
					tmp[index++] = arr[begin2++];
				}
			}
			//有一个结束了，另外一个还没结束

			while (begin1 <= end1)
			{
				tmp[index++] = arr[begin1++];
			}
			while (begin2 <= end2)
			{
				tmp[index++] = arr[begin2++];
			}

			//把数据拷贝回去
			memcpy(arr + i, tmp + i, (end2 - i + 1) * sizeof(int));
		}
		gap *= 2;
	}
	free(tmp);
}

test.c：

cpp 复制代码 
#include"Sort.h"

void PrintArr(int* arr, int n)
{
	for (int i = 0; i < n; i++)
	{
		printf("%d ", arr[i]);
	}
	printf("\n");
}

void test1()
{
	int a[] = { 5, 3, 9, 6, 2, 4, 7, 1, 8 };
	int size = sizeof(a) / sizeof(a[0]);
	printf("排序前:");
	PrintArr(a, size);

	//非递归实现归并排序
	MergeSortNore(a, size);

	printf("排序后:");
	PrintArr(a, size);
}

int main()
{
	//TestOP();
	test1();
	return 0;
}

--测试完成，升序排序没有问题，退出码为0

三.归并排序的性能测试

--我们实现完了这么多种排序，我们还是通过测试函数看看它们的性能对比吧

代码演示：

cpp 复制代码 
include"Sort.h"

void PrintArr(int* arr, int n)
{
	for (int i = 0; i < n; i++)
	{
		printf("%d ", arr[i]);
	}
	printf("\n");
}

void test1()
{
	int a[] = { 5, 3, 9, 6, 2, 4, 7, 1, 8 };
	int size = sizeof(a) / sizeof(a[0]);
	printf("排序前:");
	PrintArr(a, size);

	//直接插入排序
	//InsertSort(a, size);
	//希尔排序
	//ShellSort(a, size);
	//直接选择排序
	//SelectSort(a, size);
	//堆排序
	//HeapSort(a, size);
	//冒泡排序
	//BubbleSort(a, size);
	//快速排序
	//QuickSort(a, 0, size - 1);
	//非递归快速排序
	//QuickSortNoare(a, 0, size - 1);
	//快速排序进阶版
	//QuickSortMore(a, 0, size - 1);
	//归并排序
	//MergeSort(a, size);
	//非递归实现归并排序
	//MergeSortNore(a, size);
	//非比较排序--计数排序
	CountSort(a, size);

	printf("排序后:");
	PrintArr(a, size);
}

// 测试排序的性能对比
void TestOP()
{
	srand(time(0));
	const int N = 100000;
	int* a1 = (int*)malloc(sizeof(int) * N);
	int* a2 = (int*)malloc(sizeof(int) * N);
	int* a3 = (int*)malloc(sizeof(int) * N);
	int* a4 = (int*)malloc(sizeof(int) * N);
	int* a5 = (int*)malloc(sizeof(int) * N);
	int* a6 = (int*)malloc(sizeof(int) * N);
	int* a7 = (int*)malloc(sizeof(int) * N);
	for (int i = 0; i < N; ++i)
	{
		a1[i] = rand();
		a2[i] = a1[i];
		a3[i] = a1[i];
		a4[i] = a1[i];
		a5[i] = a1[i];
		a6[i] = a1[i];
		a7[i] = a1[i];
	}
	int begin1 = clock();
	InsertSort(a1, N);
	int end1 = clock();

	int begin2 = clock();
	ShellSort(a2, N);
	int end2 = clock();

	int begin3 = clock();
	SelectSort(a3, N);
	int end3 = clock();

	int begin4 = clock();
	HeapSort(a4, N);
	int end4 = clock();

	int begin5 = clock();
	QuickSort(a5, 0, N - 1);
	int end5 = clock();

	int begin6 = clock();
	MergeSort(a6, N);
	int end6 = clock();

	int begin7 = clock();
	BubbleSort(a7, N);
	int end7 = clock();

	printf("InsertSort:%d\n", end1 - begin1);
	printf("ShellSort:%d\n", end2 - begin2);
	printf("SelectSort:%d\n", end3 - begin3);
	printf("HeapSort:%d\n", end4 - begin4);
	printf("QuickSort:%d\n", end5 - begin5);
	printf("MergeSort:%d\n", end6 - begin6);
	printf("BubbleSort:%d\n", end7 - begin7);

	free(a1);
	free(a2);
	free(a3);
	free(a4);
	free(a5);
	free(a6);
	free(a7);
}


int main()
{
	TestOP();
	//test1();
	return 0;
}

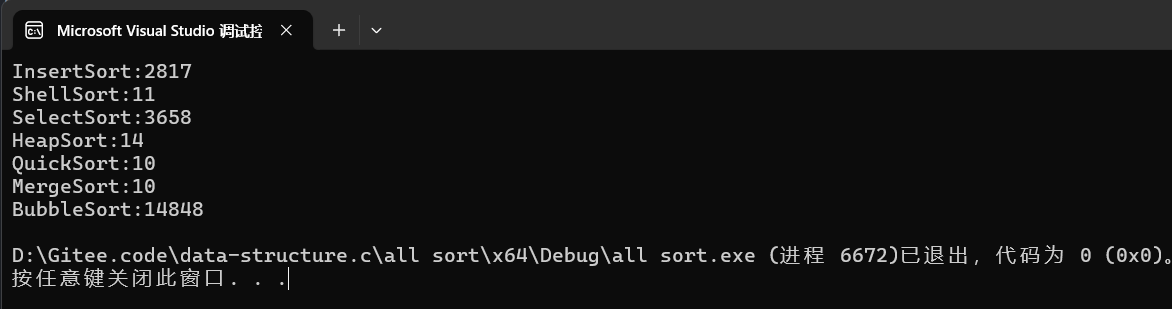
--我们可以通过下图对比一下各个排序的效率

往期回顾：

【数据结构初阶】--排序(一)：直接插入排序，希尔排序

【数据结构初阶】--排序(二)--直接选择排序，堆排序

【数据结构初阶】--排序(三)：冒泡排序，快速排序

结语：到目前为止，我们已经讲将常见的比较类的各种排序都实现完了，在下篇博客中我会为大家介绍一下非比较排序中的计数排序以及总结各种排序的空间复杂度，时间复杂度以及稳定性， 如果文章对你有帮助的话，欢迎评论，点赞，收藏加关注，感谢大家的支持。

相关推荐
凤年徐14 分钟前
【数据结构与算法】刷题篇——环形链表的约瑟夫问题
c语言·数据结构·c++·算法·链表
张子夜 iiii27 分钟前
机器学习算法系列专栏：逻辑回归（初学者）
人工智能·算法·机器学习·逻辑回归
vivo互联网技术27 分钟前
慢SQL优化实战：从一例线上慢SQL探究执行引擎工作过程
数据库·mysql·算法
我想吃烤肉肉31 分钟前
leetcode-python-删除链表的倒数第 N 个结点
python·算法·leetcode·链表
牟同學39 分钟前
深入理解 C++ 中的stdpriority_queue：从原理到实战的高效优先级管理
数据结构·c++·priority_queue
Star在努力44 分钟前
20-C语言：第21~22天笔记
java·c语言·笔记
flashlight_hi1 小时前
LeetCode 分类刷题：16. 最接近的三数之和
javascript·数据结构·算法·leetcode
艾莉丝努力练剑1 小时前
【C/C++】形参、实参相关内容整理
c语言·开发语言·c++·学习
彭军辉1 小时前
什么是抽象主义人工智能？
人工智能·算法·语言模型·机器人
热门推荐
01Qwen3-Coder 快速上手教程 | Qwen Code + Claude Code02全球最强模型Grok4，国内已可免费使用！（附教程）03UV安装并设置国内源04ChatGPT 5发布日期揭秘：2025年8月上线，多模态推理能力全面升级05KGG转MP3工具|非KGM文件|解密音频06腾讯还是太全面了，限时免费！超全CodeBuddy IDE保姆级教程！（附案例）07如何在 Cursor 中继续使用 Claude08Cursor 终端“卡死/无响应”问题的解法09Claude Code 效率实战指南：从入门到精通的实用技巧（附安装教程）10NVIDIA显卡驱动、CUDA、cuDNN 和 TensorRT 版本匹配指南