论文:Dual-path Image Inpainting with Auxiliary GAN Inversion
paper:Dual-path Image Inpainting with Auxiliary GAN Inversion | IEEE Conference Publication | IEEE Xplore
code:无
1:GAN Inversion
GAN反演 ( GAN Inversion ) 的目的是基于预训练的 GAN 模型找到最接近的 latent code,以恢复输入图像。
GAN 反演主要分为两类:基于优化的类型 和 基于学习的类型。
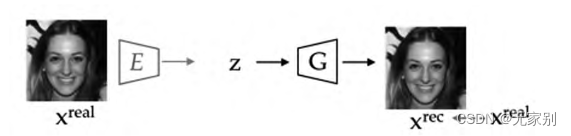
基于学习的 GAN 反演在于训练一个编码器,该编码器可以从给定的图像中推断 latent code(提取图像潜在特征),通过预训练的 GAN 生成器生成反演图像,从而通过最小化反演图像和原始图像之间损失来直接优化 latent code(通过训练编码器的形式)。大致结构如下:
图1:
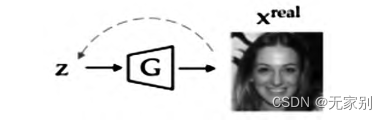
基于优化的 GAN 反演在于通过输入一个随机张量到一个预训练的 GAN 生成器,使生成器产生反演图像,从而通过最小化反演图像和原始图像之间损失来直接优化 latent code(通过训练生成器的形式)。大致结构如下:
图 2:
现在的主流方法除了以上两类以外还有两者的混合方法:使用编码器获取一个大致的 latent code 再优化生成器使其拟合原始图像的 latent code 达到结合两者优势的目的。
2:模型架构
作者提出了一种通过使用 GAN 反演来辅助一个前馈神经网络来进行图像修复的模型。
该框架由两条路径组成:前馈路径和反转路径。
在反演路径中,预训练的 GAN 生成器在 latent space 中寻找在损坏图像中,其反演图像与观测区域距离最近的 latent code。在这里作者采用的是基于学习的反演策略。然后作者并没有直接采用 GAN 反演的结果作为图像修复的最终结果,而是将生成器中学习到的图像多尺度特征作为一种补充,来补充到前馈路径中。
在前馈路径中,作者使用自编码器网络 ( auto-encoder network )对损坏的图像进行修复,在此过程中,将来自反演路径的多尺度特征集成到解码器中。
主要模型架构如下:
图3:
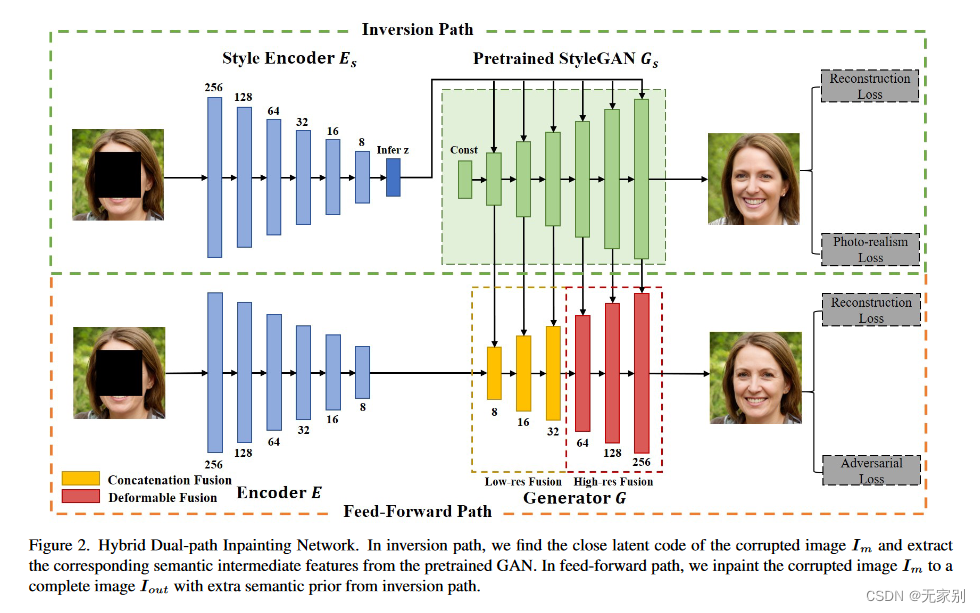
这个地方有个值得注意的点在于:反演路径到前馈路径的两个生成器之间的特征并不是简单的进行拼接的。原因作者说:由于反演路径的推断不准确或输入结果的不确定性,反演路径的结果可能与前馈路径的结果在空间上不对齐。这个问题也存在于语义中间特征中,这些特征在前馈路径中被馈送到生成器G中,并且会降低最终的喷漆结果。这种不对齐问题不能通过简单地连接反转路径和前馈路径的特征来很好地解决。
原文:Due to the inaccurate inference in the inversion path or the uncertainty of inpainted results, the results from the inversion path may be spatially misaligned with the feedforward path results. This issue also exists in semantic intermediate features which are fed into generator G in the feed-forward path and would degrade the final inpainting results. This misalignment issue can not be well addressed by simply concatenating features from the inversion path and the feed-forward path.
这种不确定性主要来源于生成器生成的图像像素逐层提高的原因。这使得某些在低像素时处在同一个位置的特征,在超分辨率后发生了偏移,就导致了两者的不对齐。
所以作者在两者中间加入了一个用于对齐的神经网络。
该对齐神经网络类似于 DCNv2 (可变形卷积网络)。在这个模块中,对反演路径中目标点的偏移量进行预测,这样可以获得与前馈路径中目标点更多相似的信息。这样,反演路径中的局部特征可以更好地与前馈路径中的局部特征对齐。具体如下图:
图4:

左边是简单的融合,右边是作者的方法。简单来说就是先简单融合后,对融合出来的特征预测一个 f s i f^{i}{s} fsi 中每个点的位置偏移和调制权值。位置偏移 m o i m^{i}{o} moi(图中的 Offset Map)表示 f s i f^{i}{s} fsi 与 f g i f^{i}{g} fgi 中对齐的采样点位置的偏差,调制权值 m w i m^{i}{w} mwi(图中的 Modulated Weight Map)表示不同采样点的重要性。将 m o i m^{i}{o} moi 、 m w i m^{i}{w} mwi 和 f s i f^{i}{s} fsi 输入到 DCNv2 中得到对齐的特征 f s ^ i \hat{f_{s}}^{i} fs^i 。最后再将 f s ^ i \hat{f_{s}}^{i} fs^i 和 f g i f^{i}_{g} fgi 做简单融合作为输入生成器下一层的特征。这一步骤可表示为:
m o i , m w i = P i ( Concat ( f s i , f g i ) ) , f ^ s i = DFConv ( m o i , m w i , f s i ) , f g i + 1 = L i ( Concat ( f ^ s ′ f g i ) ) , \begin{aligned} \boldsymbol{m}{o}^{i}, \boldsymbol{m}{w}^{i} & =P^{i}\left(\operatorname{Concat}\left(\boldsymbol{f}{s}^{i}, \boldsymbol{f}{g}^{i}\right)\right), \\ \hat{\boldsymbol{f}}{s}^{i} & =\operatorname{DFConv}\left(\boldsymbol{m}{o}^{i}, \boldsymbol{m}{w}^{i}, \boldsymbol{f}{s}^{i}\right), \\ \boldsymbol{f}{g}^{i+1} & =L^{i}\left(\operatorname{Concat}\left(\hat{\boldsymbol{f}}{s}^{\prime} \boldsymbol{f}_{g}^{i}\right)\right), \end{aligned} moi,mwif^sifgi+1=Pi(Concat(fsi,fgi)),=DFConv(moi,mwi,fsi),=Li(Concat(f^s′fgi)),
这里的 i i i 只取 3,4,5 即:只取分辨率为 64*64, 128*128, 256*256 三种分辨率的图像特征做上述过程。(主要原因可能还是在于不让模型过于复杂)
3:损失函数
损失函数就是 GAN 中常用的老几样:
反演路径 :
1:用于判别器 D D D 的感知损失:(其中 D s D_{s} Ds 为预训练的判别器)
L s p = log ( 1 − D s ( G s ( z ) ) ) \mathcal{L}{s p}=\log \left(1-D{s}\left(G_{s}(\boldsymbol{z})\right)\right) Lsp=log(1−Ds(Gs(z)))
2:训练编码器 E s E_{s} Es 的重构损失:
L s r = ∣ ∣ I g t − I s ∣ ∣ 1 L_{sr} = ||I_{gt}-I_{s}||_{1} Lsr=∣∣Igt−Is∣∣1
整个反演路径的损失:
L i n v = L s p + λ s r L s r L_{inv}=L_{sp}+\lambda_{sr}L_{sr} Linv=Lsp+λsrLsr
前馈路径 :
1:最终输出的图像和原始图像之间的损失:
L r = ∣ ∣ I g t − I g ∣ ∣ 1 L_{r} = ||I_{gt}-I_{g}||_{1} Lr=∣∣Igt−Ig∣∣1
2:为了使最终结果 I g I_{g} Ig 更加真实的对抗损失:
L a d v D = − E I g t [ log D ( I g t ) ] − E I g log [ 1 − D ( I g ) ] L_{adv}^{D}=-\mathbb{E} {I{gt}}\left [ \log D\left ( I_{gt} \right ) \right ] -\mathbb{E}{I{g}}\log\left [ 1-D(I_{g}) \right ] LadvD=−EIgt[logD(Igt)]−EIglog[1−D(Ig)]
整个前馈路径的损失:
L f f = λ r L r + L a d v L_{ff}=\lambda_{r}L_{r}+L_{adv} Lff=λrLr+Ladv
上述中的 λ s r \lambda_{sr} λsr 和 λ r \lambda_{r} λr 都为超参数,默认设定为 20.