【R语言】地理探测器模拟及分析（Geographical detector）

地理探测器模拟及分析

[1. 写在前面](#1. 写在前面)
[2. R语言实现](#2. R语言实现)
- [2.1 数据导入](#2.1 数据导入)
- [2.2 确定数据离散化的最优方法与最优分类](#2.2 确定数据离散化的最优方法与最优分类)
- [2.3 分异及因子探测器（factor detector）](#2.3 分异及因子探测器（factor detector）)
- [2.4 生态探测器（ecological detector）](#2.4 生态探测器（ecological detector）)
- [2.5 交互因子探测器（interaction detector）](#2.5 交互因子探测器（interaction detector）)
- [2.6 风险探测器（risk detector）](#2.6 风险探测器（risk detector）)

1. 写在前面

🗺️🔍地理探测器是一种用于探测空间分异性以及揭示其背后驱动因子的统计学方法。它由中国科学院地理科学与资源研究所的王劲峰研究员 提出，并已被广泛应用于社会环境因素和自然环境因素的影响机理研究。地理探测器模型的核心思想是，如果某个自变量对某个因变量有重要影响，那么自变量和因变量的空间分布应该具有相似性。通过计算和比较各单因子的q值，可以判断它们对空间分异性的解释力，q值越大表示解释力越强。

在当前的研究进展方面，地理探测器已经被应用于多个领域，包括城市扩张驱动力因素分析、健康与风险因子关系的评估、土壤重金属的空间分异及其影响因素分析、青藏高原多年冻土分布影响因子分析等。此外，地理探测器模型的最优离散化研究也取得了进展，这对于提高模型评估结果的精度具有重要意义。

✨✨地理探测器模型的优势在于它没有过多的假设条件，可以克服传统统计方法处理变量所受的限制，因此在空间分析领域得到了广泛的应用和认可。随着研究的深入，地理探测器模型也在不断地优化和发展，以适应更多领域的研究需求。

当前已有很多的中英文文献涉及到了地理探测器，地理探测器主要包括了因子探测器、交互探测器、风险探测器和生态探测，其中因子探测器和交互探测器使用较为广泛。我个人人为交互探测器可以探测不同环境因子的交互作用，可以更加深刻地认识到环境变量之间的非线性、非对称和动态影响。

2. R语言实现

为了方便，我任意选择了一个数据集，数据内容如下：

其中Y为响应变量（因变量），X为自变量，一共2000个样本。此外，X5、X9和X10为类别型变量（离散变量）。

2.1 数据导入

首先进行相关包和数据导入，这里我们使用了地探测器"GD"包 。此外，需要注意的是，read_exce() 函数导入的数据为tibble格式，但是GD中需要数据框格式，否则会报错，因此需要对数据格式进行转换：

r 复制代码

library(GD)
library(openxlsx)
library(readxl)
setwd("D:/2007lucc")
data<-read_excel("result.xlsx")
View(data)
str(data)
# 将tibble数据格式转换为data.frame格式
data <- as.data.frame(data) 
#class(data) # 查看数据类型，此时应为data.frame
str(data)

数据结构：

r 复制代码

> str(data)
'data.frame':	2000 obs. of  11 variables:
 $ Y  : num  97 97 97 97 97 97 97 97 89 105 ...
 $ X1 : num  17.1 17.6 16.8 16.8 17 ...
 $ X2 : num  -2.45 -2.07 -2.48 -2.43 -2.37 ...
 $ X3 : num  68 68 69.4 68.4 68.4 ...
 $ X4 : num  993 1006 858 961 967 ...
 $ X5 : num  4 4 4 4 4 4 4 4 4 4 ...
 $ X6 : num  446 306 491 393 331 552 422 482 286 638 ...
 $ X7 : num  191 148 151 207 286 ...
 $ X8 : num  5.96 5.19 1.47 2.98 1.04 ...
 $ X9 : num  4 4 4 4 4 4 4 4 4 4 ...
 $ X10: num  23111112 23115192 23111112 23110140 23111112 ...

2.2 确定数据离散化的最优方法与最优分类

在进行地理探测器分析之前，需要对连续变量进行离散化操作，并且找到最佳离散类别，已进行更好的分析模拟。离散化方法主要包括：equal，natural，quantile，geometric和sd，通过optidisc（）函数可以自动选择最优离散化方法和类别数。

r 复制代码

#多个变量，包括连续变量
discmethod <-c("equal","natural","quantile","geometric","sd")
discitv <-c(3:7) #离散分类的数量，3到7类，建议不要分太多的类别，否则optidisc()函数运行时间过长
dataFin <- data
data.continuous <- dataFin[, c(1:5, 7:9)] # 只对连续变量进行离散化，一共有7个连续变量
#数据离散化
odc1 <-optidisc(Y~., data = data.continuous ,discmethod, discitv) # 这一步比较耗时，大概几分钟到几十分钟
dim(data.continuous)
plot(odc1)
data.continuous  <-do.call(cbind,lapply(1:7,function(x)data.frame(
                                 cut(data.continuous [, -1][, x],
                                     unique(odc1[[x]]$itv),
                                     include.lowest =TRUE))))
dataFin[,c(2:5, 7:9)] <-data.continuous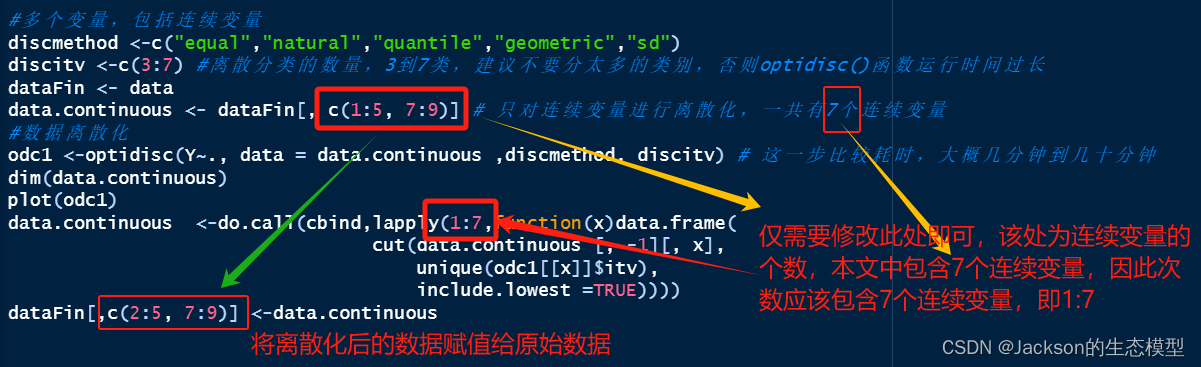

结果展示：

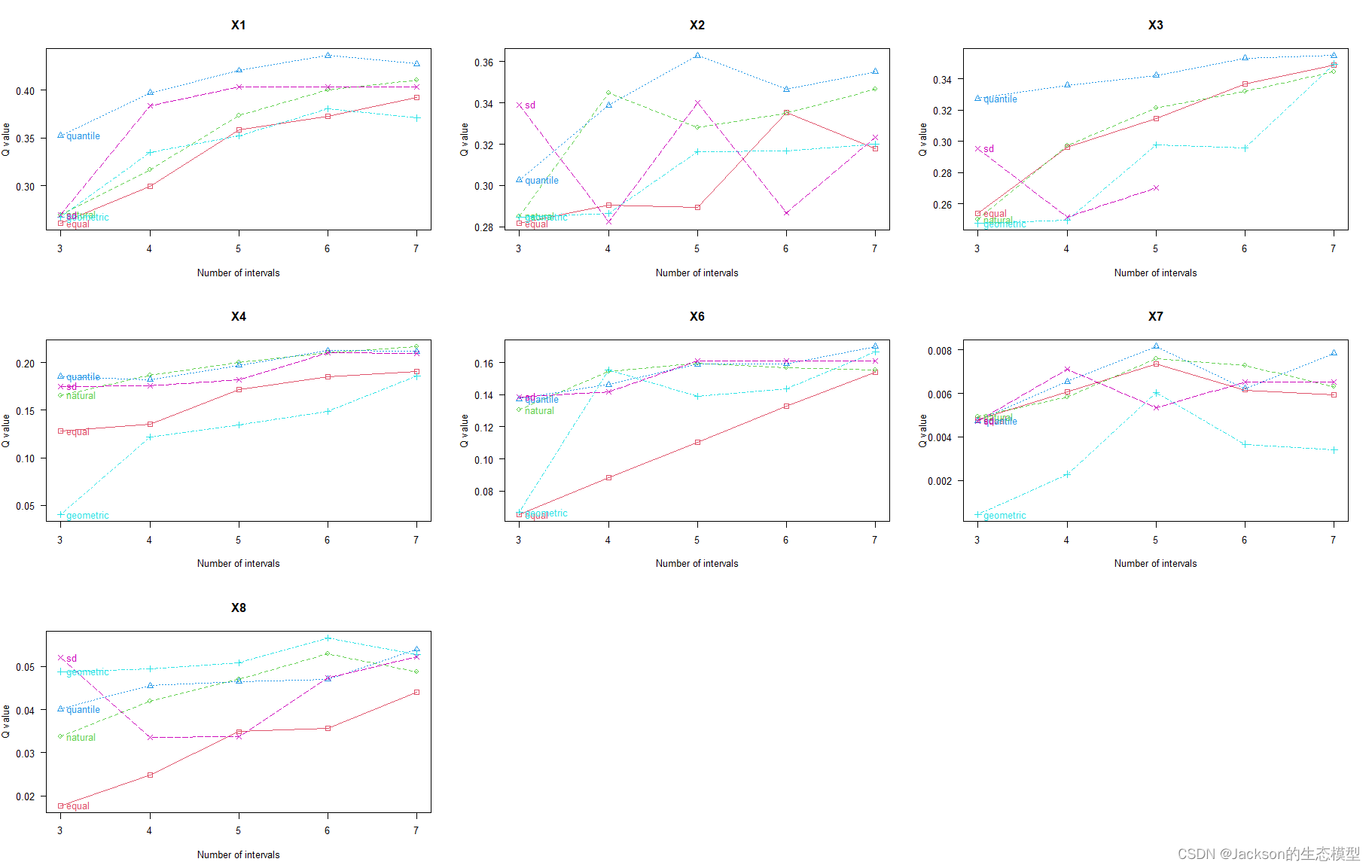
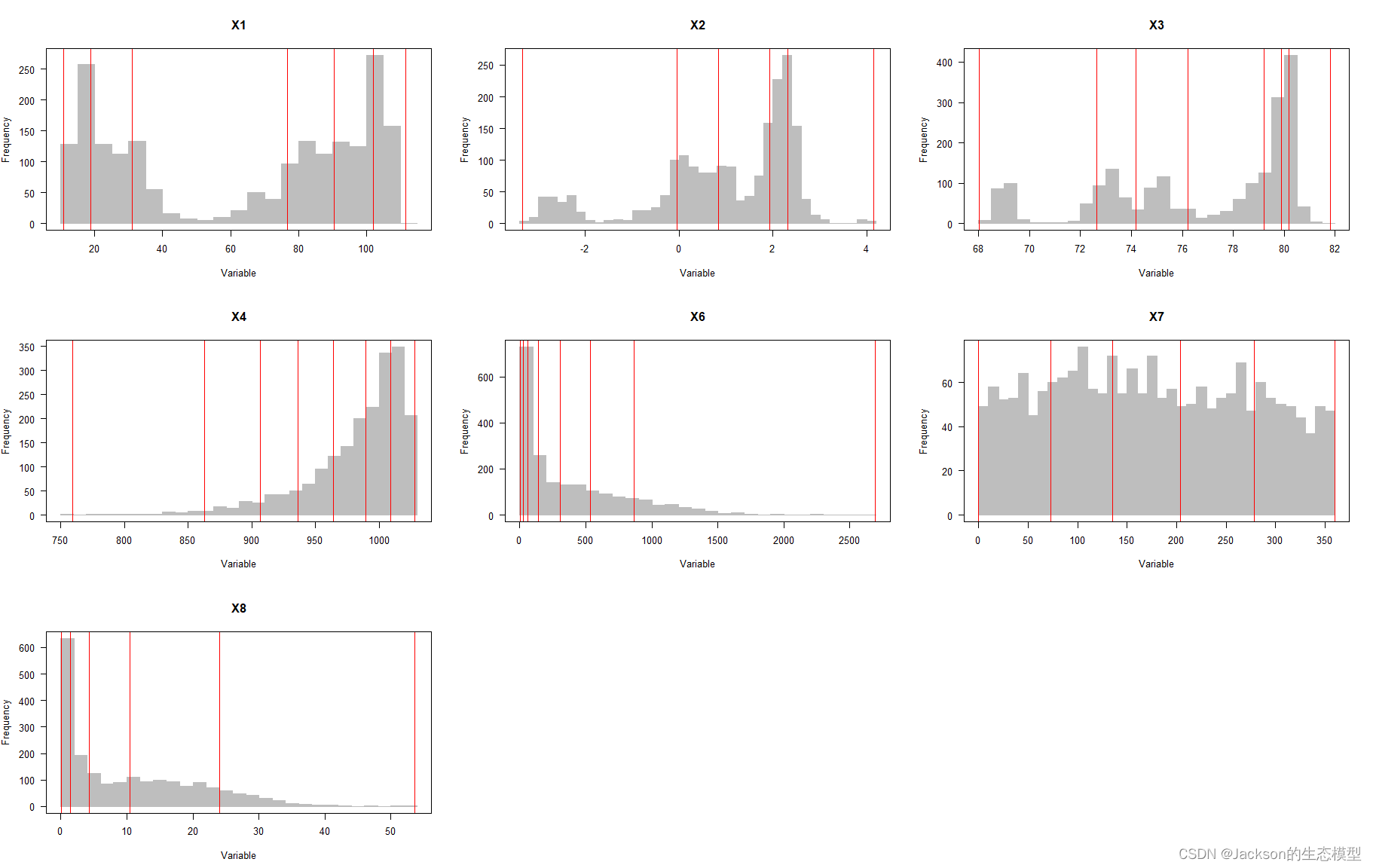
数据准备好之后就可以进行地理探测器（GD）分析了！！！

2.3 分异及因子探测器（factor detector）

分异及因子探测主要用于探测Y的空间分异性；以及探测某因子X多大程度上解释了属性Y的空间分异，用q值度量。简单点来说就是环境变量对因变量的贡献度。

写论文的时候，尽量将以上原理和公示进行展示和补充。

r 复制代码

# 单因子探测器
gd <-gd(Y~., data = dataFin[,c(1, 2:11)])
gd
plot(gd)

r 复制代码

> gd
   variable         qv          sig
1        X1 0.43614146 1.387049e-10
2        X2 0.36292021 2.817672e-10
3        X3 0.35501601 8.356258e-10
4        X4 0.21368849 7.493217e-10
5        X5 0.11939089 6.191341e-10
6        X6 0.16985611 2.561658e-10
7        X7 0.00815299 2.947367e-03
8        X8 0.05664708 3.956563e-10
9        X9 0.23192232 3.588341e-10
10      X10 0.35382549 4.703113e-03

2.4 生态探测器（ecological detector）

生态探测主要用于比较两因子X1和X2对属性Y的空间分布的影响是否有显著的差异

r 复制代码

# 生态探测器
gdeco <-gdeco(Y~., data = dataFin[,c(1, 2:11)])
gdeco
plot(gdeco)

r 复制代码

> gdeco
Ecological detector:
   variable   X1   X2   X3   X4   X5   X6   X7   X8   X9  X10
1        X1 <NA> <NA> <NA> <NA> <NA> <NA> <NA> <NA> <NA> <NA>
2        X2    Y <NA> <NA> <NA> <NA> <NA> <NA> <NA> <NA> <NA>
3        X3    Y    N <NA> <NA> <NA> <NA> <NA> <NA> <NA> <NA>
4        X4    Y    Y    Y <NA> <NA> <NA> <NA> <NA> <NA> <NA>
5        X5    Y    Y    Y    Y <NA> <NA> <NA> <NA> <NA> <NA>
6        X6    Y    Y    Y    Y    Y <NA> <NA> <NA> <NA> <NA>
7        X7    Y    Y    Y    Y    Y    Y <NA> <NA> <NA> <NA>
8        X8    Y    Y    Y    Y    Y    Y    Y <NA> <NA> <NA>
9        X9    Y    Y    Y    Y    Y    Y    Y    Y <NA> <NA>
10      X10    Y    N    N    Y    Y    Y    Y    Y    Y <NA>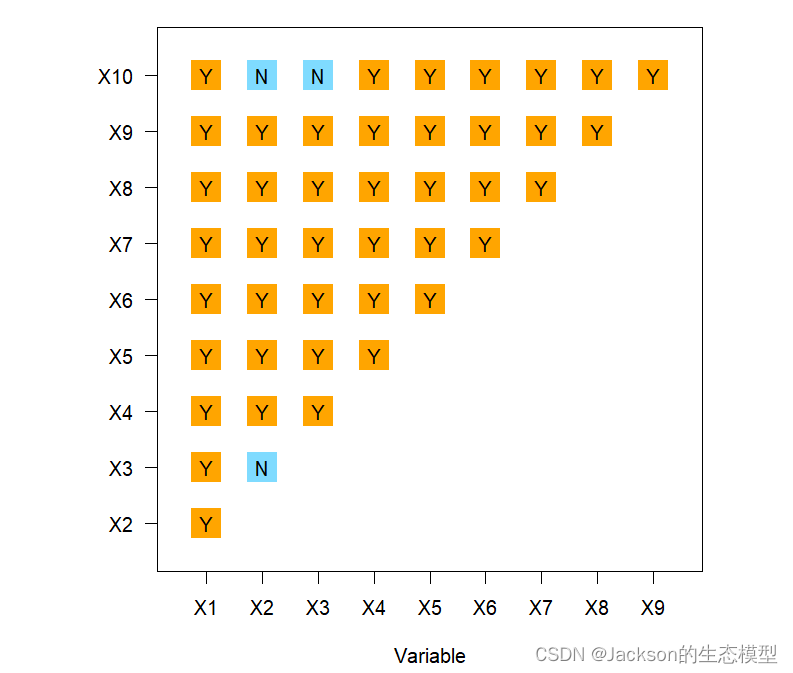

2.5 交互因子探测器（interaction detector）

交互探测器共包含了5种类别，但根据以往的经验，结果以增强或非线性增强作用为主。

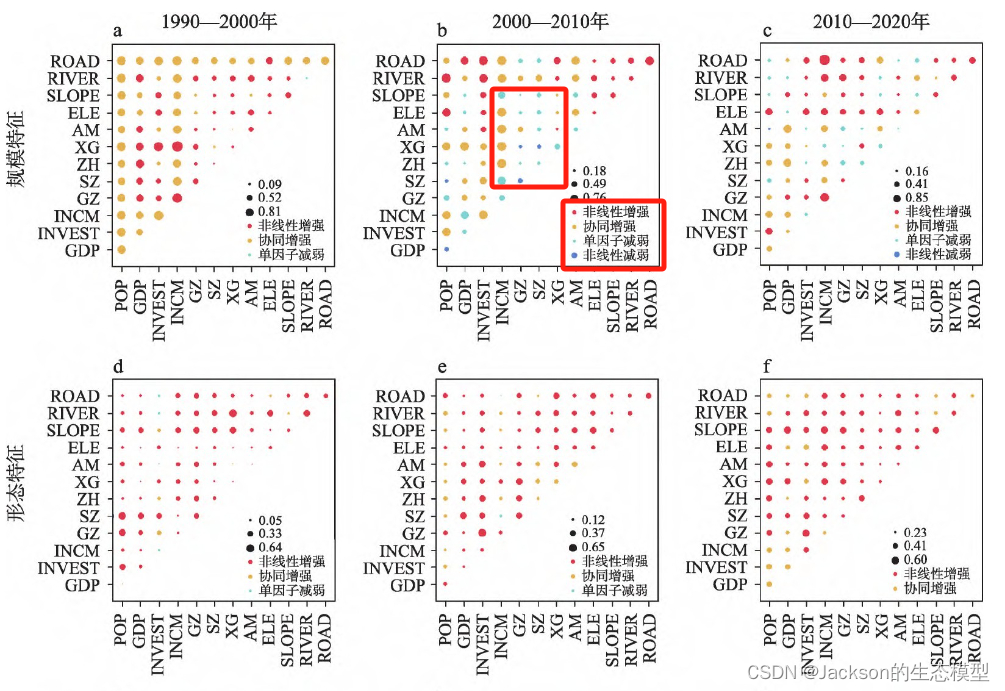
这里我选择了一篇论文的交互作用的结果，其中包含了4种类别的交互作用结果。

r 复制代码

# 交互作用探测器
gdint <-gdinteract(Y~., data = dataFin[,c(1, 2:11)])
gdint
plot(gdint)

r 复制代码

> gdint
Interaction detector:
   variable     X1     X2     X3     X4     X5     X6     X7     X8     X9 X10
1        X1     NA     NA     NA     NA     NA     NA     NA     NA     NA  NA
2        X2 0.4821     NA     NA     NA     NA     NA     NA     NA     NA  NA
3        X3 0.4750 0.4374     NA     NA     NA     NA     NA     NA     NA  NA
4        X4 0.4675 0.4335 0.4599     NA     NA     NA     NA     NA     NA  NA
5        X5 0.4491 0.3925 0.3918 0.3180     NA     NA     NA     NA     NA  NA
6        X6 0.4755 0.4038 0.4377 0.3242 0.3044     NA     NA     NA     NA  NA
7        X7 0.4476 0.3737 0.3636 0.2254 0.1277 0.1890     NA     NA     NA  NA
8        X8 0.4573 0.3837 0.4029 0.2505 0.1910 0.1989 0.0693     NA     NA  NA
9        X9 0.4697 0.4158 0.3823 0.3602 0.2698 0.3462 0.2394 0.2902     NA  NA
10      X10 0.5265 0.4758 0.4726 0.4445 0.3775 0.4457 0.3770 0.4073 0.4016  NA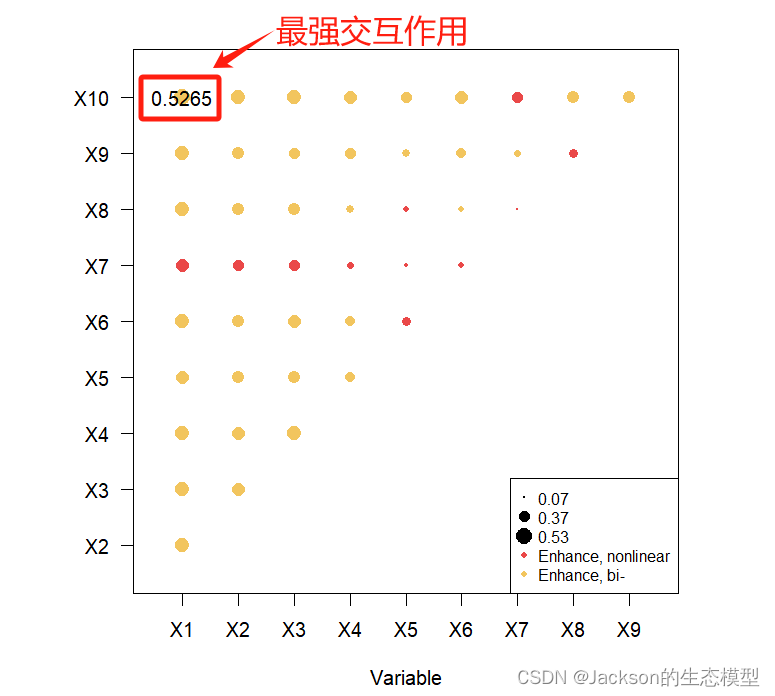

总体而言，因子交互作用的结果表现为增强或者非线性增强。

2.6 风险探测器（risk detector）

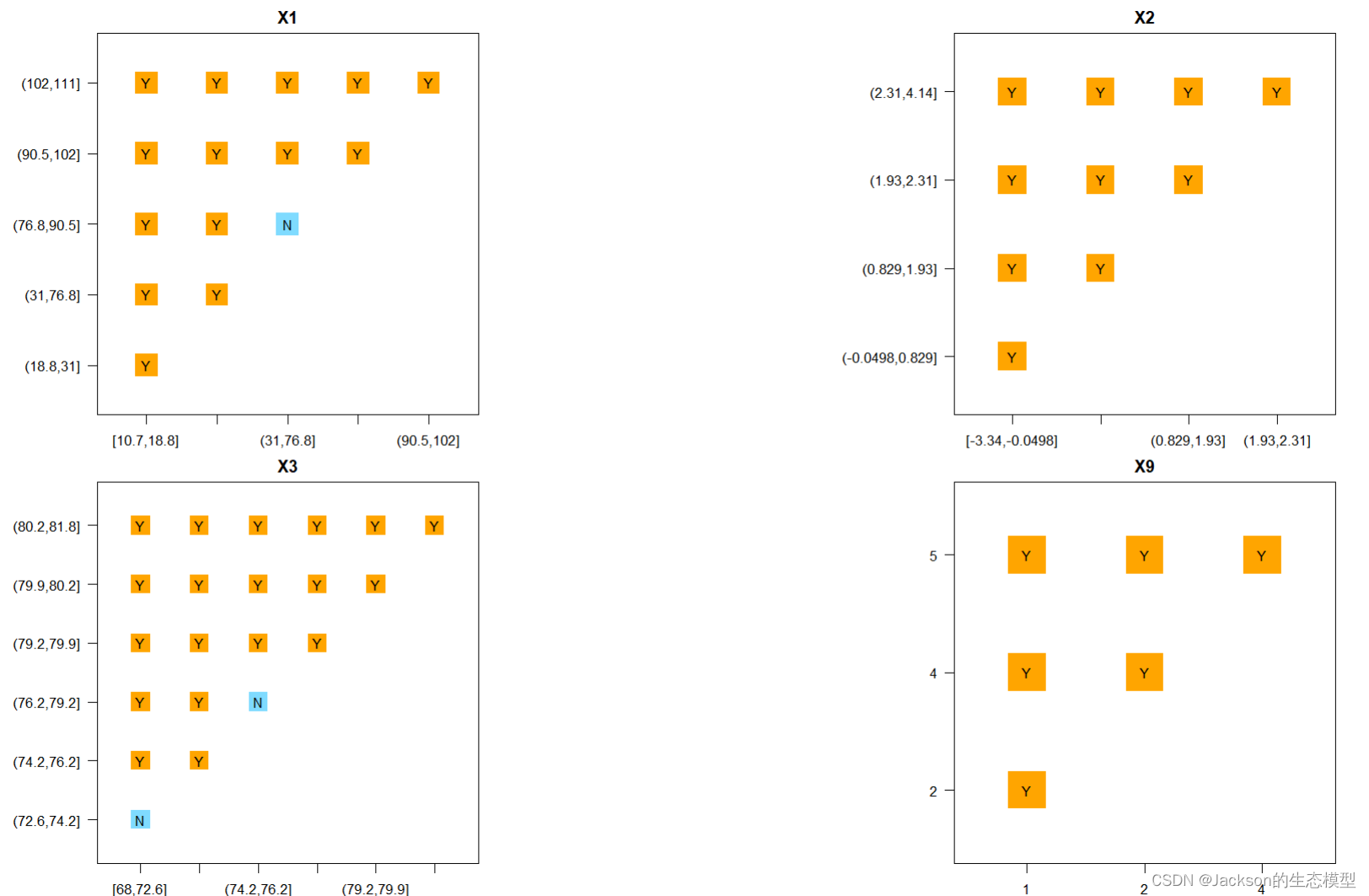
判断两个子区域间的属性均值是否有显著的差别。若为N，则表示不显著，即两个子区域内属性均值无差别。若为Y，则有显著差别。

r 复制代码

## 风险因子探测器
# 显著性
gdrisk <-gdrisk(Y~X1+X2+X3+X9, data = dataFin[,c(1, 2:11)])
gdrisk
plot(gdrisk)
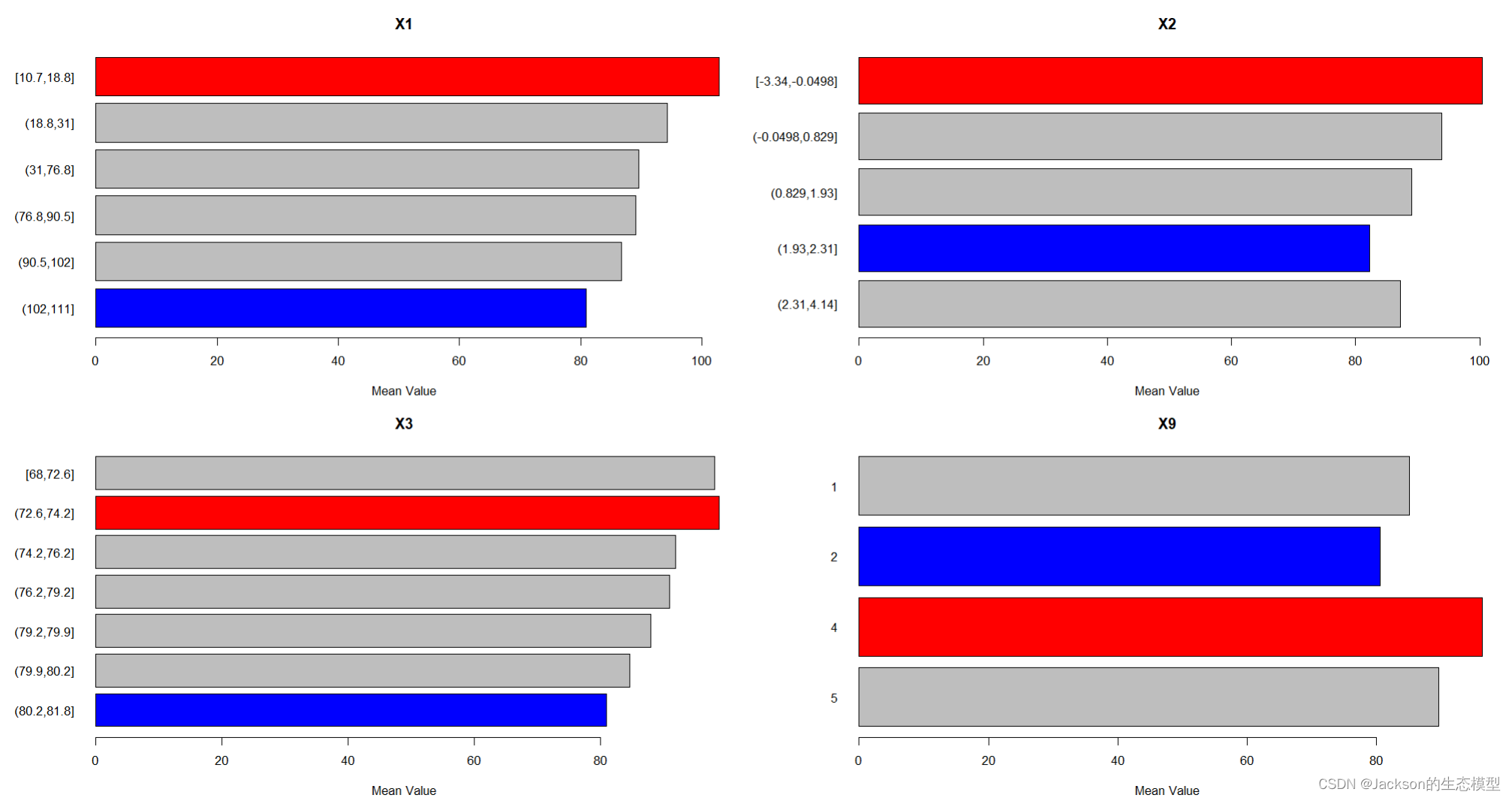
# 风险探测(平均风险)
riskmean <- riskmean(Y~X1+X2+X3+X9, data = dataFin[,c(1, 2:11)])
riskmean
plot(riskmean)