A. 数列修改求和
题目描述:
有一个 n 个数的整数数列。现可以对数列做 2 种不同的操作:
-
修改:在数组的第 x 个数上增加值 y ;
-
求和:求数组的第 x 到第 y 个数的和,包含 x 和 y 两个位置;
输入:
第 1 行输入 2 个整数 n、m,分别代表数列中元素个数 以及 操作次数。(n,m≤10^5)。
第 2 行输入 n 个整数,用空格隔开。
接下来 m 行,每行有 3 个整数 k、x、y,如果 k=0 ,表示求数列中区间 [x,y] 之间所有数的和,k=1 表示在第 x 数上加上值 y 。
(测试数据保证 k、x、y 三个整数的合理性(1≤x≤n),也确保所有数据在运算后依然在 int 的范围内)
输出:
输出若干行,按照读入的顺序输出 k=0 时求出的区间和。
样例:
输入:
10 5 1 2 3 4 5 6 7 8 9 10 1 1 5 0 1 3 0 4 8 1 7 5 0 4 8
输出:
11 30 35
代码如下:
cpp
#include<bits/stdc++.h>
using namespace std;
const int N=1e5;
int c[N];
int n,m;
int lowbit(int x){
return x&-x;
}
void add(int x,int y){
for(int i=x;i<=n;i=i+lowbit(i)){
c[i]+=y;
}
}
int query(int x){
int res=0;
for(int i=x;i>0;i=i-lowbit(i)){
res+=c[i];
}
return res;
}
int main(){
scanf("%d%d",&n,&m);
int k,x,y;
for(int i=1;i<=n;i++){
scanf("%d",&x);
add(i,x);
}
while(m--){
scanf("%d%d%d",&k,&x,&y);
if(k==0) printf("%d\n",query(y)-query(x-1));
else add(x,y);
}
return 0;
}B. 星星的等级
题目描述:
天空中有一些星星,这些星星都在不同的位置,每个星星有个坐标。如果一个星星的左下方(包含正左和正下)有 k 颗星星,就说这颗星星是 k 级的。
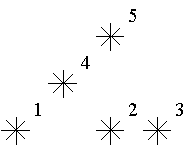
例如,上图中星星 5 是 3 级的(1,2,4 在它左下),星星 2,4 是 1 级的。例图中有 1 个 0 级,2 个 1 级,1 个 2 级,1 个 3 级的星星。
给定星星的位置,输出各级星星的数目。
输入:
第一行一个整数 N,表示星星的数目;
接下来 N 行给出每颗星星的坐标,坐标用两个整数 x,y 表示;
不会有星星重叠。星星按 y 坐标增序给出,y 坐标相同的按 x 坐标增序给出。
对于全部数据,1≤N≤1.5×10^4,0 ≤ x,y ≤ 3.2×10^4 。
输出:
N 行,每行一个整数,分别是 0 级,1 级,2 级,... ,N−1 级的星星的数目。
样例:
输入:
5 1 1 5 1 7 1 3 3 5 5
输出:
1 2 1 1 0
代码如下:
cpp
#include<bits/stdc++.h>
using namespace std;
const int N=1.5e4+10,M=3.2e4+10;
int c[M],r[N];
int n;
int lowbit(int x){
return x&-x;
}
void add(int x,int y){
for(int i=x;i<=32001;i=i+lowbit(i)){
c[i]+=y;
}
}
int sum(int x){
int res=0;
for(int i=x;i>0;i=i-lowbit(i)){
res+=c[i];
}
return res;
}
int main(){
scanf("%d",&n);
int x,y;
for(int i=1;i<=n;i++){
scanf("%d%d",&x,&y);
x++;
r[sum(x)]++;
add(x,1);
}
for(int i=0;i<=n-1;i++){
printf("%d\n",r[i]);
}
return 0;
}C. 校门外的树
题目描述:
校门外有很多树,学校决定在某个时刻在某一段种上一种树,保证任一时刻不会出现两段相同种类的树,现有两种操作:
-
K=1,读入 l,r 表示在 l 到 r 之间种上一种树,每次操作种的树的种类都不同;
-
K=2,读入 l,r 表示询问 l 到 r 之间有多少种树。
注意:每个位置都可以重复种树。
输入:
第一行 n,m 表示道路总长为 n,共有 m 个操作;
接下来 m 行为 m 个操作。
输出:
对于每个 k=2 输出一个答案。
样例:
输入:
5 4 1 1 3 2 2 5 1 2 4 2 3 5
输出:
1 2
代码如下:
cpp
#include<bits/stdc++.h>
using namespace std;
const int N=5e4+10;
int cl[N],cr[N];
int n,m;
int lowbit(int x){
return x&-x;
}
void add(int x,int y,int c[]){
for(int i=x;i<=n;i=i+lowbit(i)){
c[i]+=y;
}
}
int query(int x,int c[]){
int res=0;
for(int i=x;i>0;i=i-lowbit(i)){
res+=c[i];
}
return res;
}
int main(){
scanf("%d%d",&n,&m);
int k,l,r;
while(m--){
scanf("%d%d%d",&k,&l,&r);
if(k==1) add(l,1,cl),add(r,1,cr);
else printf("%d\n",query(r,cl)-query(l-1,cr));
}
return 0;
}