自动微分
自动微分是利用链式法则来自动计算一个复合函数的梯度。基本原理是将所有数值计算分解为一些基本操作和初等函数(算子),然后利用链式法则自动计算复合函数的梯度。
例如对下式求解微分,
f ( x ; w , b ) = 1 exp ( − ( w x + b ) ) + 1 f(x;w,b)=\frac{1}{\exp(-(wx+b))+1} f(x;w,b)=exp(−(wx+b))+11
首先提取出上式中的算子,从最内层自变量 x x x开始按计算顺序向外依次可以提取出: × , + , × , exp , + , ÷ \times,+,\times,\exp,+,\div ×,+,×,exp,+,÷,依照这个顺序可以建立计算图
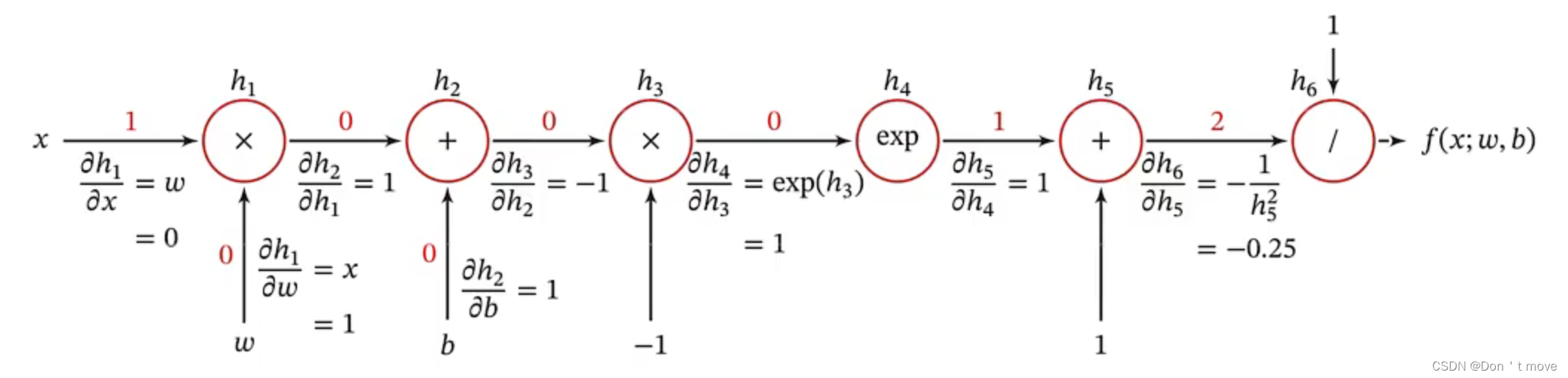
上图中每个节点都是一个算子操作,两个指向算子的箭头表示参与运算的变量,每个箭头上又计算了经过结合后的式子 h h h对每个参与运算的变量的偏导数(红色数字代表变量取值,上图示例为 x = 1 , w = 0 , b = 0 x=1,w=0,b=0 x=1,w=0,b=0)。最后,根据链式法则,某个式子 f f f对于某个变量 x x x的偏导数,就是从变量 x x x到式子 f f f的路径上的所有偏导数(或带入取值后的偏导数值)的连乘。
如果函数和参数之间有多条路径,可以将这多条路径上的导数再进行相加,得到最终的梯度。(原理还是链式法则)

因此 f ( x ; w , b ) f(x;w,b) f(x;w,b)对 w w w的偏导数就是
∂ f ( x ; w , b ) ∂ w = ∂ h 1 ∂ w ∂ h 2 ∂ h 1 ∂ h 3 ∂ h 2 ∂ h 4 ∂ h 3 ∂ h 5 ∂ h 4 ∂ h 6 ∂ h 5 = x × 1 × − 1 × exp ( h 3 ) × 1 × − 1 h 5 2 = x h 5 2 exp ( h 3 ) = x exp ( − ( w x + b ) ) ( exp ( − ( w x + b ) ) + 1 ) 2 \begin{aligned} \frac{\partial f(x;w,b)}{\partial w} &=\frac{\partial h_1}{\partial w}\frac{\partial h_2}{\partial h_1}\frac{\partial h_3}{\partial h_2}\frac{\partial h_4}{\partial h_3}\frac{\partial h_5}{\partial h_4}\frac{\partial h_6}{\partial h_5}\\ &=x\times1\times-1\times\exp(h_3)\times1\times-\frac{1}{h_5^2}\\ &=\frac{x}{h_5^2}\exp(h_3)\\ &=\frac{x\exp(-(wx+b))}{(\exp(-(wx+b))+1)^2} \end{aligned} ∂w∂f(x;w,b)=∂w∂h1∂h1∂h2∂h2∂h3∂h3∂h4∂h4∂h5∂h5∂h6=x×1×−1×exp(h3)×1×−h521=h52xexp(h3)=(exp(−(wx+b))+1)2xexp(−(wx+b))
或者直接带值 = 1 × 1 × − 1 × 1 × 1 × − 0.25 = 0.25 =1\times1\times-1\times1\times1\times-0.25=0.25 =1×1×−1×1×1×−0.25=0.25
在利用计算图进行自动微分计算时,有两种计算顺序,分别为前向模式和反向模式。
- 前向模式 是指计算时按照计算图中从前向后的顺序,每计算出一个偏导数就令其与上一层计算出的偏导数相乘从而得到函数对这一层变量的梯度( f ( x ) = ∂ h 1 ∂ w ∂ h 2 ∂ h 1 ∂ f ( x ) ∂ h 2 f(x)=\frac{\partial h_1}{\partial w}\frac{\partial h_2}{\partial h_1}\frac{\partial f(x)}{\partial h_2} f(x)=∂w∂h1∂h1∂h2∂h2∂f(x))。上面示例过程就是属于前向模式。
- 反向模式 是指计算时按照计算途中从后向前的顺序,先按照计算图从前向后顺序将所有偏导数计算出来,然后再从最后一个开始,从后向前求梯度( f ( x ) = ∂ f ( x ) ∂ h 1 ∂ h 1 x f(x)=\frac{\partial f(x)}{\partial h_1}\frac{\partial h_1}{x} f(x)=∂h1∂f(x)x∂h1)。该过程与反向传播算法思想相同。
二者的区别在于实际编程过程中,前向模式的计算机内存消耗要大于反向模式的内存消耗,例如对于存在三个算子的计算图:前向计算过程为 f ( x ) = ∂ h 1 ∂ w ∂ h 2 ∂ h 1 ∂ f ( x ) ∂ h 2 f(x)=\frac{\partial h_1}{\partial w}\frac{\partial h_2}{\partial h_1}\frac{\partial f(x)}{\partial h_2} f(x)=∂w∂h1∂h1∂h2∂h2∂f(x),其中需要存储的变量有三个;反向模式计算过程为 f ( x ) = ∂ f ( x ) ∂ h 1 ∂ h 1 w f(x)=\frac{\partial f(x)}{\partial h_1}\frac{\partial h_1}{w} f(x)=∂h1∂f(x)w∂h1,其中只需要存储两个变量,且对于有任意个算子的计算图,反向模式都只需要存储2个变量。

反向传播算法事实上就是自动微分的反向模式,对前馈神经网络的训练过程可以分为以下三步:
- 前向计算每一层的状态和激活值,直到最后一层
- 反向计算每一层的参数和偏导数
- 更新参数
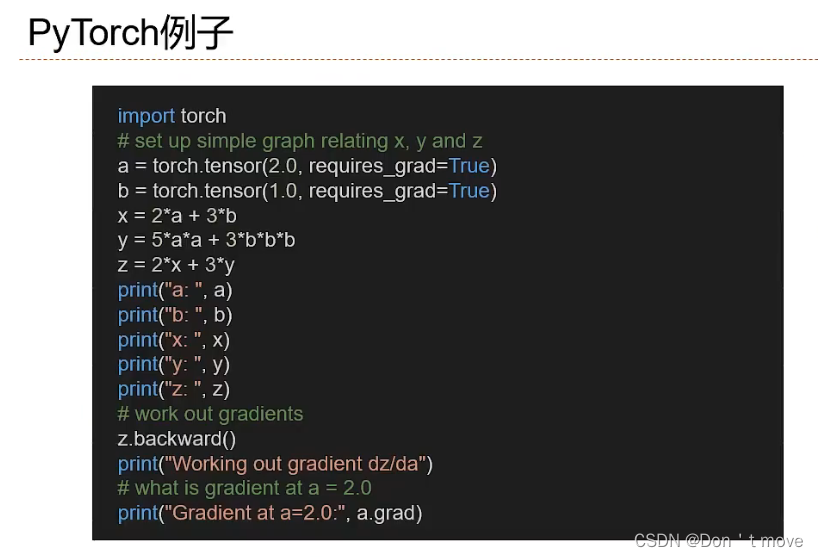
此外,计算图还分为两种:
- 静态计算图:是再编译时构建计算图,构建好后在程序运行过程中不能改变(Theano和Tensorflow)。静态计算图在构建时可以进行优化,并行能力强,但灵活性较差。
- 动态计算图:在程序运行时,根据神经网络结构变化(输入特征为变长序列)而动态构建(DyNet、Chainer和PyTorch)。动态计算图不容易优化,当不同输入的网络结构不一致时,难以并行计算,但是灵活性较高。