首先我们来理解一下什么是连续的随机变量 ,在此之前,我们要先理解什么是随机变量 。所谓随机变量 就是在一次随机实验中一组可能的值。比如说抛硬币,我们设正面=100 ,反面=200 ,设随机变量为X ,那么X={100,200} 。 X是我们的随机变量,100,200是一次随机实验中可能的值,硬币是正面还是反面就是随机事件。
随机变量 可以分为离散 和连续两种:
- 离散数据只能够取确定的值,如1,2,3
- 连续数据在一个区间内可以取任意的值(换句话说,连续数据的值是不确定的,唯一确定的是它在某个区间内),如身高、重量、长度、温度、时间等等。
我相信很多人都会这样想,连续数据是像数数那样是顺着的连续的。事实上它也是。离散数据也可以是顺着的,是不是这样就好难和离散数据区分开了呢?事实上,像上面举的列子中,离散数据1、2、3它们仍然只是数轴上的一些点,还算不上连续。在概率学习中,离散数据的值,都是确定的,每一次随机实验的结果都必定属于某个离散值。而对于适用于连续数据特点的随机实验来说,每一次结果的值都不能够确定,只是知道它所有的区间,如[0,1]这个区间,这一次结果是0,下一次可能是0.1,再下一次可能是0.11,依次下去,结果总是无穷无尽的,虽然是这样了,但是它总发生在[0,1]这个区间中,每次实验的结果,它可以取这个区间的任意值。
均匀分布
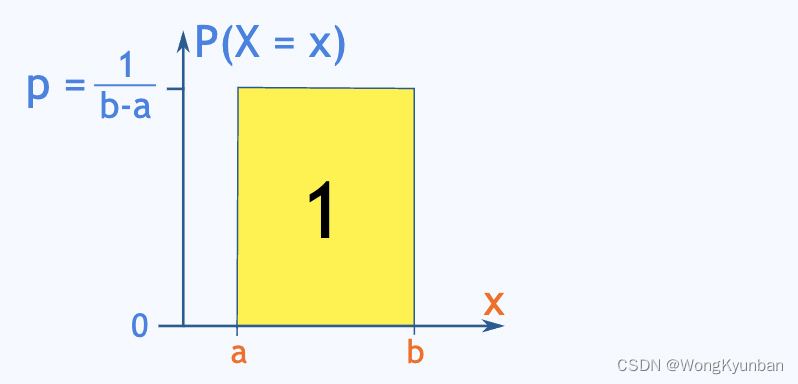
均匀分布是最简单的分布。对[a,b]这个闭区间中的所有值,它们都有相等的概率。由于它们的概率之和为1,那么每个任意值的概率为P=1/(b-a) 。所以,
P(X = x) = 1/(b−a) ,其中 a ≤ x ≤ b,在这个区间以外的值的概率都是0,即P(X = x) = 0 。
我们举个应用的例子,城市广场上的音乐喷泉每隔两小时(120分钟)会开一次,你在任意时刻到达广场并停留半小时(30分钟),那么你可以看到音乐喷泉的概率有多大?
设你在a时刻到,a+30离开,所以你看到的概率就是30/120.
累积均匀分布(Cumulative distribution function,CDF)
我们可以将均匀分布作为累积分布(随其进行而累加)。
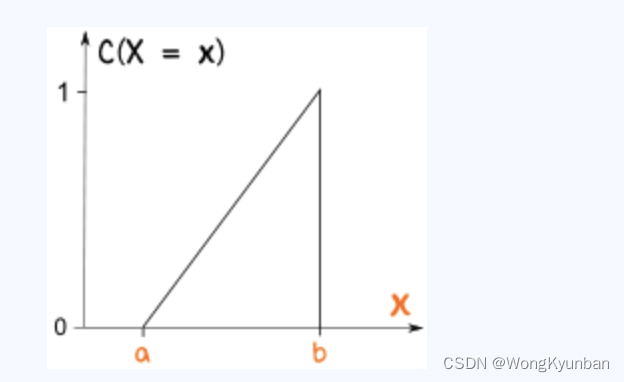
概率从 0 开始,累积到 1 。用这个分布来计算看音乐喷泉的概率,在 a+30 时,概率累积到大约 30/120.
了解并掌握如何使用均匀分布有助于我们处理一些更复杂的分布,这些连续分布有一个通用的名字,那就是概率密度函数(probability density function,PDF) 。
最重要的连续分布是标准正态分布(Standard Normal Distribution) ,它的随机变量用一个它专用的字母Z来表示。
下一篇我们就讲最重要的概率密度函数,即最重要的连续分布------正态分布。