写在前面:
首先感谢兄弟们的订阅,让我有创作的动力,在创作过程我会尽最大能力,保证作品的质量,如果有问题,可以私信我,让我们携手共进,共创辉煌。
路虽远,行则将至;事虽难,做则必成。只要有愚公移山的志气、滴水穿石的毅力,脚踏实地,埋头苦干,积跬步以至千里,就一定能够把宏伟目标变为美好现实。
"相似性度量(similarity measurement)"系列文章:、
【数据挖掘】机器学习中相似性度量方法-欧式距离
【数据挖掘】机器学习中相似性度量方法-余弦相似度
【数据挖掘】机器学习中相似性度量方法-曼哈顿距离
Hello,大家好。
继续更新"相似性度量(similarity measurement)"系列文章,今天介绍的是切比雪夫距离。多的不说,少的不唠,下面开始今天的教程。
以下内容,完全是我根据参考资料和个人理解撰写出来的,不存在滥用原创的问题。

1、切比雪夫距离
切比雪夫距离(Chebyshev Distance)是一种在向量空间或序列空间中计算两个点或序列之间相似度的度量方式。
切比雪夫距离的一个直观理解可以与国际象棋中的"王"的移动方式相联系。在国际象棋中,"王"可以往前后左右以及斜前斜后方向移动一格,因此其移动步数可以看作是棋盘上两个位置之间的切比雪夫距离。
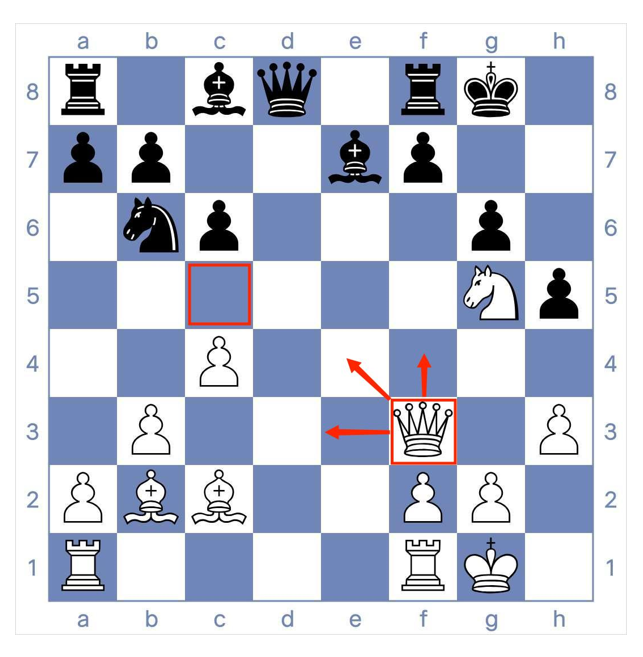
切比雪夫距离与其他距离度量(如欧氏距离、曼哈顿距离)有所不同。它关注的是各维度上差值的最大值,而不是像欧氏距离那样关注各维度上差值的平方和。这使得切比雪夫距离在某些应用场景中具有特殊的优势。
2、计算公式
计算切比雪夫距离时,需要比较两个点或序列中每一对对应位置的元素,并计算它们的差的绝对值。然后从这些差值中取最大值作为切比雪夫距离。例如,对于序列A: [10, 20, 30]和序列B: [5, 10, 20],切比雪夫距离的计算过程为:计算差值 |10 - 5| = 5,|20 - 10| = 10,|30 - 20| = 10,然后取最大值10作为切比雪夫距离。
2.1 二维平面
二维平面两个点A( x 1 , y 1 x_ 1, y_ 1 x1,y1)和B( x 2 , y 2 x_ 2, y_ 2 x2,y2)之间的切比雪夫距离:
d ( A , B ) = m a x ( ∣ x 1 − x 2 ∣ , ∣ y 1 − y 2 ∣ ) \ d(A,B) = max(|x_1 - x_2| , |y_1 - y_2|) d(A,B)=max(∣x1−x2∣,∣y1−y2∣)
2.2 高维空间
两个向量A( x 1 , x 2 , x 3 , . . . , x n x_ 1,x_ 2, x_ 3, ..., x_ n x1,x2,x3,...,xn)和B( y 1 , y 2 , y 3 , . . . , y n y_ 1,y_ 2, y_ 3,..., y_ n y1,y2,y3,...,yn)之间的切比雪夫距离:
d ( A , B ) = m a x ( ∣ x 1 − y 1 ∣ , ∣ x 2 − y 2 ∣ , . . . , ∣ x n − y n ∣ ) \ d(A,B) = max({|x_{1}-y_{1}|,|x_{2}-y_{2}|,...,|x_{n}-y_{n}|}) d(A,B)=max(∣x1−y1∣,∣x2−y2∣,...,∣xn−yn∣)
3、代码实现
编写代码实现切比雪夫距离,下面是Python代码:
py
# -*- coding: utf-8 -*-
"""
Created on Sun Jun 16 22:19:04 2024
@author: AIexplore微信公众号
"""
import numpy as np
def chebyshev_distance(X, Y):
"""
计算两个点(向量)之间的切比雪夫距离。
参数:
X (list or numpy.ndarray): 第一个点的坐标列表或NumPy数组。
Y (list or numpy.ndarray): 第二个点的坐标列表或NumPy数组。
返回:
float: 两个点之间的切比雪夫距离。
"""
# 确保两个点具有相同的维度
assert len(X) == len(Y), "The points must have the same dimension."
# 计算每个维度上的差的绝对值,并取最大值
distance = np.max(np.abs(np.array(X) - np.array(Y)))
return distance
# data
A = [1, 2]
B = [2, 6]
print(chebyshev_distance(A, B)) # 输出应为 4
# data
A = np.array([1, 2, 3])
B = np.array([2, 9, 4])
print(chebyshev_distance(A, B)) # 输出应为 7输出结果:
chebyshev_distance: 4
chebyshev_distance: 74、应用场景
切比雪夫距离越小表示两个序列或两个点之间的差异越小、相似度越高。切比雪夫距离常用于自然语言处理、信息检索和生物信息学等领域,在这些领域中,它常被用来衡量序列之间的差异或相似度。
参考文章
1\]https://blog.csdn.net/weixin_35757704/article/details/115437768 \[2\]https://mp.weixin.qq.com/s/g1-U59Xo7ScjscyrL61Ujw \[3\]https://cloud.tencent.com/developer/article/2281505 \[4\]https://blog.51cto.com/u_12273822/5245220 ## 写在最后 作者介绍:CSDN人工智能领域优质创作者,CSDN博客专家,阿里云专家博主,阿里云技术博主,有机器学习、深度学习、OCR识别项目4年以上工作经验,专注于人工智能技术领域。会根据实际项目不定期输出一些非商业的技术,内容不限,欢迎各位朋友关注。 1、关注下方公众号,让我们共同进步。 2、需要技术指导、交流合作,点击"关于我-与我联系"添加微信交流。 都看到这里了,动动发财的小手点个赞再走吧。 微信扫码关注微信公众号,发现不一样的世界。  